28 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác (Đúng sai - trả lời ngắn) có đáp án
28 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Đẳng thức nào sau đây đúng?
\[\tan \left( {180^\circ - \alpha } \right) = \tan \alpha .\]
\(\cot \left( {180^\circ - \alpha } \right) = - \cot \alpha .\)
\(\cos \left( {180^\circ - \alpha } \right) = \cos \alpha .\)
\(\sin \left( {180^\circ - \alpha } \right) = - \sin \alpha .\)
Giá trị \(\cos 45^\circ + \sin 45^\circ \) bằng bao nhiêu?
\[1\].
\(\sqrt 2 \).
\(\sqrt 3 \).
\[0\].
Tính giá trị của biểu thức \(P = \sin 30^\circ \cos 60^\circ + sin60^\circ cos30^\circ \).
\(P = 1\).
\(P = 0\).
\(P = \sqrt 3 \).
\(P = - \sqrt 3 \).
Giá trị của biểu thức \(A = \tan 1^\circ \tan 2^\circ \tan 3^\circ ...\tan 88^\circ \tan 89^\circ \) là
\(0\).
\(2\).
\(3\).
\(1\).
Cho \(\tan \alpha - \cot \alpha = 3.\) Tính giá trị của biểu thức sau: \(A = {\tan ^2}\alpha + {\cot ^2}\alpha \).
\(A = 12\).
\(A = 11\).
\(A = 13\).
\(A = 5\).
Cho \(\sin \alpha = \frac{4}{5}\)\(\left( {0^\circ < \alpha < 90^\circ } \right)\). Tính \(\cos \alpha \).
\(\cos \alpha = \frac{5}{3}\).
\(\cos \alpha = \frac{3}{5}\).
\(\cos \alpha = - \frac{3}{5}\).
\(\cos \alpha = - \frac{4}{5}\).
Bất đẳng thức nào dưới đây là đúng?
\(\sin 90^\circ < \sin 100^\circ \).
\(\tan 85^\circ < \tan 125^\circ \).
\(\cos 95^\circ > \cos 100^\circ \).
\(\cos 145^\circ > \cos 125^\circ \).
Hệ thức nào sau đây đúng?
\(5\left( {{{\cos }^2}\frac{\alpha }{5} + {{\sin }^2}\frac{\alpha }{5}} \right) = 5.\)
\({\cos ^2}\frac{\alpha }{2} + {\sin ^2}\frac{\alpha }{2} = \frac{1}{2}.\)
\({\cos ^2}\frac{\alpha }{3} + {\sin ^2}\frac{\alpha }{3} = 3.\)
\({\cos ^2}\frac{\alpha }{4} + {\sin ^2}\frac{\alpha }{4} = \frac{1}{4}.\)
Cho \(\sin \alpha = \frac{4}{5}\) với \(90^\circ < \alpha < 180^\circ \). Giá trị của \(\cot \alpha \) là
\(\frac{4}{3}\).
\( - \frac{4}{3}\).
\(\frac{3}{4}\).
\( - \frac{3}{4}\).
Cho \(\cot \alpha = \frac{1}{3}\). Giá trị của biểu thức \(A = \frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}\) là:
\(13\).
\( - \frac{{15}}{{13}}\).
\( - 13\).
\(\frac{{15}}{{13}}\).
Cho \[\Delta ABC\] có \[AB = 5\]; \(\widehat A = 40^\circ \); \(\widehat B = 60^\circ \). Độ dài \[BC\] gần nhất với kết quả nào?
\[3,7\].
\[3,3\].
\[3,5\].
\[3,1\].
Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\)cm, \(AC = 9\)cm. Tính \(\cos A\).
\(\cos A = - \frac{2}{3}\).
\(\cos A = \frac{1}{2}\).
\(\cos A = \frac{1}{3}\).
\(\cos A = \frac{2}{3}\).
Cho \(\Delta ABC\)có góc \(\widehat {BAC} = 60^\circ \) và cạnh \(BC = \sqrt 3 \). Tính bán kính của đường tròn ngoại tiếp \(\Delta ABC\).
\(R = 4\).
\(R = 1\).
\(R = 2\).
\(R = 3\).
Cho tam giác ABC có \(a = 8,b = 10\), góc \(C\) bằng \(60^\circ \). Độ dài cạnh \(c\)là:
\(c = 3\sqrt {21} \).
\(c = 7\sqrt 2 \).
\(c = 2\sqrt {11} \).
\(c = 2\sqrt {21} \).
Phần II. Trắc nghiệm đúng, sai
Cho \(\sin \alpha = \frac{3}{5},\left( {90^\circ < \alpha < 180^\circ } \right)\).
a) \(\cos \alpha > 0\).
b) \({\cos ^2}\alpha = \frac{{16}}{{25}}\).
c) \[\tan \left( {180^\circ - \alpha } \right) = - \frac{3}{4}\].
d) \[A = \frac{{\tan \alpha - \cot \left( {180^\circ - \alpha } \right)}}{{\sin \left( {90^\circ - \alpha } \right)}} = \frac{{125}}{{48}}\].
Cho \(\cot \alpha = - \sqrt 2 ,\left( {0^\circ < \alpha < 180^\circ } \right)\).
a) \(\sin \alpha > 0\).
b) \(\sin \alpha = \pm \frac{1}{{\sqrt 3 }}\).
c) \(\cos \alpha = - \frac{{\sqrt 6 }}{3}\).
d) \(\tan \alpha = \frac{1}{{\sqrt 2 }}\).
Biết \(\tan \alpha = 2\) và \(0^\circ < \alpha < 90^\circ \).
a) \(\cot \alpha = \frac{1}{2}\).
b) \[\sin \alpha \cdot \cos \alpha < 0\].
c) \[\cos \alpha = \frac{1}{{\sqrt 5 }}\].
d) \[\cos \alpha + \sin \alpha = \frac{{2\sqrt 5 }}{5}\].
Cho \(\cos \alpha = - \frac{2}{3}\).
a) \(90^\circ < \alpha < 180^\circ \).
b) \(\cot \alpha \, < \,0\).
c) \(\sin \alpha = - \frac{{\sqrt 5 }}{3}\).
d) \(\tan \alpha = \frac{{\sqrt 5 }}{2}\).
Cho \({\rm{tan}}\alpha = 3\) và \({\rm{0}}^\circ < \alpha < 90^\circ \).
a) \(\cot \alpha = \frac{1}{3}.\)
b) \(\cos \alpha = \frac{{\sqrt {10} }}{{10}}.\)
c) \(5{\sin ^2}\alpha - 3{\cos ^2}\alpha + \cot \left( {90^\circ - \alpha } \right) = \frac{{36}}{7}\).
d) Giá trị của biểu thức \(E = \frac{{{{\sin }^2}\alpha - 5{{\cos }^2}\alpha }}{{2{{\sin }^2}\alpha + 3\sin \alpha \cos \alpha + {{\cos }^2}\alpha }} = \frac{a}{b}\) với \(\left( {a;b} \right) = 1\) và \(a,b\, \in {\mathbb{N}^*}\). Khi đó \[a + b = 8\].
Cho tam giác \(ABC\) có \(b = 7\;\,{\rm{cm}},c = 5\;\,{\rm{cm}},\widehat A = 120^\circ \).
a) \(a = \sqrt {127} \;\,{\rm{cm}}\).
b) \(\cos B \approx 0,21\).
c) \(\cos C \approx 0,91\).
d) \(R \approx 6,03\,{\rm{cm}}\).
Phần III. Trắc nghiệm trả lời ngắn
Cho \(\cot \alpha = - \sqrt 2 \) và \(P = \frac{{2\sin \alpha - \sqrt 2 \cos \alpha }}{{4\sin \alpha + 3\sqrt 2 \cos \alpha }}\). Tính giá trị biểu thức \(A = {m^2} + {n^2}\) biết \(P = \frac{m}{n}\)(\(m \in \mathbb{Z},n \in \mathbb{N}\) và \(\frac{m}{n}\) là phân số tối giản).
Cho góc \(\alpha \,\left( {0^\circ < \alpha < 90^\circ } \right)\) thỏa mãn \(\sin \alpha = \frac{1}{3}\). Tính giá trị biểu thức \[P = \sin \left( {90^\circ - \alpha } \right) - \cos \left( {180^\circ - \alpha } \right)\] (làm tròn kết quả đến hàng phần trăm).
Cho cot \(\alpha = 2\). Khi đó, ta có \(B = \frac{{\sin \alpha + 2\cos \alpha }}{{{{\sin }^3}\alpha - {{\cos }^3}\alpha }} = - \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức \(a - b\).
Tính giá trị của biểu thức: \(F = 1 - 2{\sin ^2}55^\circ + 4{\cos ^2}60^\circ - 2{\sin ^2}35^\circ + \tan 55^\circ \tan 35^\circ \).
Cho \(\tan \alpha = 1\). Tính \(B = \frac{{{{\sin }^2}\alpha + 1}}{{2{{\cos }^2}\alpha - {{\sin }^2}\alpha }}\).
Cho tam giác \(ABC\) có \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và \(a = 10\). Tính chu vi tam giác đó.
Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) biết \(a \ne b\) và \(a\left( {{a^2} - {c^2}} \right) = b\left( {{b^2} - {c^2}} \right)\). Khi đó, số đo của \(\widehat {{\mkern 1mu} C{\mkern 1mu} }\) bằng bao nhiêu độ?
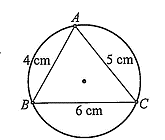
Từ một miếng bìa hình tròn, bạn Nam cắt ra một hình tam giác \(ABC\) có độ dài các cạnh \(AB = 4\;{\rm{cm}},AC = 5\;{\rm{cm}},BC = 6\;{\rm{cm}}\) (Hình vẽ). Tính bán kính \(R\) của miếng bìa ban đầu (làm tròn kết quả đến hàng đơn vị theo đơn vị centimét).