28 câu hỏi
Trong phát biểu sau đây, phát biểu nào đúng?
Hình chóp có tất cả các mặt là hình tam giác
Tất cả các mặt bên của hình chóp là hình tam giác
Tồn tại một mặt bên của hình chóp không phải là hình tam giác
Số cạnh bên của hình chóp bằng số mặt của nó
Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
Ba điểm mà nó đi qua
Một điểm và một đường thẳng thuộc nó
Ba điểm không thẳng hàng
Hai đường thẳng thuộc mặt phẳng
Trong các phát biểu sau, phát biểu nào đúng?
Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng có thể có đúng hai điểm chung
Nếu hai mặt phẳng có một điểm chung thì chúng có chung một đường thẳng duy nhất hoặc mọi điểm thuộc mặt phẳng này đều thuộc mặt phẳng kia.
Hai mặt phẳng luôn có điểm chung.
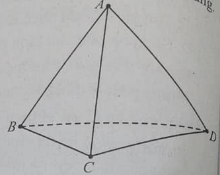
Cho hình tứ diện ABCD, phát biểu nào sau đây là đúng?
AC và BD cắt nhau
AC và BD không có điểm chung
Tồn tại một mặt phẳng chứa AD và BC
AB và CD song song với nhau
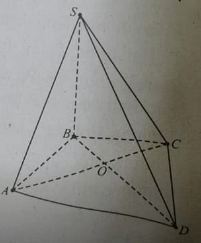
Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
Giao tuyến của (SAC) và (SBD) là SO.
Giao tuyến của (SAB) và (SCD) là điểm S.
Giao tuyến của (SBC) và (SCD) là SK, với K là giao điểm của SD và BC.
Giao tuyến của (SOC) và (SAD) là SM, với M là giao điểm của AC và SD.
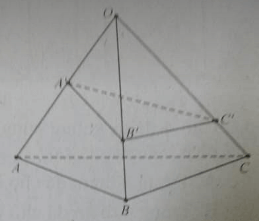
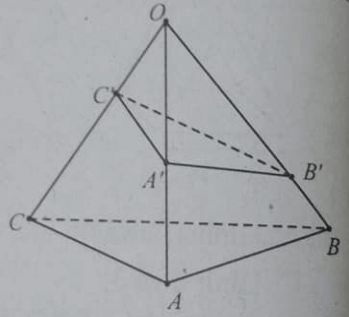
Cho hình chóp O.ABC, A’ là trung điểm của OA; các điểm B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng.
Giao tuyến của (OBC) và (A’B’C’) là A’B’;
Giao tuyến của (ABC) và (OC’A’) là CK, với K là giao điểm của C’B’ với CB
(ABC) và (A’B’C’) không cắt nhau
Giao tuyến của (ABC) và (A’B’C’) là MN, với M là giao điểm của AC và A’C’, N là giao điểm của BC và B’C’.
Trong các phát biểu sau, phát biểu nào đúng?
Hình tứ diện có 4 cạnh
Hình tứ diện có 4 mặt
Hình tứ diện có 6 đỉnh
Hình tứ diện có 6 mặt
Số cạnh của hình chóp tam giác là:
5
4
6
3
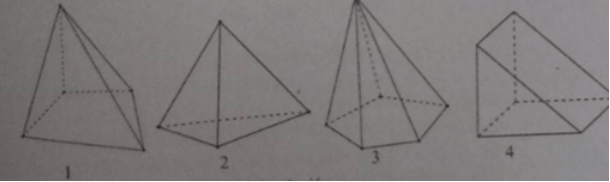
Hình biểu diễn nào sau đây vẽ đúng hình chóp?
Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
Trong 4 điểm đã cho không có ba điểm nào thẳng hàng
Trong 4 điểm đã cho luôn luôn tồn tại 3 điểm thẳng hàng
Số mặt phẳng đi qua 3 trong 4 điểm đã cho là 4
Số đoạn thẳng nối hai điểm trong 4 điểm đã cho là 6.
Có duy nhất một mặt phẳng đi qua
Hai đường thẳng
Một điểm và một đường thẳng
Ba điểm
Hai đường thẳng cắt nhau
Có một và chỉ một mặt phẳng đi qua
Ba điểm
Một điểm và một đường thẳng không chứa điểm đó.
Hai điểm
Bốn điển
Hai đường thẳng chéo nhau nếu.
Chúng không có điểm chung
Chúng không cắt nhau và không song song với nhau
Chúng không cùng nằm trong bất kì một mặt phẳng nào
Chúng không nằm trong bất cứ hai mặt phẳng nào cắt nhau.
Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
1
2
3
4
Cho 6 đường thẳng đôi một cắt nhau. Hỏi xác định được nhiểu nhất bao nhiêu mặt phẳng đi qua 2 trong số các đường thẳng đã cho
6
8
12
15
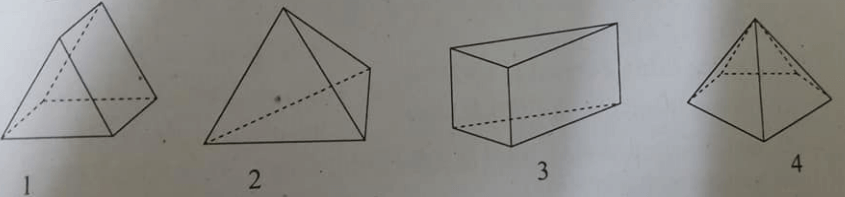
Trong các hình sau, hình nào là hình chóp.
Hình 1,2 và 4
hình 2 và 4
hình 2 và 3
tất cả các hình trên.
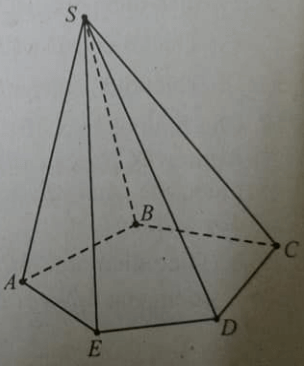
Cho hình chóp S.ABCDE, phát biểu nào sau đây là đúng.
Điểm B thuộc mặt phẳng (SED)
Điểm E thuộc mặt phẳng (SAB)
Điểm D thuộc mặt phẳng (SBC)
Điểm B thuộc mặt phẳng (SAB)
Phát biểu nào sau đây là đúng?
Hình 1 và hình 4 là các hình chóp tứ giác
Hình 2 và hình 4 là các hình chóp tam giác
Hình 1,2,3 là các hình chóp
Hình 3,4 không phải là hình chóp.
Cho hình chóp S.ABCDE, phát biều nào sau đây là đúng?
SE và AB cắt nhau
Đường thẳng SB nằm trong mặt phẳng SED
(SAE) và (SBC) có một điểm chung duy nhất
SD và BC chéo nhau.
Cho hình chóp O.ABC, A’ là trung điểm của OA, B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng?
Đường thẳng AC và A’C’ cắt nhau.
Đường thẳng OA và C’B’ cắt nhau.
Hai đường thẳng AC và A’C’ cắt nhau tại một điểm thuộc (ABO)
Hai đường thẳng CB và C’B’ cắt nhau tại một điểm thuộc (OAB)
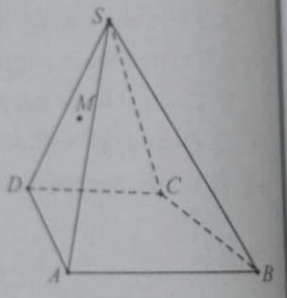
Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?
Giao điểm của (SMC) với BD là giao điểm của CN với BD, trong đó N là giao điểm của SM và AD.
Giao điểm của (SAC) với BD là giao điểm của SA và BD
Giao điểm của (SAB) với CM là giao điểm của SA và CM
Đường thẳng DM không cắt mặt phẳng (SBC)
Cho hình chóp S.ABCD, các điểm A’, B’, C’ lần lượt thuộc các cạnh SA, SB, SC. Phát biểu nào sau đây là đúng?
Thiết diện của (A’B’C’) với hình chóp S.ABCD là tam giác A’B’C’
Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D’ với D’ là giao điểm của B’I với SD, trong đó I là giao điểm của A’C’ với SO, O là giao điểm của AC và BD
Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác SA’B’C’
Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D
Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây là đúng?
Giao điểm của MN với (SBD) là giao điểm của MN với BD.
Đường thẳng MN không cắt mặt phẳng (SBD)
Giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao điểm của CM với BD
Giao điểm của MN với (SBD) là M.
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?
Thiết diện của (MND) với hình chóp là tam giác MND
Thiết diện của (MND) với hình chóp là tứ giác NDMK, với K là giao điểm của SB với NI, I là giao điểm của MD với BC
Thiết diện của (MND) với hình chóp là tứ giác NDMB
Thiết diện của (MND) với hình chóp là tam giác NDB.
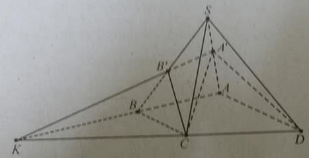
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
Hình vẽ như sau:
Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tam giác A’B’C.
Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’BCD
Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’B’CA
Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’B’CD
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
Ba đường thẳng A’B’, AB, CD đồng quy
Ba đường thẳng A’B’, AB, CD đồng quy hoặc đôi một song song
Trong ba đường thẳng A’B’, AB, CD có hai đường thẳng không thể cùng thuộc một mặt phẳng.
Ba đường thẳng A’B’, AB, CD đồng quy tại điểm thuộc mặt phẳng (SBC).
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. số giao điểm của ba đường thẳng là:
3
6
1
kết quả khác
Thiết diện của mặt phẳng với tứ diện
Tam giác hoặc tứ giác
Luôn là một tứ giác
Luôn là một tam giác
Tam giác hoặc tứ giác hoặc ngũ giác