27 câu hỏi
Một chất điểm chuyển động theo quy luật \(s\left( t \right) = {t^2} - \frac{1}{6}{t^3}\left( m \right).\) Tìm thời điểm \(t\) (giây) mà tạo đó vận tốc \(v\left( {m/s} \right)\) của chuyển động đạt giá trị lớn nhất.
\(t = 2\).
\(t = 0,5\).
\(t = 2,5\).
\(t = 1\).
Công suất \(P\)(đơn vị \[W\]) của một mạch điện được cung cấp bởi một nguồn pin \(12V\)được cho bởi công thức \(P = 12I - 0,5{I^2}\) với \(I\)(đơn vị \(A\)) là cường độ dòng điện. Tìm công suất tối đa của mạch điện.
\(72\).
\(12\).
\( - \frac{1}{{192}}\).
\(\frac{{23}}{2}\).
Một vật chuyển động theo quy luật \(s = - 2{t^3} + 24{t^2} + 9t - 3\) với \(t\) là khoảng thời gian tính từ lúc bắt đầu chuyển động và \(s\) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
289 \(\left( {m/s} \right)\).
105 \(\left( {m/s} \right)\).
111 \(\left( {m/s} \right)\).
487 \(\left( {m/s} \right)\).
Độ giảm huyết áp của một bệnh nhân được đo bởi công thức \(G\left( x \right) = 0,25{x^2}\left( {30 - x} \right)\) trong đó \(x\left( {mg} \right)\) và là lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng bao nhiêu:
15mg
30mg
40mg
20mg
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là \(G\left( t \right) = 45{t^2} - {t^3}\), (kết quả khảo sát được trong 10 tháng vừa qua). Nếu xem \(G'\left( t \right)\) là tốc độ truyền bệnh (người / ngày) tại thời điểm t thì tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ:
25
30
20
15
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. độ sâu \(h\left( m \right)\) của mực nước trong kênh tính theo thời gian \(t\left( h \right)\) trong ngày cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + \frac{\pi }{3}} \right) + 12\). Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
\(t = 10\left( h \right)\)
\(t = 14\left( h \right)\)
\(t = 15\left( h \right)\)
\(t = 22\left( h \right)\)
Thể tích nước của một bề bơi sau t phút b ơm tính theo công thức \(V\left( t \right) = \frac{1}{{100}}\left( {30{t^3} - \frac{{{t^4}}}{4}} \right)\) \(\left( {0 \le t \le 90} \right)\). Tốc độ bơm nước tại thời điểm t được tính bởi \(v\left( t \right) = V'\left( t \right)\). Trong các khẳng định sau, khẳng định nào đúng.
Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
Tốc độ bơm luôn giảm.
Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
Cả ba đáp án đều sai
Khi nuối cá thí nghiệm trong hồ, một nhà khoa học đã nhận thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng là \(P\left( n \right) = 480 - 20n\left( g \right)\). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
14
13
12
11
Để giảm nhiệt độ trong phòng từ \({28^0}C\), một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi \(T\) (đơn vị \(^0C\)) là nhiệt độ phòng ở phút thứ \(t\) được cho bởi công thức \(T = - 0,008{t^3} - 0,16t + 28\) với \(t \in [1;10]\). Tìm nhiệt độ thấp nhất trong phòng đạt được trong thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động.
\({27,832^0}C\).
\({18,4^0}C\).
\({26,2^0}C\).
\({25,312^0}C\).
Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng mỗi tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ 100.000 đồng mỗi tháng thì có thêm 2 căn hộ bị bỏ trống. Muốn có thu nhập cao nhất, công ty đó phải cho thuê với giá mỗi căn hộ là bao nhiêu?
2.250.000
2.350.000
2.450.000
2.550.000
Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
44.000đ
43.000đ
42.000đ
41.000đ
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa được là 60 hành khách một chuyến. Nếu một chuyến chở được m hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận mỗi chuyến xe là lớn nhất.?
30
40
50
60
Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
480 ngàn.
50 ngàn.
450 ngàn.
80 ngàn.
Công ty dụ lịch Ban Mê dự định tổ chức một tua xuyên Việt. Công ty dự định nếu giá tua là 2 triệu đồng thì sẽ có khoảng 150 người tham gia. Để kích thích mọi người tham gia, công ty quyết định giảm giá và cứ mỗi lần giảm giá tua 100 ngàn đồng thì sẽ có thêm 20 người tham gia. Hỏi công ty phải bán giá tua là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất.
1375000.
3781250.
2500000.
3000000.
Bác Tôm có một cái ao có diện tích \(50{{\rm{m}}^{\rm{2}}}\) để nuôi cá. Vụ vừa qua bác nuôi với mật độ \(20\,{\rm{con/}}{{\rm{m}}^{\rm{2}}}\) và thu được tất cả \(1,5\) tấn cá thành phẩm. Theo kinh nghiệm nuôi cá thu được bác ấy cứ giảm đi \(8\) con/m2 thì tương ứng sẽ có mỗi con cá thành phẩm thu được tăng thêm \(0,5\,{\rm{kg}}{\rm{.}}\) Hỏi vụ tới bác phải mua bao nhiêu con cá giống để đạt được tổng khối lượng cá thành phẩm cao nhất? (Giả sử không có hao hụt trong quá trình nuôi).
\(1100\) con.
\(1000\) con.
\(500\) con.
\(502\) con.
Một màn ảnh hình chữ nhật cao 1,4 mét và đặt ở độ cao 1,8 mét so với tầm mắt (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đó? Biết rằng góc \(\widehat {BOC}\) là góc nhọn.
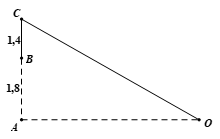
\(AO = 2,4\)m
\(AO = 2\)m
\(AO = 2,6\)m
\(AO = 3\)m
Từ hình vuông có cạnh bằng \(6\) người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Tính thể tích lớn nhất của khối hộp.
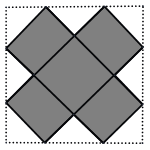
\(8\sqrt 2 \).
\(10\sqrt 2 \).
\(9\sqrt 2 \).
\(11\sqrt 2 \).
Cho hình vuông \(ABCD\) có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với \(ABCD\). Biết rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác cân nhỏ nhất bằng bao nhiêu?
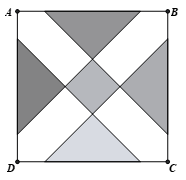
\(\frac{{19}}{3}\).
\(\frac{{17}}{3}\).
\(\frac{{16}}{3}\).
\(\frac{{14}}{3}\).
Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất?Biết dòng sông là thẳng,mục tiêu cách chiến sỹ 1km theo đường chim bay và chiến sỹ cách bờ bên kia 100m.
\[\frac{{200\sqrt 2 }}{3}\].
\[75\sqrt 3 \].
\[\frac{{200\sqrt 3 }}{3}\].
\[75\sqrt 2 \].
Một người dự định làm một bể chứa nước hình trụ bằng inốc có nắp đậy với thể tích \(1\) (m3). Chi phí mỗi m2 đáy là \(600\) nghìn đồng, mỗi m2 nắp là \(200\) nghìn đồng và mỗi m2 mặt bên là \(400\) nghìn đồng. Hỏi người đó án kính bể là bao nhiêu để chi phí làm bể ít nhất?
\(\sqrt[3]{{2\pi }}\).
\(\sqrt[3]{{\frac{1}{2}}}\).
\(\sqrt[3]{{\frac{1}{{2\pi }}}}\).
\(\sqrt[3]{{\frac{1}{\pi }}}\).
Một khúc gỗ tròn hình trụ cần xẻ thành một chiếc xà có tiết diện ngang là hình vuông và 4 miếng phụ như hình vẽ. Hãy xác định kích thước của các miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. Biết đường kính khúc gỗ là \(d\).
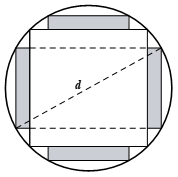
Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{16}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{15}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{14}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{13}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Nhà Long muốn xây một hồ chứa nước có dạng một khối hộp chữ nhật có nắp đậy có thể tích bằng \(576{m^3}\). Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá tiền thuê nhân công để xây hồ tính theo \({m^2}\) là \(500.000\) đồng/m2. Hãy xác định kích thước của hồ chứa nước sao cho chi phí thuê nhân công là ít nhất và chi phí đó là bao nhiêu?
Rộng 6m, dài 12m, cao 8m. Tiền: 216 triệu
Rộng 6m, dài 12m, cao 8m. Tiền: 215 triệu
Rộng 6m, dài 12m, cao 8m. Tiền: 214 triệu
Rộng 6m, dài 12m, cao 8m. Tiền: 213 triệu.
Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(R\), nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp?
\(2{R^2}\)
\(5{R^2}\)
\({R^2}\)
\(3{R^2}\)
Để thiết kế một chiếc bể cá hình chữ nhật có chiều cao là \(60cm,\) thể tích là \(96.000c{m^3}\), người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70.000 đồng/m2 và loại kính để làm mặt đáy có giá thành là 100.000 đồng/m2. Chi phí thấp nhất để hoàn thành bể cá là:
\(83.200.000\) đồng
382.000 đồng
83.200 đồng
8.320.000 đồng.
Ông Nam cần xây dựng một bể nước mưa có thể tích \(V = 8\left( {{m^3}} \right)\) dạng hình hộp chữ nhật với chiều dài gấp \(\frac{4}{3}\) lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980.000đ\(/{m^2}\) và ở nắp để hở một khoảng hình vuông có diện tích bằng \(\frac{2}{9}\) diện tích nắp bể. Tính chi phí thấp nhất mà ông Nam phải chi trả (làm tròn đến hàng nghìn đồng).
\[22.770.000\]đ.
\[27.657.000\]đ.
\[20.965.000\]đ.
\[23.235.000\]đ.
Dùng một dây thép dài \(60\)m uốn thành một khung có dạng như hình vẽ. Biết phần dưới là hình chữ nhật và phía trên là một tam giác đều. Diện tích lớn nhất của khung có giá trị bằng:
\[\frac{{900}}{{6 - \sqrt 3 }}\left( {{{\rm{m}}^2}} \right)\].
\[\frac{{1200}}{{6 - \sqrt 3 }}\left( {{{\rm{m}}^2}} \right)\].
\[\frac{{700}}{{3 + \sqrt 3 }}\left( {{{\rm{m}}^2}} \right)\].
\[\frac{{600}}{{3 - \sqrt 3 }}\left( {{{\rm{m}}^2}} \right)\].
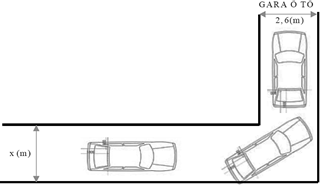
Hình vẽ bên dưới mô tả đoạn đường đi vào GARA Ô TÔ nhà cô Hiền. Đoạn đường đầu tiên có chiều rộng bằng \(x\;({\rm{m}})\), đoạn đường thẳng vào cổng GARA có chiều rộng \(2,6\;({\rm{m}})\). Biết kích thước xe ô tô là \(5{\rm{m}} \times 1,9{\rm{m}}\). Để tính toán và thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước chiều dài \(5\;({\rm{m}})\), chiều rộng \(1,9\;({\rm{m}})\). Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để ô tô có thể đi vào GARA được?
\(x = 3,7\;({\rm{m}})\).
\(x = 2,6\;({\rm{m}})\).
\(x = 3,55\;({\rm{m}})\).
\(x = 4,27\;({\rm{m}})\).
