15 CÂU HỎI
Bài tập cuối chương I
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) có bảng biến thiên như sau:
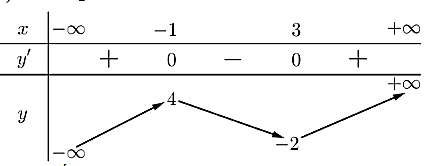
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−2; 4).
(−2; +∞).
(−1; 3).
(−∞; −1).
Cho hàm số y = f(x) liên tục trên ℝ, có đạo hàm f'(x) = (2x + 1)(x – 3)2(x – 2)3 với mọi x Î ℝ. Số điểm cực đại của hàm số y = f(x) là
0.
1.
2.
3.
Giá trị nhỏ nhất của hàm số f(x) = x3 – 3x + 2 trên đoạn [−3; 3] bằng
−16.
20.
0.
4.
Tiệm cận đứng của đồ thị hàm số 
là
A. 
.
y = 4
x = 4.
x = 1.
Cho hàm số y = f(x) có đồ thị là đường cong như hình bên dưới
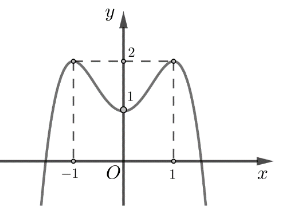
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(0; 1).
(−∞; 0).
(1; +∞).
(−1; 0).
Cho hàm số f(x) liên tục trên đoạn [−2; 3] có đồ thị như hình vẽ dưới đây
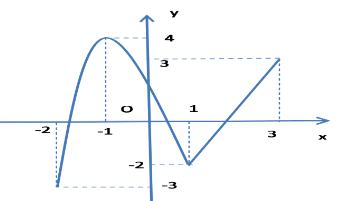
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2; 3]. Giá trị của 2m – 3M bằng
−13.
−18.
−16.
−15.
Cho hàm số f(x) liên tục trên ℝ\{1} và có bảng biến thiên như sau
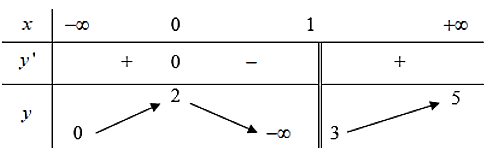
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
4.
1.
3.
2.
Đồ thị sau là đồ thị của hàm số nào?
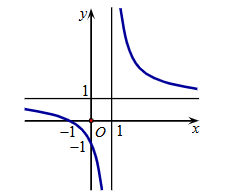
A. 
.
B. 
.
C. 
.
D. 
.
Đồ thị như hình bên dưới là đồ thị của hàm số nào?
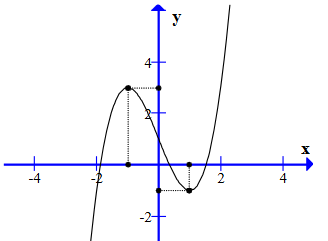
y = −x3 + 3x2 + 1.
y = x3 – 3x – 1.
y = x3 – 3x + 1.
y = −x3 – 3x2 – 1.
Tiệm cận xiên của đồ thị hàm số 
là
y = −2.
y = 1.
y = x + 2.
y = x.
Cho hàm số 
có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
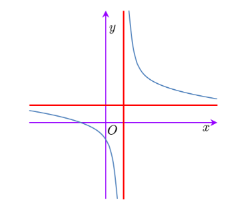
ac > 0, bd > 0.
ab < 0, cd < 0.
ac > 0, cd < 0.
bd < 0, ad > 0.
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ. Hàm số f'(x) có đồ thị như hình bên
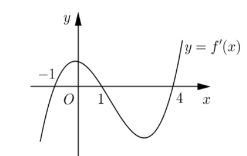
Hàm số y = f(x) đồng biến trên khoảng
(−1; 1).
(−1; 2024).
(−∞; −1).
(1; +∞).
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên như hình
Mệnh đề nào sau đây sai?
Hàm số có hai cực trị.
Phương trình y' = 0 có 2 nghiệm.
Phương trình y = 0 có 2 nghiệm dương và 1 nghiệm âm.
Giá trị cực đại của hàm số là 3.
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau:
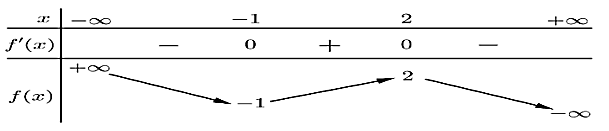
Số đường tiệm cận của đồ thị hàm số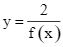 
là
5.
4.
3.
2.
Cho hàm số f(x) có đạo hàm là f'(x) =3x2 + ex. Giá trị lớn nhất của hàm số f(x) trên [0; 2] là:
f(2).
f(0).
f(1).
12 + e2.