25 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài tập cuối chương 1 (Đúng sai - Trả lời ngắn) có đáp án
39 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm f'(x) như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; −2).
(1; +∞).
(−2; 1).
(−2; +∞).
Cho hàm số y = f(x) có đồ thị như hình vẽ
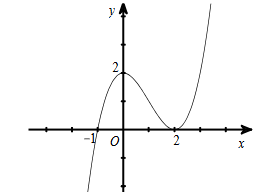
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−∞; −1).
(2; +∞).
(−1; 2).
(0; 2).
Cho hàm số y = f(x) có bảng biến thiên như sau
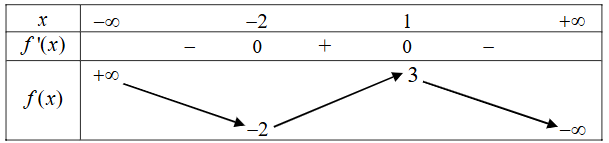
Hàm số y = f(x) đạt cực đại tại điểm
x = −2.
x = 1.
x = 3.
x = 2.
Cho hàm số y = f(x) có đồ thị như hình vẽ
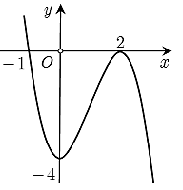
Giá trị cực tiểu của hàm số bằng
−1.
−4.
0.
2.
Điểm cực tiểu của đồ thị hàm số y = −x3 + 3x2 – 4 là
x = 0.
y = −4.
M(0; −4).
N(2; 0).
Cho hàm số f(x) liên tục trên [−1; 5] và có đồ thị trên đoạn [−1; 5] như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [−1; 5]. Tính M + m.
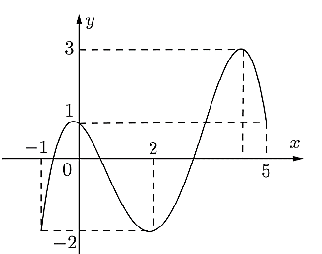
T = −1.
T = 4.
T = 1.
T = 2.
Giá trị nhỏ nhất của hàm số f(x) = x3 – 21x trên đoạn [2; 4] bằng
−38.
B. 
.
−20.
−34.
Tiệm cận đứng của đồ thị hàm số 
là đường thẳng
x = −1.
x = 2.
y = 2.
y = −1.
Tiệm cận ngang của đồ thị hàm số 
là đường thẳng
y = 2.
y = 5.
x = −1.
x = 1.
Cho hàm số y = f(x) có bảng biến thiên như sau
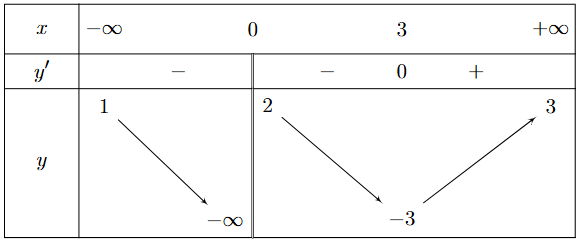
Hỏi đồ thị của hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
4.
1.
2.
3.
Cho hàm số y = f(x) liên tục và nghịch biến trên [1; 3]. Khẳng định nào sau đây đúng?
Giá trị lớn nhất của hàm số y = f(x) trên [1; 3] là f(3).
Giá trị nhỏ nhất của hàm số y = f(x) trên [1; 3] là f(2).
Giá trị lớn nhất của hàm số y = f(x) trên [1; 3] là f(1).
Giá trị nhỏ nhất của hàm số y = f(x) trên [1; 3] là f(1).
Hàm số nào dưới đây có đồ thị như đường cong trong hình vẽ?
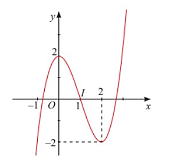
y = x3 + 3x + 2.
y = −x3 + 3x2 + 2.
y = x3 – 3x2 + 2.
y = x3 – 3x2 – 2.
Hàm số nào dưới đây có đồ thị như đường cong trong hình vẽ?
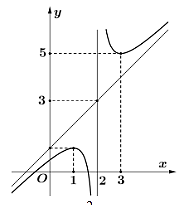
A. 
.
B. 
.
C. 
.
y = −x3+ 3x2+ 1.
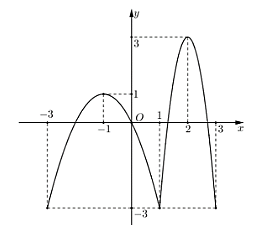
Cho hàm số y = f(x) có đồ thị là đường cong như hình vẽ dưới
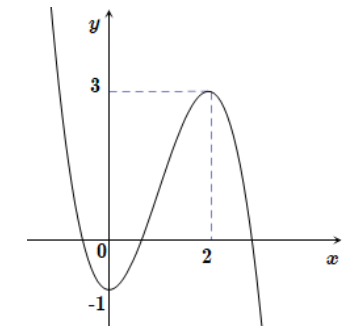
Số nghiệm của phương trình f(x) = −1 bằng
0.
1.
2.
3.
Cho hàm số y = f(x) có đạo hàm f'(x) = (x – 2)(1 – x)2 với mọi x Î ℝ. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(1; +∞).
(2; +∞).
(−∞; 1).
(1; 2).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
a) Hàm số có hai giá trị cực trị là −1 và 3.
Hàm số y = f(x) đồng biến trên khoảng (1; 3)
c) Giá trị lớn nhất của hàm số trên nửa khoảng (1; 3] bằng −2
d) Đồ thị hàm số y = f(x) có tiệm cận đứng x = 1
a) Hàm số y = f(x) đồng biến trên khoảng (−∞; −2).
b) Hàm số y = f(x) đạt cực tiểu tại điểm x = 1
c) Giá trị nhỏ nhất của hàm số trên [−2; 2] bằng f(1)
d) Hàm số y = f(x) có hai điểm cực trị.
a) Khi giá cho thuê mỗi căn hộ là 2 200 000 đồng thì có 10 căn hộ bị trống.
b) Khi giá cho thuê mỗi căn hộ là 2 700 000 đồng thì thu nhập của công ty cao nhất.
c) Thu nhật cao nhất của công ty đạt được là 312 500 000 đồng.
d) Khu thu nhập công ty cao nhất thì số căn hộ có người thuê là 125 căn hộ.
a) Đồ thị (C) có tiệm cận xiên là y = −x – 6
b) Đồ thị (C) nhận điểm I(3; −9) làm tâm đối xứng
c) Hàm số y = f(x) đồng biến trên khoảng (3; 7)
d) Đồ thị (C) có hai điểm cực trị nằm về hai phía đối với Oy.
a) Chiều cao của bể nước là 
(m).
b) Diện tích các mặt cần xây là 
(m2).
c) Chi phí vật liệu thấp nhất khi x = 2 (m).
PHẦN III. TRẢ LỜI NGẮN
Một chất điểm chuyển động có vận tốc tức thời v(t) phụ thuộc vào thời gian t theo hàm số v(t) = t4 – 8t2 + 243 (m/s). Trong khoảng thời gian từ t = 0 (s) đến t = 6 (s) chất điểm đạt vận tốc nhỏ nhất bằng bao nhiêu?
Trong một thí nghiệm y học, người ta cấy 1000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức 
, trong đó t là thời gian tính bằng giây (t ≥ 0). Tại thời điểm t = a (giây) số lượng vi khuẩn nhiều nhất . Giá trị của a bằng?
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp có thể tích bằng 1 m3. Chiều cao của bể là 5 dm, các kích thước khác là x (m), y(m) với x > 0, y > 0. Diện tích toàn phần của bể (không kể nắp) là một hàm số S(x) trên khoảng (0; +∞). Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a2 + b2.
Cho hàm số y = f'(x) có đồ thị như hình vẽ bên dưới. Giá trị lớn nhất của hàm số y = f(x) trên đoạn [−1; 1] là f(x0). Tìm x0.
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 1)(x – 4) với mọi x ∈ ℝ.
Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?