25 câu trắc nghiệm Toán 12 Cánh diều Bài tập cuối chương 1 (Đúng sai - Trả lời ngắn) có đáp án
40 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) có đồ thị là đường cong trong hình.
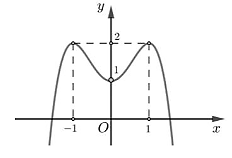
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; 0).
(0; 1).
(1; +∞).
(−1; 0).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau
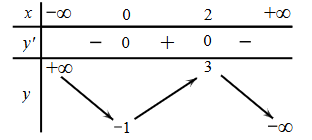
Mệnh đề nào dưới đây sai?
Hàm số nghịch biến trên khoảng (2; +∞).
Hàm số nghịch biến trên khoảng (−∞; 0).
Hàm số đồng biến trên khoảng (−1; 3).
Hàm số đồng biến trên khoảng (0; 2).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu của y' như sau:
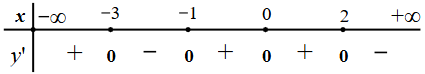
Hàm số y = f(x) có bao nhiêu điểm cực đại?
4.
2.
1.
3.
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ
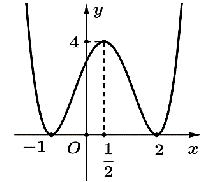
Đồ thị hàm số y = f(x) đạt cực đại tại điểm nào sau đây?
(−1; 2).
B.
.
C. 
.
(0; 4).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau
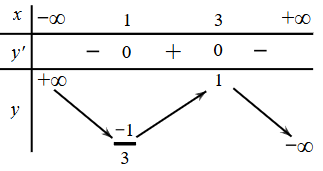
Tìm giá trị lớn nhất của hàm số y = f(x) trên đoạn [2; 4].
2.
3.
1.
4.
Giá trị lớn nhất của hàm số y = −x4 + 3x2 + 1 trên [0; 2] là
1.
29.
C. 
.
−3.
Giá trị nhỏ nhất của hàm số f(x) = x3 – 3x + 2 trên khoảng (0; +∞) bằng
0.
−2.
4.
2.
Cho hàm số y = f(x) có đồ thị (C) là đường cong trong hình sau:
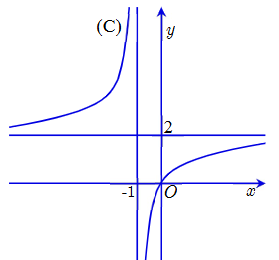
Đường tiệm cận đứng của đồ thị (C) có phương trình là
y = 2.
x = −1.
y = −1.
x = 2.
Cho hàm số y = f(x) có bảng biến thiên như sau:
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận ngang?
0.
2.
3.
1.
Tiệm cận xiên của đồ thị hàm số 
là đường thẳng có phương trình?
y = −x – 1.
y = x – 1.
y = −x + 1.
y = x + 1.
Đường cong ở hình sau là đồ thị của hàm số nào?
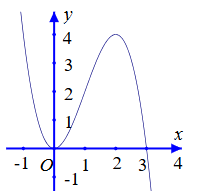
y = −x3 + 3x.
y = −x3+ 3x2.
y = x3–3x.
y = x3–3x2.
Hàm số nào sau đây có bảng biến thiên như hình
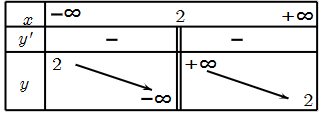
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị là đường cong như hình vẽ
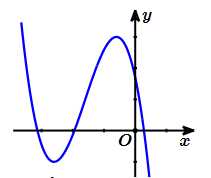
Có bao nhiêu số dương trong các số a, b, c, d?
1.
3.
2.
4.
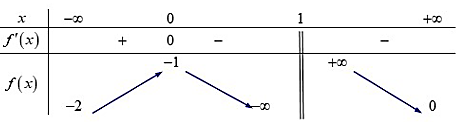
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ
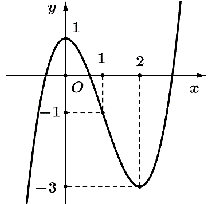
Số nghiệm của phương trình f(x) + 2 = 0.
1.
3.
2.
4.
Cho hàm số y = f(x) xác định và liên tục trên ℝ, có bảng biến thiên như sau
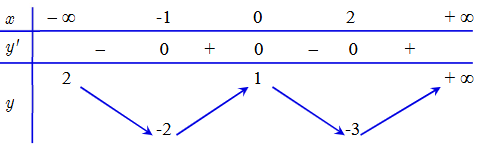
Hỏi đồ thị hàm số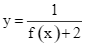 
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
4.
5.
6.
3.
a) Hàm số y = f(x) có 2 điểm cực trị.
b) Hàm số y = f(x) có 1 điểm cực trị
c) Hàm số y = f(x) nghịch biến trên khoảng (−∞; 1).
d) f(2024) > f(2025).
a) Điểm cực tiểu của hàm số là x = 1.
b) Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số, điểm C(−1; 2). Khi đó diện tích tam giác ABC là 12.
c) Hàm số đồng biến trên khoảng (−1;1).
d) Giả sử hàm số đã cho có hai điểm cực trị là x1; x2. Khi đó giá trị x1.x2 = −1.
a)Nếu một mặt hàng với giá 5 nghìn đồng/kg thì khối lượng mặt hàng đó mà cửa tiệm bán được trong một ngày là 20 kg.
b) Công thức biểu diễn R theo p là R = −2p2 + 30p với p > 0.
c) Để một mặt hàng có doanh thu tối thiểu là 88 nghìn đồng, thì giá của mặt hàng đó p ³ 4 nghìn đồng/kg.
d) Giá bán mỗi kg sản phẩm để đạt được doanh thu cao nhất là 7,5 nghìn đồng và doanh thu cao nhất khi đó là 121,5 nghìn đồng.
a) Hàm số y = f(x) đồng biến trên khoảng (−∞; −2).
b) Hàm số y = f(x) đạt cực tiểu tại điểm x = 1.
c) Giá trị nhỏ nhất của hàm số trên [−2; 2] bằng f(1).
d) Hàm số y = f(x) có hai điểm cực trị.
a) Khi giá cho thuê mỗi căn hộ là 2 200 000 đồng thì có 10 căn hộ bị trống.
b) Khi giá cho thuê mỗi căn hộ là 2 700 000 đồng thì thu nhập của công ty cao nhất.
c) Thu nhật cao nhất của công ty đạt được là 312 500 000 đồng.
d) Khu thu nhập công ty cao nhất thì số căn hộ có người thuê là 125 căn hộ.
PHẦN III. TRẢ LỜI NGẮN
Sau khi tiêm một loại thuốc vào cơ thể bệnh nhân, nồng độ thuốc trong máu (tính theo mg/cm3) thay đổi theo công thức 
, trong đó t là thời gian (tính theo giờ) kể từ thời điểm tiêm thuốc, t ³ 0. Nồng độ thuốc trong máu đạt giá trị lớn nhất là bao nhiêu mg/cm3 (kết quả làm tròn đến hàng phần trăm).
Chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1000 và R(x)= 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra. Biết hàm lợi nhuận trung bình 
. Hỏi lợi nhuận trung bình sẽ không vượt quá bao nhiêu triệu động?
Một trang trại rau sạch ở Đà Lạt mỗi ngày thu hoạch được 1 tấn rau. Mỗi ngày, nếu giá bán rau là 30 000 đồng/kg thì bán hết rau, nếu giá bán rau tăng 1000 đồng/kg thì số rau thừa tăng 20 kg. Số rau thừa này được thu mua hết để làm thức ăn chăn nuôi với giá 2000 đồng/kg. Hỏi để mỗi ngày thu được số tiền bán rau lớn nhất thì trang trại đó nên bán rau với giá bao nhiêu nghìn đồng?
Một chất điểm chuyển động có vận tốc tức thời v(t) phụ thuộc vào thời gian t theo hàm số v(t) = t4 – 8t2 + 243 (m/s). Trong khoảng thời gian từ t = 0 (s) đến t = 6 (s) chất điểm đạt vận tốc nhỏ nhất bằng bao nhiêu?
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp có thể tích bằng 1 m3. Chiều cao của bể là 5 dm, các kích thước khác là x (m), y(m) với x > 0, y > 0. Diện tích toàn phần của bể (không kể nắp) là một hàm số S(x) trên khoảng (0; +∞). Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a2 + b2.