24 bài tập Phương trình quy về phương trình bậc nhất có lời giải
24 câu hỏi
Trong các phương trình sau, phương trình nào là phương trình tích
\(\left( {2x + 1} \right)\left( {x - 2} \right) = 1\)
\(x\left( {x - 2} \right) + \left( {6x + 5} \right)\left( {x + 1} \right) = 0\)
\(x - 5 = - 2x + 3\)
\(\left( {x + 4} \right)\left( {5 - 2x} \right) = 0\)
Phương trình \(5\left( {x + 2} \right)\left( {2x - 1} \right) = 0\) có mấy nghiệm
1
2
3
Vô nghiệm
Tất cả các nghiệm của phương trình \(\left( {x - 3} \right)\left( {2x + 4} \right) = 0\) là:
\(x = 3\)
\(x = - 2\)
\(x = 3\) và \(x = - 2\)
\(x = 4\)
Có mấy bước để giải phương trình chứa ẩn ở mẫu
\(1\)
\(2\)
\(3\)
\(4\)
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x + 2}} + 1 = \frac{3}{{x - 3}}\) là:
\(x \ne - 2\)
\(x \ne 3\)
\(x \ne - 2\) và \(x \ne 3\)
\(x = - 2\) và \(x = 3\)
Tập nghiệm của phương trình \(\left( {3x + 1} \right)\left( {2 - 3x} \right) = 0\) là:
\(S = \left\{ {\frac{{ - 1}}{3};\frac{2}{3}} \right\}\)
\(S = \left\{ {\frac{{ - 1}}{2}} \right\}\)
\(S = \left\{ {\frac{{ - 1}}{3};\frac{{ - 2}}{3}} \right\}\)
\(S = \left\{ {\frac{1}{2};\frac{3}{2}} \right\}\)
Phương trình \(\frac{2}{{x - 2}} - \frac{3}{{x - 3}} = \frac{{3x - 20}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\) có nghiệm là:
\(x = 5\)
\(x = 6\)
\(x = 8\)
\(x = 10\)
\(x = - 2\) là nghiệm của phương trình nào sau đây:
\({x^2} + 7x = 0\)
\({\left( {3x + 2} \right)^2} - 4{x^2} = 0\)
\(2x\left( {x + 6} \right) + 5\left( {x + 6} \right) = 0\)
\(x\left( {3x + 5} \right) - 6x - 10 = 0\)
Điều kiện xác định của phương trình \(\frac{1}{{x - 1}} - \frac{{4x}}{{{x^3} - 1}} = \frac{x}{{{x^2} + x + 1}}\)
\(x \ne 0\)\(\)
\(x \ne 0\) và \(x \ne 0\)
\(x \ne 1\)
\(x \ne 1\)và\(x \ne 2\)
Tập nghiệm của phương trình \(x\left( {3x + 5} \right) - 6x - 10 = 0\) là:
\(S = \left\{ {\frac{{ - 5}}{3};2} \right\}\)
\(S = \left\{ {\frac{5}{3};2} \right\}\)
\(S = \left\{ {\frac{5}{3}; - 2} \right\}\)
\(S = \left\{ {\frac{{ - 5}}{3}; - 2} \right\}\)
Trong một khu đất có dạng hình vuông, người ta dành một mảnh đất, có dạng hình chữ nhật ở góc khu đất để làm bể bơi (hình vẽ). Biết diện tích bể bơi bằng \(1250\)cm2. Tính độ dài cạnh khu đất đó.
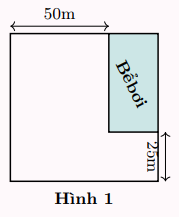
\(72m\)
\(73m\)
\(74m\)
\(75m\)
Cho hai biểu thức \(A = \frac{3}{{3x + 1}} + \frac{2}{{1 - 3x}}\); \(B = \frac{{x - 5}}{{9{x^2} - 1}}\). Với giá trị nào của \(x\) thì hai biểu thức \(A\) và \(B\) có cùng một giá trị?
0
1
5
7
Cho phương trình \(\frac{1}{{x + 1}} - \frac{{2{x^2} - m}}{{{x^3} + 1}} = \frac{4}{{{x^2} - x + 1}}\). Biết \(x = 0\) là một nghiệm của phương trình. Tìm các nghiệm còn lại.
\(x = - 5\)
\(x = 5\)
\(x = 2\)
\(x = - 1\)
Nghiệm của phương trình\(\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{x + 2}} = \frac{{16}}{{{x^2} - 4}}\) là:
\(x = - 2\)
\(x = 2\)
Vô nghiệm
\(x = - 2\) và \(x = 2\)
Độ cao \(h\) (mét) của một quả bóng gôn sau khi được đánh \(t\) giây được cho bởi công thức \(h = t\left( {20 - 5t} \right)\). Có thể tính được thời gian bay của quả bóng từ khi được đánh đến khi chạm đất không?
10 giây
12 giây
20 giây
25 giây
Trong một khu vườn hình vuông có cạnh bằng \(15\)m người ta làm một lối đi xunh quanh có bề rộng là \(x\) (m). Để diện tích phần đất còn lại là \(169\)m2 thì bề rộng \(x\) của lối đi là bao nhiêu?
\(0,5m\)
\(1m\)
\(1,5m\)
\(2m\)
Một doanh nghiệp sử dụng than để sản xuất. Doanh nghiệp đó lập kế hoạch tài chính cho viẹc loại bỏ chất ô nhiễm trong khí thải theo dự kiến sau: Để loại bỏ \(p\% \) chất ô nhiễm trong khí thải thì chi phí \(C\) (triệu đồng) được tính theo công thức \(C = \frac{{80}}{{100 - p}}\), với \(0 \le p < 100\). Với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được bao nhiêu phầm trăm chất gây ô nhiễm trong khí thải (làm tròn kết quả đến hàng phần mười).
\(90\% \)
\(99\% \)
\(99,8\% \)
\(98,9\% \).
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích để làm sân vườn như hình vẽ. Biết diện tích đất làm nhà là 100m2. Hỏi \(x\) bằng bao nhiêu mét?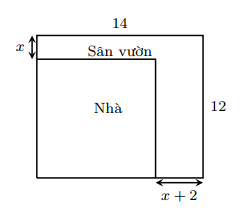
\(1,5m\)
\(1,75m\)
\(2m\)
\(2,2m\).
Phương trình \({x^3} + 8 = {x^2} - 4\) có bao nhiêu nghiệm?
1 nghiệm
2 nghiệm
3 nghiệm
Vô nghiệm.
Biết nồng độ muối của nước biển là \(3,5\% \) và khối lượng riêng của nước biển là \(1020\)g/ml. Từ 2 lít nước biển như thế, người ta hòa tan thêm muối để được dung dịch có nồng độ muối là \(20\% \). Tính khối lượng muối cần thêm.
420,7 (g)
420,75 (g)
420 (g)
420,5 (g).
Tìm \[m\] để phương trình \[(2m - 5)x - 2{m^2} + 8 = 43\] có nghiệm \(x = - 7\).
\[m = 0\] hoặc \[m = 7\].
\[m = 1\] hoặc \[m = - 7\].
\[m = 0\] hoặc \[m = - 7\].
\[m = - 7\].
Số nghiệm của phương trình: \[({x^2} + 9)\left( {x--1} \right) = ({x^2} + 9)\left( {x + 3} \right)\] là
\[2\].
\[1\].
\[0\].
\[3\].
Cho hai biểu thức: \(A = 1 + \frac{1}{{2 + x}}\) và \(B = \frac{{12}}{{{x^3} + 8}}\). Tìm \(x\) sao cho \(A = B\).
\[x = 0\]
\[x = 1\]
\[x = - 1\]
\[x = 0\]; \[x = 1\]
Cho phương trình\[\left( 1 \right)\]: \(\frac{1}{x} + \frac{2}{{x - 2}} = 0\) và phương trình\[\left( 2 \right)\]: \(\frac{{x - 1}}{{x + 2}} - \frac{x}{{x - 2}} = \frac{{5x - 2}}{{4 - {x^2}}}\). Khẳng định nào sau đây là đúng.
Hai phương trình có cùng điều kiện xác định.
Hai phương trình có cùng số nghiệm.
Phương trình \[\left( 2 \right)\] có nhiều nghiệm hơn phương trình \[\left( 1 \right)\]
Phương trình \[\left( 2 \right)\] có ít nghiệm hơn phương trình \[\left( 1 \right)\]








