238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P3)

Họ các nguyên hàm của hàm số $f\left(x\right)=x{\ln }^{2}x$  là

Cho hàm số f(x) liên tục trên đoạn [0;1] thỏa mãn 2f(x)+3f(1-x)=x$\sqrt{1-x}$   với mọi x$\in [0;1]$. Tích phân  ${\int }_0^{2}xf\text{'}\left(\frac{x}{2}\right)dx$ bằng

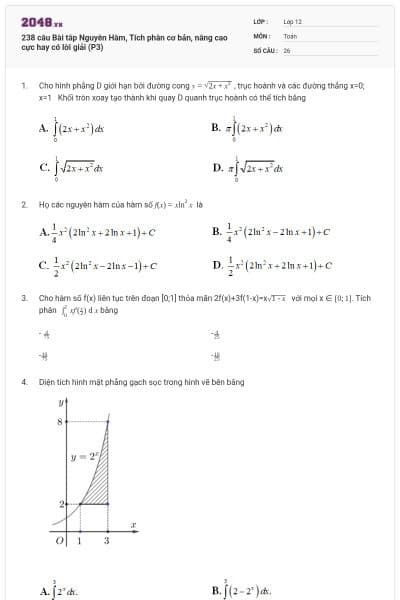
Diện tích hình mặt phẳng gạch sọc trong hình vẽ bên bằng

Cho hàm số  f(x) thỏa mãn f(x)f'(x)=1 với mọi

x$\in$R. Biết ${\int }_1^{2}f\left(x\right)dx=a$ và f(1)=b, f(2)=c Tích phân  ${\int }_1^2\frac{x}{f\left(x\right)}dx$ bằng

Gọi (H) là hình phẳng giới hạn bởi parabol

y=${(x-3)}^2$ trục hoành và trục tung. Gọi k1,k2(k1>k2) lần lượt là hệ số góc của đường thẳng qua điểm A(0;9 và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k1-k2 bằng

Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tích phân ${\int }_{-3}^{5}f\left(x\right)dx$  bằng

Cho ${\int }_0^1\frac{x^2+x+1}{x+1}dx=a+b\ln 2$ với a,b là các số hữu tỷ . Giá trị của a+b bằng

Cho ${\int }_0^{1}x\ln (2+x^2)dx=a\ln 3+b\ln 2+c$ với a,b,c là các số hữu tỷ. Giá trị của a+b+c bằng

Nguyên hàm của hàm số ^{$f\left(x\right)=\frac{x^2}{{(x2-1)}^2}̣̣$} là

Cho ${\int }_1^e(x+2)\ln xdx=a{e}^2+b$  với a, b là các số hữu tỉ. Giá trị biểu thức a + b bằng

Cho hàm số   có đồ thị như hình vẽ bên. Tích phân  ${\int }_{-2}^{3}f\left(x\right)dx$ bằng

Tích phân $\int x\ln (x+3)dx=a+b\ln 2+c\ln 5$ với a,b,c  là các số hữu tỷ. Giá trị của abc bằng

Biết  ${\int }_{\frac{\mathrm{\pi }}{4}}^{\frac{\mathrm{\pi }}{3}}\frac{1}{{\cos }^{4}x+\sin x\mathrm{co}{s}^{3}x}dx=a-\sqrt{b}+c\ln 2+d\ln (1+\sqrt{3)}$  với a,b,c,d là các số hữu tỉ. Giá trị của abcd bằng

Cho hàm số y=f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3]  thoả mãn f(0)=3, f(3)=8 và${\int }_0^3\frac{(f\text{'}{\left(x\right))}^2}{f\left(x\right)+1}dx=\frac{4}{3}$  Giá trị của f(2) bằng

 Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn $xf\left(x\right).f\text{'}\left(x\right)=f^2\left(x\right)-x,\forall x\in \mathrm{ℝ}$và f(2)=1 .Tích phân  bằng

Cho hình phẳng giới hạn bởi các đường $y=\sqrt{\tan x};y=0;x=0;x=\frac{\mathrm{\pi }}{4}$ quay xung quanh trục Ox. Tính thể tích vật thể tròn xoay được sinh ra.

Cho hai hàm số

y$=x^3+a{x}^2+bx+c(a,b,c\in R)$có đồ thị (C) và 

y=$=m{x}^2+nx+p(m,n,p\in \mathrm{ℝ})$có đồ thị (P)  như hình vẽ. Diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?

Tính thể tích V của vật thể giới hạn bởi hai  mặt phẳng x=0 và x=4 , biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x(0<x<4) thì được thiết diện là nửa hình tròn bán kính $R=x\sqrt{4-x}$

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{3}{x}^3-x^2-\frac{1}{3}x+1$ và trục hoành như hình vẽ bên. Mệnh đề nào sau đây sai?

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=4-$\frac{1}{x^2}$(x>0) đường thẳng y=-1,đường thẳng y=1 và trục tung được diện tích như sau:  

Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:    

Cho ${\int }_1^{2}f\left(x\right)dx=1$ và ${\int }_1^{4}f\left(t\right)dt=-3$. Giá trị của ${\int }_2^{4}f\left(u\right)du$ là:    

Cho F(x)=${\int }_1^x(t^2+1)dt$. Giá trị nhỏ nhất của F(x) trên đoạn [-1;1]  là: 

Diện tích hình phẳng giới hạn bởi đồ thị các hàm số

y=$-x^2+2x+1,y=2x^2-4x+1$ là :

Cho ${\int }_1^{2}f\left(x\right)dx=2$. Khi đó ${\int }_1^4\frac{f(\sqrt{x)}}{\sqrt{x}}dx$ bằng