25 câu hỏi
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
6
4
2
8
Cho số phức z thỏa mãn |z+2i+3| = |-i|. Tìm giá trị nhỏ nhất của |z|.
3105
35
105
310
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
-x + 7y + 9 = 0
x + 7y - 9 = 0
x + 7y + 9 = 0
x - 7y + 9 = 0
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
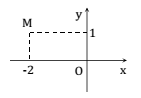
z4= 2 + i
z2= 1 + 2i
z3= -2 + i
z1= 1 - 2i
Tìm tổng các giá trị của m để hai phương trình + mz + 2 = 0 và - + 2z + m có ít nhất một nghiệm phức chung.
-2
3
1
5
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5. Tìm phần ảo của số phức w =
21009
0
-21009
2019
Cho số phức z thỏa mãn: |z-3-2i| = 1. Tìm giá trị nhỏ nhất của |-1-i|
4
- 1
6
+ 1
Cho số phức z thỏa mãn: |z|= 4. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (3+4i)z + i là một đường tròn có bán kính là:
4.
5.
20.
22.
Tính môđun của số phức z biết = (4-3i)(1+i).
|z| = 25
|z| = 7
|z| = 5
|z| =
Kết quả của phép tính: P = 1 + i + ..... +
P = 0
P = 1
P = 1 + i
P = 2i
Mệnh đề nào sau đây đúng.
z.z¯¯ ≠z¯.z¯
z'z = z.z'|z|2
z.z¯ = 2a
z + z¯ = 2a
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
Đường thẳng.
Đường tròn.
Một điểm xác định.
Elip.
Gọi z1, z2, z3 và z4 là bốn nghiệm phức của phương trình - 12 = 0. Tính tổng T = |z1| + |z2| + |z3| + |z4|
T = 4
T =
T = 4 +
T = 0
Tìm phần thực phần ảo của số phức z thỏa mãn điều kiện sau: (2+3i)z = z - 1
Phần thực a = - phần ảo b =
Phần thực a = phần ảo b = -
Phần thực a = - phần ảo b = i
Phần thực a = phần ảo b =
Cho hai số phức z = (2x+3) + (3y-1)i và z' = (y-1)i. Ta có z = z' khi:
x = 32; y = 0
x = -32; y = 0
x = 3; y = 13
x = 0; y = -32
Tìm tham số m để số phức z = m(-5) - mi là số thuần ảo.
m = 0
m =
m = 0; m =
m = 5
Trong mặt phẳng phức cho điểm . Trong các khẳng định sau, khẳng định nào sai?
Điểm M biểu diễn cho số phức có môđun bằng 3.
Điểm M biểu diễn cho số phức có phần thực bằng 4.
Điểm M biểu diễn cho số phức u = + 4i.
Điểm M biểu diễn cho số phức có phần thực bằng .
Gọi là hai nghiệm phức của phương trình - 2z + 2 = 0. Khi đó giá trị biểu thức A = bằng:
0
0
Cho số phức z thỏa mãn |z+i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:
I(0;-1)
I(0;-3)
I(0;3)
I(0;1)
Tìm |z| biết z = 1 + 2i+
|z| = 0
|z| = 1
|z| = -1
|z| = 2
Phương trình: - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
Trong 2 nghiệm có một nghiệm bằng 0.
Cả 2 nghiệm đều là số thực.
Cả 2 nghiệm đều là số thuần ảo.
Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo.
Cho số phức z thỏa mãn |z + 2 - i| + |z - 5 + 6i| = 7. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z - 1 + 2i|. Tổng M + m là:
2.
3
4
7
Biết các số phức z có tập hợp điểm trên mặt phẳng tọa độ là hình tròn tô đậm như hình vẽ. Modul lớn nhất của số phức z là:
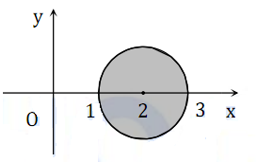
= 1
= 2
= 3
=
Cho số phức z thỏa mãn: |z-3-4i| = 1. Tìm giá trị lớn nhất của |z|
4
5
6
7
Gọi z1, z2 là hai nghiệm của phương trình + z + 1 = 0. Tính giá trị của biểu thức ?
1.
-1

