220 Bài trắc nghiệm Hàm số từ đề thi thử THPTQG 2019 cực hay có lời giải chi tiết (P2)

Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = $\frac{x^2+x+4}{x+1}$ trên đoạn [0;2]. Giá trị của a+A bằng

Tìm giá trị lớn nhất của hàm số f(x) = $x^3-3x^2-9x+10$ trên [-2;2].

Tích giá trị lớn nhất và giái trị nhỏ nhất của hàm số y =  trên đoạn $\left[\frac{1}{2};2\right]$ bằng:

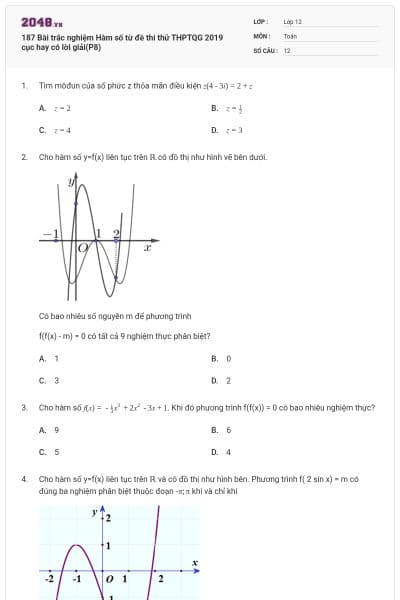
Cho hàm số y = f(x) liên tục trên đoạn [-2;6] và có đồ thị như hình vẽ bên dưới.

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-2;6]. Giá trị của M - m bằng

Bất phương trình $\frac{x-1}{x+1}\ge$m có nghiệm thuộc đoạn [1;2] khi và chỉ khi

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = $\frac{3\sin x+2}{\sin x +\hspace{0.17em}1}$ trên đoạn $\left[0;\frac{\mathrm{\pi }}{2}\right]$. Khi đó giá trị của $M^2+m^2$ là

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = $\sqrt{x-2}+\sqrt{4-x}$ lần lượt là M và m. Chọn câu trả lời đúng.

Tìm giá trị của tham số thực m để giá trị nhỏ nhất của hàm số y = $\frac{2x+m}{x+1}$ trên đoạn [0;4] bằng 3.

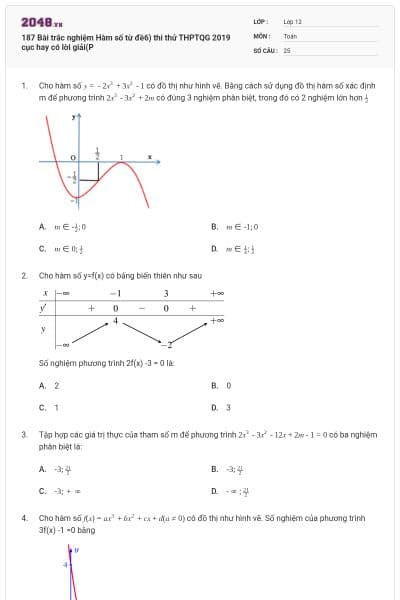
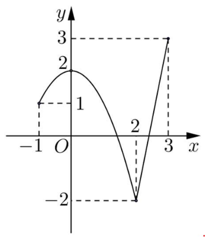
Cho hàm số y = f(x) xác định và liên tục trên R có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số. Giá trị của M – m bằng

Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) = 2x + $\cos \frac{\mathrm{\pi x}}{2}$ trên đoạn [-2;2]. Giá trị của m + M bằng

Giá trị nhỏ nhất của hàm số y = $x{e}^{x+1}$ trên [-2;0] bằng :

Tìm x để hàm số y = x + $\sqrt{4-x^2}$ đạt giá trị lớn nhất

Giá trị lớn nhất M của hàm số y = x + $\frac{4}{x+1}$ trên đoạn [0;4]

Gọi T là giá trị lớn nhất của hàm số y = $x^3-3x^2-9x-1$ trên đoạn [-1;2]. Tính giá trị T.

Giá trị nhỏ nhất m của hàm số y = $x^3 - 7x^2 + 11x -2$ trên đoạn [0;2] là:

Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6)$\sqrt{x^2+4}$ trên đoạn [0;3] có dạng a - b$\sqrt{c}$ với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.

Cho hàm số f(x) = ${\sin }^{3}x$ - 3sinx + 2. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho. Khi đó M + 2m là

Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - $\sqrt{4-x^2}$. Tính tổng M + m.

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = $x^3-3x^2$ trên đoạn [-1;1]. Tính M + m.

Tìm giá trị nhỏ nhất của hàm số y = x + $\frac{9}{x}$ trên đoạn [2;4].

Cho hàm số y = f(x) có đạo hàm f'(x) = x(x+1)${\left(x-2\right)}^2$ với mọi x$\in \mathrm{ℝ}$. Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1;2] là

Cho hàm số y = f(x) có đạo hàm f'(x) = $x^4+3x^3-3x^2+3x-4$ với mọi $x\in \mathrm{ℝ}$. Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-4;2] là

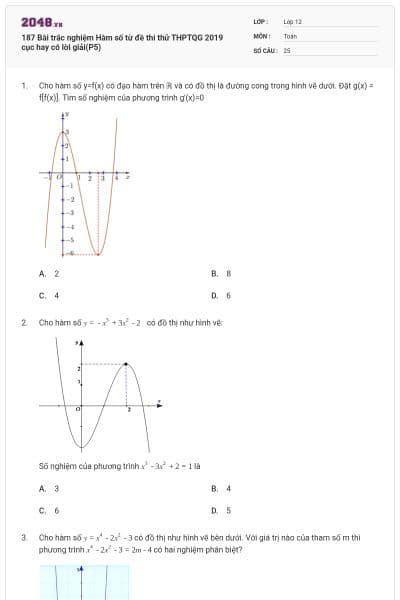
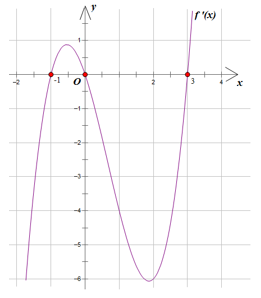
Cho hàm số y = f(x) có đồ thị của đạo hàm f'(x) như hình vẽ bên dưới. Giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;3] là

Cho hàm số f(x) có đạo hàm f'(x) = -x${\left(x-2\right)}^2\left(x-3\right), \forall x\in \mathrm{ℝ}$. Giá trị lớn nhất của hàm số đã cho trên đoạn [0;4] bằng

Giá trị lớn nhất của hàm số y = 4$x^2 +\hspace{0.17em}\frac{1}{x} - 2$ trên đoạn [-1;2] bằng

Giá trị lớn nhất của hàm số y = $x^3 - 3x^2$ trên đoạn [-1;1] là:

Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = $\frac{1}{2}x-\sqrt{x+1}$ trên đoạn [0;3]. Tính tổng S = 2m + 3M

Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y = x + $\sqrt{4-x^2}$. Khi đó

Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = $\frac{2\cos x +\hspace{0.17em}1}{\cos x - 2}$. Khi đó ta có