22 câu trắc nghiệm Toán 12 Kết nối tri thức Bài tập cuối chương IV (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hai tích phân \(\int\limits_{ - 2}^5 {f\left( x \right)dx} = 8\) và \(\int\limits_{ - 2}^5 {g\left( x \right)dx} = 3\). Tính \(I = \int\limits_{ - 2}^5 {\left( {f\left( x \right) - g\left( x \right)} \right)dx} \).
\(I = 77\).
\(I = 5\).
\(I = - 11\).
\(I = 11\).
Cho hàm số \(f\left( x \right)\) có một nguyên hàm trên ℝ là \(F\left( x \right)\). Biết \(F\left( 0 \right) = 1\) và \(F\left( 2 \right) = 7\), giá trị của \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
6.
4.
2.
−4.
\(\int {3{x^2}dx} \) bằng
\(\frac{1}{3}{x^3} + C\).
2x + C.
3x3 + C.
x3 + C.
Hàm số \(F\left( x \right) = {x^2} + x\) là một nguyên hàm của hàm số nào sau đây?
\(f\left( x \right) = \frac{1}{3}{x^3}\).
\(f\left( x \right) = \frac{1}{3}{x^3} + C\).
\(f\left( x \right) = 2x + 1\).
\(f\left( x \right) = 2x\).
Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x = 0;x = \pi \), đồ thị hàm số \(y = \cos x\) và trục \(Ox\) là
\(S = - \int\limits_0^\pi {\cos xdx} \).
\(S = \int\limits_0^\pi {\cos xdx} \).
\(S = \int\limits_0^\pi {\left| {\cos x} \right|dx} \).
\(S = \pi \int\limits_0^\pi {{{\cos }^2}xdx} \).
Tích phân \(\int\limits_1^e {\frac{1}{x}dx} \) bằng
1.
2.
0.
e.
Tích phân \(I = \int\limits_1^3 {\frac{{2x - 1}}{{x + 1}}dx} = a - b\ln 2\). Khi đó tổng của \(a + b\) là
10.
2.
7.
1.
Biết tích phân \(\int\limits_{\frac{\pi }{4}}^{\frac{{2\pi }}{3}} {\frac{3}{{{{\sin }^2}x}}dx} = a + b\sqrt 3 \left( {a,b \in \mathbb{Z}} \right)\). Tính \({a^2} + {b^2}\).
10.
4.
\(\frac{9}{2}\).
2.
Công thức nào sau đây mô tả diện tích của phần gạch chéo trong hình vẽ bên dưới?
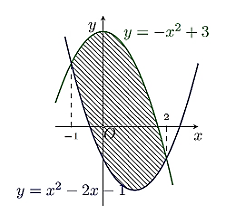
\(S = \int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \).
\(S = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
\(S = \int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \).
\(S = \pi \int\limits_{ - 1}^2 {\left( {2{x^2} + 2x - 4} \right)dx} \).
Tìm một nguyên hàm F(x) của hàm số \(f\left( x \right) = 2x - {e^x}\), biết \(F\left( 0 \right) = - 2\).
\(F\left( x \right) = x - {e^x} + 1\).
\(F\left( x \right) = {x^2} - {e^x} - 1\).
\(F\left( x \right) = {x^2} - {e^x} - 2\).
\(F\left( x \right) = {x^2} - {e^x} + 1\).
Gọi V là thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 1, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 1) thì được thiết diện là một hình tam giác đều có cạnh là \(x\sqrt {8 - {x^2}} \). Giá trị của V bằng
\(\frac{{37\sqrt 3 }}{{15}}\).
\(\frac{{37\sqrt 3 }}{{60}}\).
\(\frac{{37\sqrt 3 }}{{30}}\).
\(\frac{{39\sqrt 3 }}{{60}}\).
Cho hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {9x + 7} \), trục hoành và các đường thẳng x = 2, x = 7. Thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox là
\(312\pi \).
\(\frac{{475\pi }}{2}\).
\(\frac{{531\pi }}{2}\).
\(\frac{{475}}{2}\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho \(\int\limits_{ - 3}^0 {f\left( x \right)dx} = - 2024\) và \(\int\limits_{ - 3}^0 {g\left( x \right)dx} = - 2025\).
a) \(\int\limits_0^{ - 3} {f\left( x \right)dx} = 2024\).
b) \(\int\limits_{ - 3}^0 { - 3g\left( x \right)dx} = - 6075\).
c) \(\int\limits_{ - 3}^0 {\left[ {f\left( x \right) - g\left( x \right) + 1} \right]dx} = 4\).
d) Cho \(m,n\) là các hằng số. Nếu \(\int\limits_{ - 3}^0 {\left[ {mf\left( x \right) - ng\left( x \right)} \right]dx} = 2026\) và \(\int\limits_{ - 3}^0 {\left[ { - nf\left( x \right) + mg\left( x \right)} \right]dx} = 2023\) thì \(m + n = - 3\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ {a;b} \right]\), biết \(F\left( x \right) = {x^4} - 2{x^2} + 1\) là một nguyên hàm của hàm số \(g\left( x \right) = f'\left( x \right) - 4x\). Với \(a,b,C\) là các hằng số.
a) \(f'\left( x \right) = 4{x^3}\).
b) \(\int {g\left( x \right)dx} = F\left( x \right) + C\).
c) \(\int\limits_a^b {g\left( x \right)dx} = F\left( a \right) - F\left( b \right)\).
d) Hàm số \(y = f\left( x \right)\) có đúng một điểm cực trị.
Cho hàm số \(f\left( x \right)\) xác định trên ℝ\{0} thỏa mãn \(f\left( x \right) = x + 5 - \frac{6}{x}\).
a) f(x) là một nguyên hàm của hàm số \(g\left( x \right) = 1 + \frac{6}{{{x^2}}}\).
b) \(\int {f\left( x \right)dx} = \frac{1}{2}{x^2} + 5x - 6\ln x + C\).
c) Gọi F(x) là một nguyên hàm của hàm số f(x) và thỏa mãn F(1) = 5. Khi đó \(F\left( 2 \right) = 5 + \int\limits_1^2 {f\left( x \right)dx} \).
d) Gọi G(x) là một nguyên hàm của hàm số f(x) thỏa mãn G(1) = 4 và G(2) + G(−1) = 5. Khi đó \(G\left( { - 6} \right) = - 13 - 6\ln 3\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) và \(f'\left( x \right)\) liên tục trên khoảng \(\left( {0; + \infty } \right)\) có bảng biến thiên như sau:
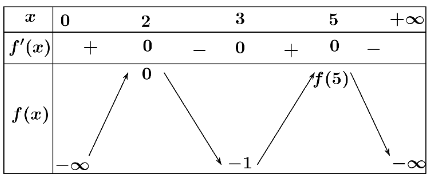
a) \(\int\limits_2^5 {f'\left( x \right)dx} = f\left( 5 \right) - f\left( 2 \right)\).
b)\(\int\limits_2^3 {f'\left( x \right)dx} = 1\).
c) Diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right):y = f'\left( x \right),y = 0,x = 2,x = 3\) bằng \(\frac{1}{2}\).
d) Biết rằng \(\int\limits_2^5 {\left| {f'\left( x \right)} \right|dx} = 5\), suy ra \(f\left( 5 \right) = 5\).
Cho đồ thị các hàm số \(y = f\left( x \right) = x + 1\) và \(y = g\left( x \right) = 0,{7^x}\) như hình vẽ
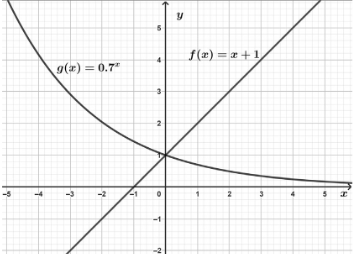
a) \(\int\limits_{ - 1}^0 {f\left( x \right)dx} = \frac{1}{2}\).
b) Thể tích vật thể tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 1,x = 0\) xung quanh trục hoành bằng 9π.
c) Thể tích vật thể tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường \(y = g\left( x \right)\), trục hoành và hai đường thẳng \(x = 0,x = 2\) quanh trục hoành có giá trị xấp xỉ bằng 7,9 (làm tròn kết quả đến hàng phần mười).
d) Khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = g\left( x \right)\), trục hoành và hai đường thẳng \(x = - 1;x = 2\) quanh trục hoành có thể tích xấp xỉ bằng 4,4 (làm tròn kết quả đến hàng phần mười).
PHẦN III. TRẢ LỜI NGẮN
Một vật chuyển động chậm dần với vận tốc \(v\left( t \right) = 160 - 10t\) (m/s). Tính quãng đường mà vật di chuyển trong khoảng thời gian từ thời điểm \(t = 0\) đến thời điểm mà vật dừng lại.
Cho hàm số \(f\left( x \right) = \frac{a}{{{x^2}}} + \frac{b}{x} + 2\) với a, b là các số hữu tỉ thỏa điều kiện \(\int\limits_{\frac{1}{2}}^1 {f\left( x \right)dx} = 2 - 3\ln 2\). Tính \(T = a + b\).
Cho \(F\left( x \right) = \left( {a{x^2} + bx + c} \right){e^x}\) là một nguyên hàm của hàm số \(f\left( x \right) = \left( {{x^2} + 1} \right){e^x}\). Tính tổng \(S = a + b + c\)
Ông A dự định xây “tường cong” trong sân trượt patin là một khối bê tông có chiều cao từ mặt đất lên là 3,5 m. Giao của mặt tường cong và mặt đất là đoạn thẳng AB = 4m. Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với AB tại A là một hình tam giác vuông cong ACE với AC = 4m, CE = 3,5m và cạnh cong AE nằm trên một đường parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí M là trung điểm của AC thì đường cong có độ cao 1m (xem hình). Tính thể tích bê tông cần sử dụng để tạo nên khối tường cong đó.
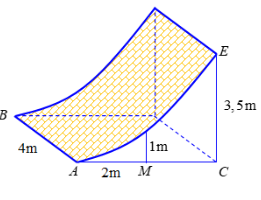
Một mảnh đất có hình dạng là hình thang cong có các thông số như hình vẽ, biết phần đường cong là phần đồ thị của hàm số \(y = a\sqrt x \). Diện tích của mảnh đất đó là bao nhiêu? (làm tròn đến hàng phần chục).