22 câu trắc nghiệm Toán 12 Cánh diều Bài tập cuối chương IV (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Diện tích hình phẳng giới hạn bởi hai parabol \(y = - {x^2} + 3;y = 2{x^2} + 3x - 3\)và hai đường thẳng \(x = - 2;x = 1\) bằng:
\(11,5.\)
\(12,5.\)
\(10,5.\)
\(13,5.\)
Hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = \frac{1}{x}\) trên \(\left( { - \infty ;0} \right)\) thỏa mãn \(F\left( { - 2} \right) = 0\).Khẳng định nào sau đây đúng?
\(F\left( x \right) = \ln \left| x \right| + \ln 2,\forall x \in \left( { - \infty ;0} \right)\).
\(F\left( x \right) = \ln \left( {\frac{{ - x}}{2}} \right),\forall x \in \left( { - \infty ;0} \right)\).
\(F\left( x \right) = \ln \left| x \right| + C,\forall x \in \left( { - \infty ;0} \right)\) với C là một số thực bất kì.
\(F\left( x \right) = \ln \left( { - x} \right) + C,\forall x \in \left( { - \infty ;0} \right)\) với C là một số thực bất kì.
Cho hàm số \(f(x)\) có đạo hàm \(f'(x)\)liên tục trên \(\mathbb{R}\),\(\int\limits_0^4 {f'\left( x \right)dx = 6} \)và \(f(0) = 2\). Giá trị của \(f(4)\)là:
4.
8.
7.
\(2.\)
Cho hàm số \(f(x)\)liên tục trên \(\mathbb{R}\)và \(\int\limits_1^2 {f(x)dx = 4} \). Tính \(\int\limits_1^2 {3f(x)dx} \).
4.
8.
12.
\(6.\)
Một ô tô đang chạy với vận tốc 30 m/s thì người lái xe đạp phanh. Từ thời điểm đó ô tô chuyển động với vận tốc \(v(t) = 30 - 3t\) (m/s), trong đó t (tính bằng giây) là thời gian kể từ lúc bắt đầu đạp phanh. Quãng đường ô tô di chuyển từ lúc đạp phanh đến khi dừng hẳn bằng bao nhiêu mét?
170 (m).
150 (m)
100 (m).
140 (m).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = cosx\), trục hoành và hai đường thẳng \(x = \frac{\pi }{6};x = \frac{\pi }{4}\)bằng:
\(\frac{{\sqrt 2 - 1}}{2}.\)
\(\sqrt 2 - 1.\)
\(\sqrt 2 + 1.\)
\(\frac{{1 - \sqrt 2 }}{2}.\)
Thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi đồ thị hàm số \(y = x + 1\), trục hoành và hai đường thẳng \(x = - 1;x = 2\) bằng:
\(V = \frac{{9\pi }}{2}.\)
\(V = \frac{{15\pi }}{2}.\)
\(V = 21\pi .\)
\(V = 9\pi .\)
Biết \(\int {f(x)dx = \frac{{{3^x}}}{{\ln 3}}} + C\)(C là hằng số). Khẳng định nào sau đây đúng?
\(f(x) = {3^x}.\)
\(f(x) = \frac{{{3^x}}}{{\ln 3}} + C.\)
\(f(x) = \frac{{{3^x}}}{{\ln 3}}.\)
\(f(x) = {3^x} + C.\)
Cho hai hàm số \(f(x),g(x)\) liên tục trên K. Khẳng định nào sau đây là đúng?
\(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx.} } \)
\(\int {kf(x)dx = k\int {f(x)dx} } \) \((k \ne 0).\)
\(\int {\left[ {f(x).g(x)} \right]dx = \int {f(x)dx.\int {g(x)dx.} } } \)
\(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx.} } \)
Biết \[\int\limits_0^1 {\left( {{x^2} + 3{x^3}} \right)dx} = \frac{m}{n}\left( {m,n \in \mathbb{Z}} \right)\]. Khẳng định nào sau đây đúng?
\(12m - 13n = 0.\)
\(12n - 13m = 0.\)
\(12m + 13n = 0.\)
\(12n + 13m = 0.\)
Cho một vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ \(x = - 1\)và \(x = 1.\)Một mặt phẳng vuông góc với trục Ox tại \(x( - 1 \le x \le 1)\)cắt vật thể đó theo một mặt cắt là hình vuông có cạnh bằng \(3x.\)Thể tích V của vật thể đó bằng:
\(V = \int\limits_{ - 1}^1 {3x} dx.\)
\(V = \int\limits_{ - 1}^1 {{{(3x)}^2}} dx.\)
\(V = \int\limits_{ - 1}^1 {(6x} {)^2}dx.\)
\(V = \int\limits_{ - 1}^1 {6x} dx.\)
Cho hàm số \(f(x)\) xác định trên một khoảng K, C là hằng số. Hàm số\(F(x)\)là một nguyên hàm của hàm số \[f(x)\]trên \[K\] nếu:
\(F'(x) = f(x),\forall x \in K.\)
\(f'(x) = - F(x) + C,\forall x \in K.\)
\(f'(x) = F(x),\forall x \in K.\)
\(F'(x) = - f(x) + C,\forall x \in K.\)
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \(\mathbb{R}\) và \(\int\limits_1^3 {f(x)dx = } 10\).
a) \(F'(x) = f(x),\forall x \in \mathbb{R}.\)
b) \(F(3) + F(1) = 10\).
c) \(\int\limits_{}^{} {f(x)} dx = F(x) + C\), với C là một hằng số.
d) \(\int\limits_1^3 {(x + f(x))} dx = 14.\)
Cho \(({H_1})\) là hình phẳng giới hạn bởi đồ thị của hàm số \(f(x) = {x^2}\), trục \(Ox\)và đường thẳng \(x = - 1\); \(({H_2})\) là hình phẳng giới hạn bởi đồ thị của hai hàm số \(f(x) = {x^2}\) và \(g(x) = - x\).
a) Đồ thị của hai hàm số \(f(x)\)và \(g(x)\)cắt nhau tại hai điểm có hoành độ lần lượt là \(0\)và \( - 1\).
b) Diện tích hình phẳng \(({H_1})\) bằng \(\frac{\pi }{3}.\)
c) Thể tích khối tròn xoay sinh ra khi quay hình \(({H_1})\) quanh trục \(Ox\) bằng \(\frac{\pi }{5}.\)
d) Diện tích của \(({H_1})\) gấp đôi diện tích của \(({H_2})\).
Cho hàm số \(f\left( x \right) = {x^2} + 2x\) và \(F\left( x \right)\) là một nguyên hàm của hàm số\(f\left( x \right)\).
a)\[\int\limits_1^3 {f\left( x \right)dx} = F\left( 3 \right) - F\left( 1 \right)\].
b) Nếu \(F\left( 0 \right) = 1\) thì \(F\left( 2 \right) = \frac{{25}}{3}\).
c) Nếu \[\int\limits_0^2 {kf\left( x \right)dx} = 2\] thì \(k = \frac{3}{{10}}\).
d) Biết \[\int\limits_1^3 {\frac{{f\left( x \right)}}{{{x^2}}}dx} = a + a\ln b\], \(a,b \in \mathbb{Z}\). Khi đó: \(3a - 5b = - 8\).
Cho hàm số \(f\left( x \right)\) xác định trên ℝ\{0} thỏa mãn \(f\left( x \right) = x + 5 - \frac{6}{x}\).
a) f(x) là một nguyên hàm của hàm số \(g\left( x \right) = 1 + \frac{6}{{{x^2}}}\).
b) \(\int {f\left( x \right)dx} = \frac{1}{2}{x^2} + 5x - 6\ln x + C\).
c) Gọi F(x) là một nguyên hàm của hàm số f(x) và thỏa mãn F(1) = 5. Khi đó \(F\left( 2 \right) = 5 + \int\limits_1^2 {f\left( x \right)dx} \).
d) Gọi G(x) là một nguyên hàm của hàm số f(x) thỏa mãn G(1) = 4 và G(2) + G(−1) = 5. Khi đó \(G\left( { - 6} \right) = - 13 - 6\ln 3\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - x\;\;khi\;x \le 0\\x\;\;\;\;\;\;\;\;\;khi\;x > 0\end{array} \right.\).
a)\(\int\limits_2^5 {f\left( x \right)dx} = \int\limits_2^5 {xdx} \).
b)\(\int\limits_{ - 4}^{ - 2} {f\left( x \right)dx} = 6\).
c) \(I = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_{ - 1}^3 {f\left( x \right)dx} = \frac{{20}}{3}\).
d) \(\int\limits_{ - 2}^1 {f\left( x \right)dx} = \frac{{31}}{6}\).
PHẦN III. TRẢ LỜI NGẮN
Cho hàm số \(y = f(x)\) liên tục trên đoạn \([0;4]\) có đồ thị trên đoạn \([0;4]\) gồm một phần của đường parabol \(\left( P \right)\) và một phần của đường thẳng \(\left( d \right)\) như hình vẽ sau. Tính tích phân . (làm tròn kết quả đến hàng phần mười)
![Cho hàm số \(y = f(x)\) liên tục trên đoạn \([0;4]\) có đồ thị trên (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/13-1760667750.png)
Bác Bình muốn làm một cái cửa bằng inox hình parabol có chiều cao từ mặt đất đến đỉnh là 3 mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Biết rằng giá vật liệu và tiền công mỗi mét vuông là 1700000 đồng. Vậy bác Bình phải trả bao nhiêu tiền để làm cái cửa đó (đơn vị triệu đồng)? ( Làm tròn kết quả đến hàng phần mười)
Một học sinh đang điều khiển xe đạp điện chuyển động thẳng đều với vận tốc \(a\;\left( {{\rm{m/s}}} \right)\). Khi phát hiện có chướng ngại vật phía trước học sinh đó thực hiện phanh xe. Sau khi phanh, xe chuyển động chậm dần đều với vận tốc \(v(t) = a - 2t\left( {{\rm{m/s}}} \right)\), thời gian tính bằng giây. Tìm giá trị lớn nhất của \(a\)để quãng đường xe đạp điện đi được sau khi phanh không vượt quá \(9\;m\).
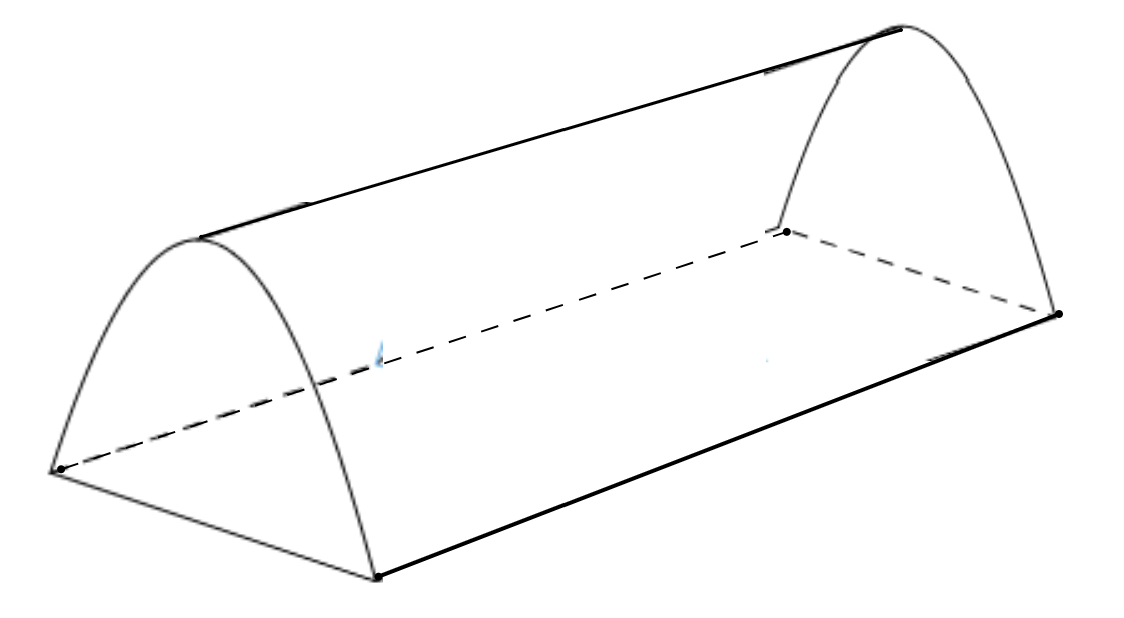
Nhân dịp đi dã ngoại, lớp 12A dự kiến dựng một cái trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 5 mét, đỉnh trại cách nền 3 mét. Thể tích phần không gian bên trong lều trại bằng bao nhiêu mét khối?
Cho hàm số \(f\left( x \right) = \frac{a}{{{x^2}}} + \frac{b}{x} + 2\) với a, b là các số hữu tỉ thỏa điều kiện \(\int\limits_{\frac{1}{2}}^1 {f\left( x \right)dx} = 2 - 3\ln 2\). Tính \(T = a + b\).
