22 câu trắc nghiệm Toán 12 Cánh diều Bài 1. Tính đơn điệu của hàm số (Đúng sai - Trả lời ngắn) có đáp án
37 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số f(x) có bảng biến thiên như sau
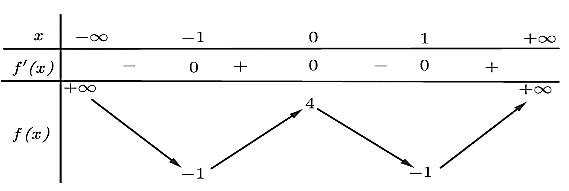
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; −1).
(0; 1).
(−1; 1).
(−1; 0).
Cho hàm số y = f(x) có bảng biến thiên như sau
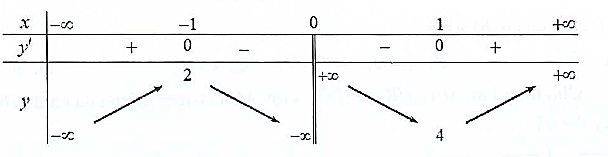
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−1; 1).
(4; +∞).
(−∞; 2).
(0; 1).
Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau
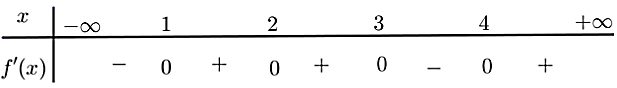
Hàm số nghịch biến trên khoảng nào dưới đây?
(−∞; 1).
(2; 4).
(1; 3).
(3; +∞).
Cho hàm số f(x) xác định trên ℝ và có bảng xét dấu đạo hàm f'(x) như sau:
Khẳng định nào sau đây đúng?
f(−1) > f(3).
f(6) > f(8).
f(−3) > f(−1).
f(5) < f(6).
Cho hàm số y = f(x) có đồ thị như hình.
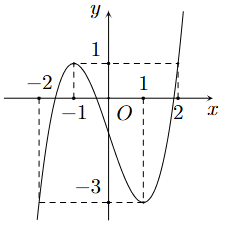
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
(0; 2).
(1; +∞).
(−∞; 1).
(−2; 1).
Cho hàm số 
. Mệnh đề nào dưới đây là đúng?
Hàm số nghịch biến trên ℝ.
Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).
Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
Hàm số đồng biến trên ℝ\{2}.
Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ.
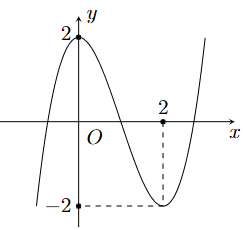
Hàm số y = f(x) đạt cực tiểu tại điểm nào dưới đây?
x = 2.
x = 0.
x = −2.
x = 4.
Cho hàm số y = f(x) có bảng biến thiên như sau
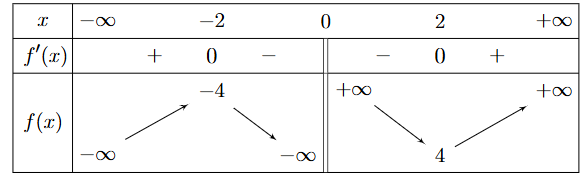
Khẳng định nào sau đây sai?
Hàm số có hai điểm cực trị.
Tọa độ điểm cực đại của đồ thị hàm số là (−2; −4).
Hàm số nghịch biến trên khoảng (−2; 2).
Hàm số đồng biến trên khoảng (3; +∞).
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ, a ≠ 0) có đồ thị là đường cong như hình
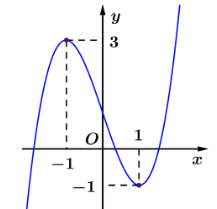
Giá trị cực đại của hàm số đã cho bằng
1.
0.
−1.
3.
Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x + 2)(x2 – 1), ∀x Î ℝ. Số điểm cực trị của hàm số đã cho là
1.
0.
2.
3.
Điểm cực tiểu của hàm số 
là
x = −3.
x = −6.
x = 2.
x = 1.
Cho hàm số y = x3 – 3x + 2. Hàm số đã cho có bao nhiêu cực trị?
2.
0.
1.
3.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
a) Hàm số có hai điểm cực trị
b) Điểm cực đại của đồ thị hàm số là (−2; 2).
c) Điểm cực tiểu của hàm số là −4.
d) Giá trị cực tiểu của hàm số là −15.
a) Hàm số nghịch biến trên khoảng (1; 3).
b) Hàm số đạt cực đại tại x = 3.
c) Hàm số có giá trị cực tiểu là 
.
d) Hàm số có giá trị cực đại là 3.
a) Hàm số nghịch biến trên khoảng (0; 2)
b) Hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
c)Hàm số đạt cực tiểu tại x = −5.
d) Hàm số g(x) = f(3 – 2x) đồng biến trên khoảng (0; 3).
a) Hàm số f(x) có 3 điểm cực trị.
b) Hàm số f(x) đồng biến trên khoảng (−∞; −1).
c) Hàm số f(x) đạt cực đại tại x = 0.
d) f(0) < f(1).
a) Phương trình f'(x) = 0 có hai nghiệm là x = 2 và x = −2.
b) Hàm số y = f(x) đạt cực đại tại x = 2.
c) Hàm số y = f(x) có giá trị cực tiểu bằng f(2).
d) Hàm số y = f(x2) có 3 điểm cực trị.
PHẦN II. TRẢ LỜI NGẮN
Sau khi làm sạch, người ta bơm nước vào một bể bơi. Biết rằng thể tích V(lít) của lượng nước trong bể bơi sau t (phút) bơm được cho bởi công thức 
với 0 ≤ t ≤ 20.
Khi nước được bơm vào bể, tốc độ bơm nước tại thời điểm t được xác định bởi công thức V'(t) với 0 £ t £ 20. Hỏi tốc độ bơm nước tăng trong bao nhiêu phút kể từ khi bắt đầu bơm nước vào bể bơi.
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ
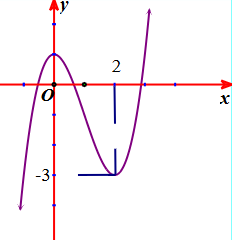
Gọi A(a; b) là điểm cực tiểu của đồ thị hàm số đã cho. Tính giá trị biểu thức P = 2a – b.
Một chất điểm chuyển động theo phương trình 
trong đó t tính bằng giây, s tính bằng mét. Trong 40 giây đầu tiên, chất điểm đó có vận tốc tức thời giảm trong khoảng thời gian (a; b). Tính giá trị biểu thức P = a + 9b.
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 4)(x2 – 2x), ∀x Î ℝ. Biết hàm số y = f(x) nghịch biến trên khoảng (a; b). Tính b – a.
Biết đồ thị hàm số y = x3 – 3x2 + 2ax + b (a; b Î ℝ) có điểm cực tiểu A(2; −2). Tính a + b.
