22 câu trắc nghiệm Toán 11 Kết nối tri thức Bài tập cuối chương 7 có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Một khối lăng trụ có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích của khối lăng trụ đó bằng
15.
90.
10.
30.
Cho một khối chóp có chiều cao bằng h và diện tích đáy bằng B. Nếu giữ nguyên chiều cao h, còn diện tích đáy tăng lên 3 lần thì ta được một khối chóp mới có thể tích là:
V = B.h.
\(V = \frac{1}{6}Bh\).
\(V = \frac{1}{2}Bh\).
\(V = \frac{1}{3}Bh\).
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BA' và CD bằng
45°.
60°.
30°.
90°.
Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a ^ (P). Trong các mệnh đề dưới đây, mệnh đề nào sai?
Nếu b // a thì b ^ (P).
Nếu b Ì (P) thì b ^ a.
Nếu b // (P) thì b ^ a.
Nếu b // a thì b // (P).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD là
\(a\sqrt 3 \).
\(a\sqrt 2 \).
2a.
a.
Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?
Nếu a và b cùng vuông góc với c thì a // b.
Nếu a // b và c ^ a thì c ^ b.
Nếu góc giữa a và c bằng góc giữa b và c thì a // b.
Nếu a và b cùng nằm trong (α), (α) // c thì góc giữa a và c bằng góc giữa b và c.
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
AB ^ (ABC).
AC ^ BD.
CD ^ (ABD).
BC ^ AD.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi M, N lần lượt là trung điểm của BC và AC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng
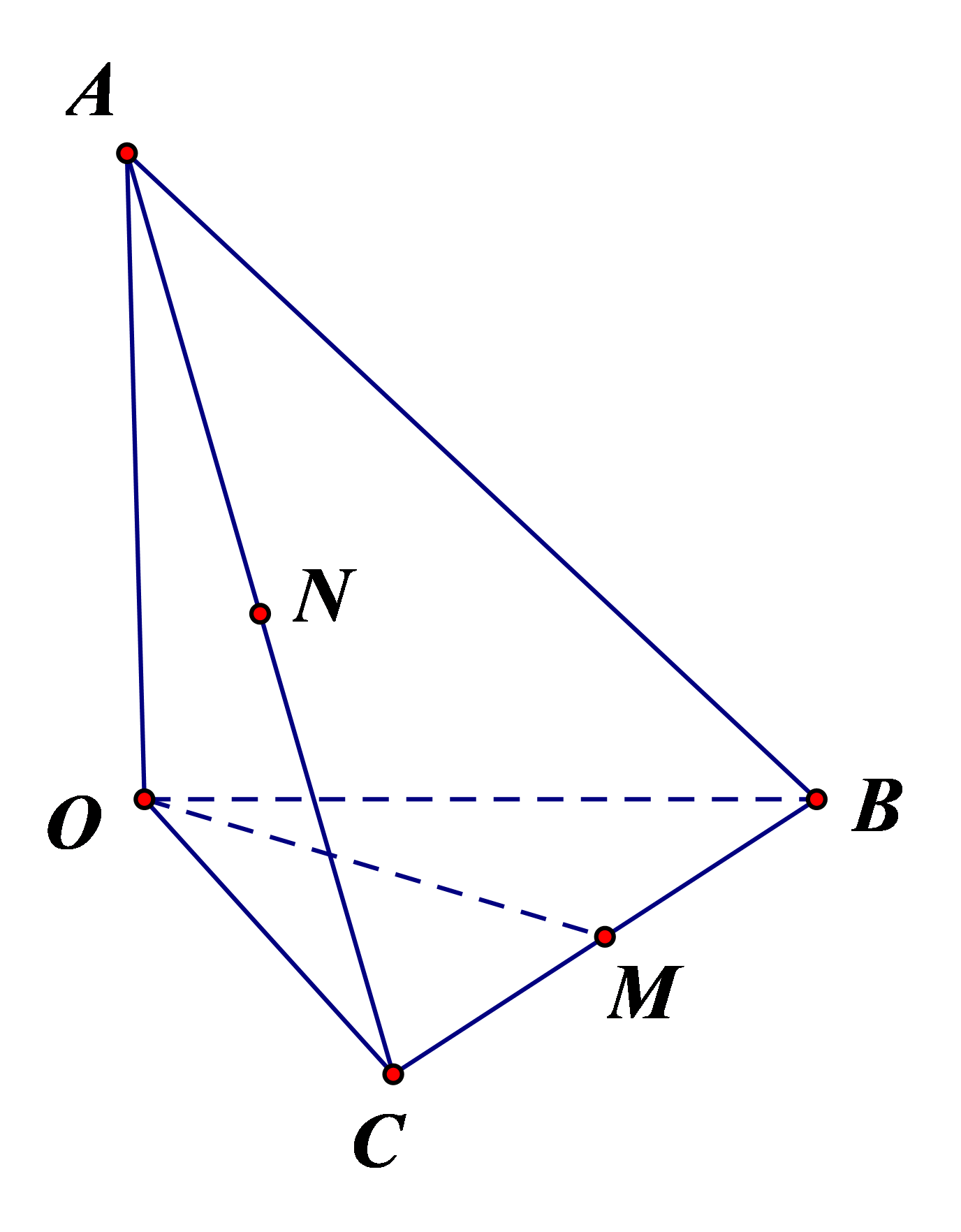
\(\widehat {ABO}\).
\(\widehat {MNO}\).
\(\widehat {NOM}\).
\(\widehat {OMN}\).
Cho hình chóp S.ABC có SA ^ (ABC) và đáy ABC là tam giác đều. Khẳng định nào sau đây sai?
(SAB) ^ (ABC).
Gọi H là trung điểm của cạnh BC. Khi đó \(\widehat {AHS}\) là góc giữa hai mặt phẳng (SBC) và (ABC).
Góc giữa hai mặt phẳng (SBC) và (SAC) là \(\widehat {ACB}\).
(SAC) ^ (ABC).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA ^ (ABCD). Biết rằng \(SA = \frac{{a\sqrt 6 }}{3}\). Tính góc giữa SC và (ABCD).
30°.
60°.
75°.
45°.
Cho hình chóp S.ABC có đáy ABC là tam giác đều, gọi M là trung điểm BC. Biết cạnh bên SA vuông góc với đáy. Góc phẳng nhị diện [S, BC, A] là góc nào dưới đây?
\(\widehat {SBA}\).
\(\widehat {SCA}\).
\(\widehat {SMA}\).
\(\widehat {SAM}\).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt phẳng (SAC) ^ (ABCD). Trong các mệnh đề sau, hãy cho biết mệnh đề nào đúng?
\(\left( {SAC} \right) \bot \left( {SBD} \right)\).
\(\left( {SBD} \right) \bot \left( {ABCD} \right)\).
\[\left( {BCD} \right) \bot \left( {ACD} \right)\].
\(\left( {SAB} \right) \bot \left( {SAD} \right)\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABC có SA ^ (ABC) và SA = \(a\sqrt 5 \), đáy là tam giác vuông tại A với AB = a; AC = 2a. Dựng AK vuông góc với BC và AH vuông góc với SK.
a) Hai đường thẳng BC và AH vuông góc với nhau.
b) Đường thẳng AH vuông góc với mặt phẳng (SBC).
c) Đoạn thẳng AK có độ dài bằng \(\frac{{a\sqrt 5 }}{5}\).
d) Tan góc giữa đường thẳng SA và mặt phẳng (SBC) bằng \(\frac{2}{5}\).
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = BC = a. Cạnh bên SA vuông góc với mặt phẳng đáy (ABC) và SA = a. Gọi I là trung điểm của AC và kẻ IH ^ SC.
a) Đường thẳng SC vuông góc với mặt phẳng (BHI).
b) Độ dài đoạn thẳng BH bằng \(\frac{{a\sqrt 2 }}{2}\).
c) Cosin góc tạo bởi hai đường thẳng IH và BH bằng \(\frac{{\sqrt 3 }}{2}\).
d) Góc giữa hai mặt phẳng (SAC) và (SBC) bằng 60°.
Một người thiết kế một bể kính hình lăng trụ lục giác đều, có cạnh đáy bằng 20 cm, chiều cao bằng 50 cm. Người đó dùng một vòi bơm nước vào bể với tốc độ 200 cm3/s (biết 1 lít nước bằng 1000 cm3), giả sử độ dày kính và đường nối các mép kính là không đáng kể. Khi đó:
a) Bể kính là lăng trụ đứng có đáy là lục giác đều.
b) Diện tích đáy của bể kính là \(40\sqrt 3 \) cm2.
c) Bể chứa được tối đa 52 lít nước (kết quả làm tròn đến hàng đơn vị).
d) Sau khi bơm 2 phút, mực nước trong bể cao 24 cm (kết quả làm tròn đến hàng đơn vị).
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khi đó:
a) Khoảng cách từ A' đến (ABC) bằng a.
b) Khoảng cách từ điểm B đến đường thẳng AC bằng BC.
c) Khoảng cách giữa hai đường thẳng AA' và BC bằng \(\frac{{a\sqrt 3 }}{2}\).
d) Khoảng cách từ điểm A đến (A'BC) bằng \(\frac{{a\sqrt {21} }}{3}\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh AC = a, các cạnh bên \(SA = SB = SC = \frac{{a\sqrt 6 }}{2}\). Gọi H là trung điểm của BC. Khi đó:
a) Đường thẳng SH là chiều cao của khối chóp S.ABC.
b) Thể tích khối chóp S.ABC bằng \(\frac{{{a^3}}}{2}\).
c) Số đo của góc nhị diện [S, AB, C] lớn hơn 65°.
d) Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng \(\frac{{2a}}{{\sqrt 5 }}\).
PHẦN II. TRẢ LỜI NGẮN
Cho khối chóp S.ABCD có đáy là hình vuông cạnh 3, SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng \(\frac{{3\sqrt 2 }}{2}\). Tính thể tích của khối chóp.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. Tính khoảng cách giữa hai đường thẳng AB' và CD'.
Cho hình lăng trụ tam giác ABC.A'B'C' có các cạnh bên hợp với đáy là những góc bằng 60°, đáy ABC là tam giác đều cạnh 1 và A' cách đều A, B, C. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Cho mô hình tạo khung cho rạp xiếc lưu động hình chóp cụt ABCD.A'B'C'D' có hai đáy là hình vuộng cạnh đáy lớn gấp đôi đáy nhỏ. Biết thể tích khối chóp cụt trên là 5600 m3 và chiều cao bằng 6 m. Tính cạnh của đáy lớn.
Cho hình chóp S.ABCD có SA vuông góc với đáy ABCD. Biết đáy ABCD là hình chữ nhật. Biết AB = a, BC = 3a, SB = 2a. Góc giữa SA và mặt phẳng (SBC) là x°. Tính x2 + 100.
