12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Một khối lăng trụ có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích của khối lăng trụ đó bằng
15.
90.
10.
30.
Cho một khối chóp có chiều cao bằng h và diện tích đáy bằng B. Nếu giữ nguyên chiều cao h, còn diện tích đáy tăng lên 3 lần thì ta được một khối chóp mới có thể tích là:
V = B.h.
\(V = \frac{1}{6}Bh\).
\(V = \frac{1}{2}Bh\).
\(V = \frac{1}{3}Bh\).
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BA' và CD bằng
45°.
60°.
30°.
90°.
Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a ^ (P). Trong các mệnh đề dưới đây, mệnh đề nào sai?
Nếu b // a thì b ^ (P).
Nếu b Ì (P) thì b ^ a.
Nếu b // (P) thì b ^ a.
Nếu b // a thì b // (P).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD là
\(a\sqrt 3 \).
\(a\sqrt 2 \).
2a.
a.
Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?
Nếu a và b cùng vuông góc với c thì a // b.
Nếu a // b và c ^ a thì c ^ b.
Nếu góc giữa a và c bằng góc giữa b và c thì a // b.
Nếu a và b cùng nằm trong (α), (α) // c thì góc giữa a và c bằng góc giữa b và c.
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
AB ^ (ABC).
AC ^ BD.
CD ^ (ABD).
BC ^ AD.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi M, N lần lượt là trung điểm của BC và AC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng
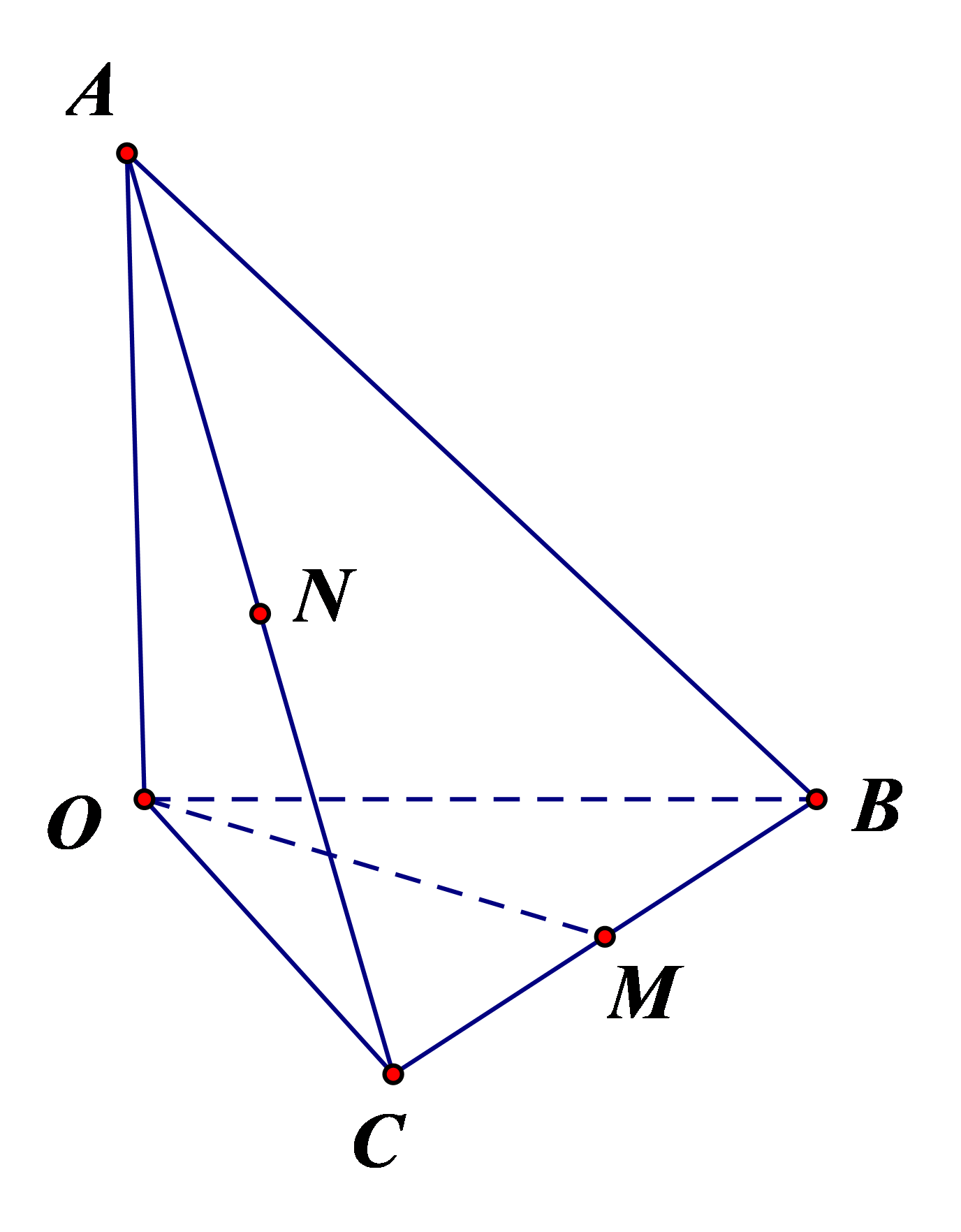
\(\widehat {ABO}\).
\(\widehat {MNO}\).
\(\widehat {NOM}\).
\(\widehat {OMN}\).
Cho hình chóp S.ABC có SA ^ (ABC) và đáy ABC là tam giác đều. Khẳng định nào sau đây sai?
(SAB) ^ (ABC).
Gọi H là trung điểm của cạnh BC. Khi đó \(\widehat {AHS}\) là góc giữa hai mặt phẳng (SBC) và (ABC).
Góc giữa hai mặt phẳng (SBC) và (SAC) là \(\widehat {ACB}\).
(SAC) ^ (ABC).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA ^ (ABCD). Biết rằng \(SA = \frac{{a\sqrt 6 }}{3}\). Tính góc giữa SC và (ABCD).
30°.
60°.
75°.
45°.
Cho hình chóp S.ABC có đáy ABC là tam giác đều, gọi M là trung điểm BC. Biết cạnh bên SA vuông góc với đáy. Góc phẳng nhị diện [S, BC, A] là góc nào dưới đây?
\(\widehat {SBA}\).
\(\widehat {SCA}\).
\(\widehat {SMA}\).
\(\widehat {SAM}\).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt phẳng (SAC) ^ (ABCD). Trong các mệnh đề sau, hãy cho biết mệnh đề nào đúng?
\(\left( {SAC} \right) \bot \left( {SBD} \right)\).
\(\left( {SBD} \right) \bot \left( {ABCD} \right)\).
\[\left( {BCD} \right) \bot \left( {ACD} \right)\].
\(\left( {SAB} \right) \bot \left( {SAD} \right)\).
