22 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài tập ôn tập chương 1 (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Chọn góc lượng giác (OM, ON) có số đo bằng \(\frac{\pi }{7}\). Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OM, ON)?
\(\frac{{6\pi }}{7}\).
\(\frac{{ - 11\pi }}{7}\).
\(\frac{{9\pi }}{7}\).
\(\frac{{29\pi }}{7}\).
Biết \(\sin a = - \frac{1}{2}\). Giá trị của sin(π – a) là
\(\sin \left( {\pi - a} \right) = \frac{1}{2}\).
\(\sin \left( {\pi - a} \right) = - \frac{1}{2}\).
\(\sin \left( {\pi - a} \right) = - \frac{{\sqrt 3 }}{2}\).
\(\sin \left( {\pi - a} \right) = \frac{{\sqrt 3 }}{2}\).
Rút gọn biểu thức \(T = \sin \left( {\frac{\pi }{3} + x} \right) - \sin \left( {\frac{\pi }{3} - x} \right)\) ta được kết quả là:
\(T = \frac{{\sqrt 3 }}{2}\).
T = sinx.
\(T = \sqrt 3 \cos x\).
T = sin2x.
Biết tana = 2 và \(0 < a < \frac{\pi }{2}\). Tính cosa.
\(\cos a = \frac{{\sqrt 3 }}{3}\).
\(\cos a = - \frac{{\sqrt 5 }}{5}\).
\(\cos a = \frac{1}{2}\).
\(\cos a = \frac{{\sqrt 5 }}{5}\).
Tập xác định của hàm số \(y = \frac{{1 - \cos x}}{{\sin x}}\) là
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Rút gọn biểu thức \(\sin \left( {a - 19^\circ } \right).\cos \left( {a + 11^\circ } \right) - \sin \left( {a + 11^\circ } \right)\cos \left( {a - 19^\circ } \right)\) ta được
sin2a.
cos2a.
\(\frac{1}{2}\).
\( - \frac{1}{2}\).
Cho đồ thị hàm số y = cosx có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? 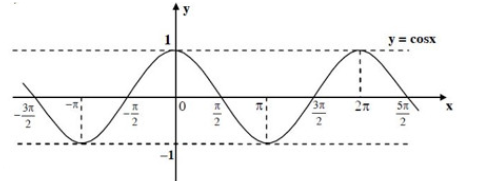
(0; π).
\(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
(π; 2π).
\(\left( { - \frac{{3\pi }}{2}; - \pi } \right)\).
Số đo theo đơn vị rađian của góc 315° là
\(\frac{{2\pi }}{7}\).
\(\frac{{7\pi }}{2}\).
\(\frac{{4\pi }}{7}\).
\(\frac{{7\pi }}{4}\).
Hàm số y = 2coss2024x – 1 có tập giá trị T là
\(T = \left[ { - 3;1} \right]\).
T = [−1; 1].
T = [1; 3].
T = [−2023; 2023].
Nghiệm của phương trình \(\sin \frac{x}{2} = 1\) là
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\).
\(x = \pi + k4\pi ,k \in \mathbb{Z}\).
\(x = k2\pi ,k \in \mathbb{Z}\).
\(x = \pi + k2\pi ,k \in \mathbb{Z}\).
Rút gọn biểu thức \(A = \frac{{\sin a + \sin 3a + \sin 5a}}{{\cos a + \cos 3a + \cos 5a}}\) ta được
A = sin3a.
A = cos3a.
A = 1 – tan3a.
A = tan3a.
Phương trình \(\tan \left( {x + \frac{\pi }{6}} \right) = - 1\) có nghiệm là
\(x = - \frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}\).
\(x = - \frac{{5\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho cosx = −0,3 và \( - 3\pi < x < - \frac{{5\pi }}{2}\).
a) sinx < 0.
b) cotx < 0.
c) \(\tan x = \frac{{91}}{9}\).
d) \({\cot ^2}x = \frac{9}{{91}}\).
Cho đồ thị hàm số y = f(x) như hình vẽ
![Hàm số y = cosx là hàm số chẵn trên đoạn [−3π; 3π]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/11-1749895963.png)
a) Hàm số y = cosx là hàm số chẵn trên đoạn [−3π; 3π].
b) Trên đoạn [−3π; 3π] phương trình \(\cos x = \frac{1}{3}\) có 6 nghiệm phân biệt.
c) \(f\left( {\frac{{3\pi }}{2}} \right) = 1\).
d) Hàm số y = cosx đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Cho \(\sin \alpha = \frac{2}{3}\) với \(\frac{\pi }{2} < \alpha < \pi \).
a) \(1 - 2{\sin ^2}\alpha = - \frac{1}{9}\).
b) \(\cos \alpha = - \frac{{\sqrt 5 }}{3}\).
c) \(\sin 2\alpha = - \frac{{4\sqrt 5 }}{9}\).
d) \(\cos \left( {\alpha + \frac{\pi }{3}} \right) = \frac{{\sqrt 5 - 2\sqrt 3 }}{6}\).
Cho hàm số y = tan2x – 1.
a) Tập xác định của hàm số trên là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
b) Hàm số trên là hàm số chẵn.
c) Tập giá trị của hàm số trên là [0; +∞).
d) Chỉ có duy nhất một giá trị x Î [0; π] sao cho y = 0.
Cho hai hàm số \(f\left( x \right) = \frac{3}{2} + 3\cos x\) và g(x) = sinx + cosx.
a) Hàm số g(x) là hàm số lẻ.
b) Hàm số f(x) đạt giá trị nhỏ nhất khi x = π + k2π (k ∈ ℤ).
c) Giá trị lớn nhất của hàm số f(x) bằng \(\frac{9}{2}\).
d) Có 4 giá trị của x thuộc đoạn [0; 2π] sao cho f(x) = 3g(x).
PHẦN II. TRẢ LỜI NGẮN
Nếu tanα = 2 thì giá trị \(25{\cos ^2}\alpha + \tan \left( {\alpha + \frac{\pi }{4}} \right)\) bằng bao nhiêu?
Nghiệm dương nhỏ nhất của phương trình \(\sin \left( {x + \frac{\pi }{6}} \right) = \sin 2x\) là \(\frac{\pi }{a}\) với a là số nguyên dương. Giá trị của a bằng bao nhiêu?
Mực nước của một dòng sông lên xuống theo thủy chiều trong ngày. Độ sâu h (m) của mực nước trên sông tính theo thời gian t (giờ) trong một ngày (0 £ t < 24) cho bởi công thức \(h = 2\sin \left( {\frac{{\pi t}}{6}} \right) + 11\). Có bao nhiêu thời điểm trong ngày thì độ sâu của mực nước là 12 m.
Giả sử số miligam của các chất ô nhiễm trong một mét khối không khí của một tháng trong ngày thứ t tại thành phố công nghiệp X được cho bởi hàm số \(P\left( t \right) = a + b\sin \frac{{\pi t}}{{10}}\) (a, b > 0, t Î ℤ, 0 < t £ 30). Biết chất ô nhiễm trong một mét khối không khí cao nhất là 50 miligam và thấp nhất là 20 miligam. Hỏi ngày thứ hai thì số miligam của các chất ô nhiễm trong một mét khối không khí tại thành phố công nghiệp X là bao nhiêu? (kết quả làm tròn đến hàng phần mười).
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với t Î ℤ và 0 < t £ 365. Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?
