12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Chọn góc lượng giác (OM, ON) có số đo bằng \(\frac{\pi }{7}\). Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OM, ON)?
\(\frac{{6\pi }}{7}\).
\(\frac{{ - 11\pi }}{7}\).
\(\frac{{9\pi }}{7}\).
\(\frac{{29\pi }}{7}\).
Biết \(\sin a = - \frac{1}{2}\). Giá trị của sin(π – a) là
\(\sin \left( {\pi - a} \right) = \frac{1}{2}\).
\(\sin \left( {\pi - a} \right) = - \frac{1}{2}\).
\(\sin \left( {\pi - a} \right) = - \frac{{\sqrt 3 }}{2}\).
\(\sin \left( {\pi - a} \right) = \frac{{\sqrt 3 }}{2}\).
Rút gọn biểu thức \(T = \sin \left( {\frac{\pi }{3} + x} \right) - \sin \left( {\frac{\pi }{3} - x} \right)\) ta được kết quả là:
\(T = \frac{{\sqrt 3 }}{2}\).
T = sinx.
\(T = \sqrt 3 \cos x\).
T = sin2x.
Biết tana = 2 và \(0 < a < \frac{\pi }{2}\). Tính cosa.
\(\cos a = \frac{{\sqrt 3 }}{3}\).
\(\cos a = - \frac{{\sqrt 5 }}{5}\).
\(\cos a = \frac{1}{2}\).
\(\cos a = \frac{{\sqrt 5 }}{5}\).
Tập xác định của hàm số \(y = \frac{{1 - \cos x}}{{\sin x}}\) là
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Rút gọn biểu thức \(\sin \left( {a - 19^\circ } \right).\cos \left( {a + 11^\circ } \right) - \sin \left( {a + 11^\circ } \right)\cos \left( {a - 19^\circ } \right)\) ta được
sin2a.
cos2a.
\(\frac{1}{2}\).
\( - \frac{1}{2}\).
Cho đồ thị hàm số y = cosx có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
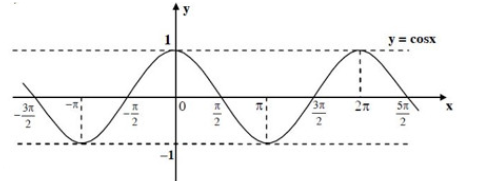
(0; π).
\(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
(π; 2π).
\(\left( { - \frac{{3\pi }}{2}; - \pi } \right)\).
Số đo theo đơn vị rađian của góc 315° là
\(\frac{{2\pi }}{7}\).
\(\frac{{7\pi }}{2}\).
\(\frac{{4\pi }}{7}\).
\(\frac{{7\pi }}{4}\).
Hàm số y = 2coss2024x – 1 có tập giá trị T là
\(T = \left[ { - 3;1} \right]\).
T = [−1; 1].
T = [1; 3].
T = [−2023; 2023].
Nghiệm của phương trình \(\sin \frac{x}{2} = 1\) là
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\).
\(x = \pi + k4\pi ,k \in \mathbb{Z}\).
\(x = k2\pi ,k \in \mathbb{Z}\).
\(x = \pi + k2\pi ,k \in \mathbb{Z}\).
Rút gọn biểu thức \(A = \frac{{\sin a + \sin 3a + \sin 5a}}{{\cos a + \cos 3a + \cos 5a}}\) ta được
A = sin3a.
A = cos3a.
A = 1 – tan3a.
A = tan3a.
Phương trình \(\tan \left( {x + \frac{\pi }{6}} \right) = - 1\) có nghiệm là
\(x = - \frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}\).
\(x = - \frac{{5\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{{5\pi }}{{12}} + k\pi ,k \in \mathbb{Z}\).
\(x = - \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}\).
