12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho x, y > 0 và α, βÎ ℝ. Đẳng thức nào sau đây là sai?
xα + yα = (x + y)α.
(xy)α = xα.yα.
(xα)β = xαβ.
xαxβ = xα + β.
Cho biểu thức \(P = {x^{ - \frac{3}{4}}}\sqrt {\sqrt {{x^5}} } ,x > 0\). Khẳng định nào sau đây là đúng?
\(P = {x^{\frac{1}{2}}}\).
\(P = {x^{ - 2}}\).
\(P = {x^{\frac{1}{2}}}\).
\(P = {x^2}\).
Biết \({a^{\frac{7}{4}}} < {a^{\frac{8}{5}}}\) và \({\log _b}\frac{{\sqrt 3 }}{2} > {\log _b}\frac{{\sqrt 5 }}{3}\). Chọn khẳng định đúng
0 < a < 1 < b.
0 < a < b < 1.
0 < b < 1 < a.
1 < a < b.
Hàm số \(y = \frac{1}{{{5^x} - 1}}\) có tập xác định là
ℝ\{0}.
(0; +∞).
(−∞; 0).
ℝ.
Cho 0 < a ≠ 1, b > 0 thỏa \({\log _a}b = \sqrt 3 \). Tính \(S = {\log _{\sqrt a }}\sqrt[3]{b}\).
\(\frac{{2\sqrt 3 }}{5}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{{2\sqrt 3 }}{3}\).
Tập nghiệm S của bất phương trình là \({\log _{\frac{1}{2}}}x < - 4\) là
S = (16; +∞).
\(\left( { - \infty ;\frac{1}{{16}}} \right)\).
\(\left( {\frac{1}{{16}}; + \infty } \right)\).
(−∞; 16).
Cho bất phương trình 5x < 125. Số nghiệm dương của bất phương trình là
4.
1.
3.
2.
Đồ thị hàm số như hình vẽ là đồ thị của hàm số nào sau đây
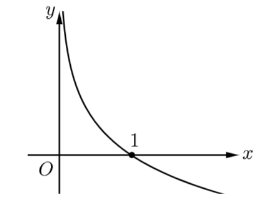
\(y = {\left( {\frac{2}{9}} \right)^x}\).
\(y = {\log _{\frac{2}{9}}}x\).
y = 3x.
\(y = {\left( {\frac{9}{2}} \right)^x}\).
Tập nghiệm của bất phương trình 22x < 2x + 6 là
(0; 6).
(−∞; 6).
(0; 64).
(6; +∞).
Tập nghiệm S của bất phương trình log3(2x – 1) < 2 là
S = (−∞; 5).
\(S = \left( {\frac{1}{2};5} \right)\).
S = (5; +∞).
\(S = \left[ {\frac{1}{2};5} \right)\).
Giá trị của \(K = {\left( {\frac{1}{{81}}} \right)^{ - 0,75}} + {\left( {\frac{1}{{27}}} \right)^{ - \frac{4}{3}}}\) bằng
K = 18.
K = 108.
K = 180.
K = 54.
Cho loga3 = 5. Tính P = loga(3a5).
P = 25.
P = 12.
P =10.
P = 125.
