22 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài tập cuối chương 3 (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hai dãy (un) và (vn) thỏa mãn \(\lim {u_n} = \sqrt 3 \) và limvn = 2. Giá trị của \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng
\(2\sqrt 3 \).
\(\frac{{\sqrt 3 }}{2}\).
\(2 + \sqrt 3 \).
\( - 2 + \sqrt 3 \).
Tính giới hạn \(I = \lim \left( {\sqrt {{n^2} + 2n + 3} - n} \right)\).
1.
0.
2.
3.
Tính \(\lim \left( {3 + 2n + {n^3}} \right)\).
−∞.
+∞.
1.
−1.
Số thập phân vô hạn tuần hoàn 0,17232323… được biểu diễn bởi phân số?
\(\frac{{1706}}{{9900}}\).
\(\frac{{153}}{{990}}\).
\(\frac{{164}}{{990}}\).
\(\frac{{853}}{{4950}}\).
Cho \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - 2\). Giá trị \(\mathop {\lim }\limits_{x \to 3} \left[ {f\left( x \right) + 4x - 1} \right]\) bằng
5.
6.
−11.
9.
Tính \(\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} - 16}}{{x - 4}}\).
7.
8.
5.
6.
Tính giới hạn \(I = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{2x + 1}}\).
−2.
\( - \frac{3}{2}\).
2.
\(\frac{3}{2}\).
Cho \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt {x - 2} + 3\;\;khi\;x \ge 2\\ax - 1\;\;\;\;\;\;\;\;\;khi\;x < 2\end{array} \right.\) và \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) tồn tại. Tính a.
1.
\( - 2\).
3.
2.
Tính giới hạn \(\mathop {\lim }\limits_{x \to - {3^ - }} \frac{{2{x^2} + 5x - 3}}{{{{\left( {x + 3} \right)}^2}}}\).
−∞.
2.
−2.
+∞.
Cho f(x) và g(x) là hai hàm số liên tục trên khoảng (a; b). Tìm mệnh đề sai trong các mệnh đề sau?
Hàm số h(x) = f(x) – g(x) liên tục trên khoảng (a; b).
Hàm số k(x) = f(x)g(x) liên tục trên khoảng (a; b).
Hàm số \(u\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục trên khoảng (a; b).
Hàm số v(x) = mf(x) + ng(x) liên tục trên khoảng (a; b) với m, n là các hằng số.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 2}}\;\;khi\;x \ne 2\\a\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;x = 2\end{array} \right.\). Hàm số liên tục tại x = 2 khi a bằng
1.
0.
2.
−1.
Hàm số nào dưới đây gián đoạn tại điểm x0 = 1?
\(y = \frac{{x - 1}}{{{x^2} + 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \sqrt {x + 1} \).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Biết giới hạn \(\mathop {\lim }\limits_{n \to + \infty } \frac{{ - 3{n^3} + 1}}{{2n + 5}} = a\) và \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{{( - 1)}^n} \cdot {5^n}}}{{{2^n} + {5^{2n}}}} = b\). Khi đó:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( { - 3{n^2} + \frac{1}{n}} \right) = a\).
b) \(x = b\) là hoành độ giao điểm của đường thẳng \(y = 2x\) với trục hoành.
c) \(\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{1}{{2024}}} \right)^n} = b\).
d) Cho cấp số cộng \(\left( {{u_n}} \right)\) với công sai \(d = \frac{1}{2}\) và \({u_1} = b\), thì \({u_3} = 2\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} - 4x + 4} }}{{x - 2}}\;\;khi\;x < 2\\m{x^2} - 3\;\;\;\;khi\;x \ge 2\end{array} \right.\)(m là tham số).
a) Khi m = 1 thì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\).
b) Hàm số f(x) liên tục tại x = 2 khi m = 1.
c) f(2) = 4m – 3.
d) \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 2\;\;\;\;\;\;\;\;\;\;\;khi\;x < - 1\\\sqrt {{x^2} + 1} + m\;\;khi\;x \ge - 1\end{array} \right.\). Khi đó
a) Giới hạn \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \sqrt 5 + m\).
b) Giới hạn \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = - 3\).
c) Giới hạn\(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \sqrt 2 + m\).
d) Khi \(m = 3 + \sqrt 2 \) thì hàm số đã cho có giới hạn tại x0 = −1.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{4 - {x^2}}}{{\sqrt {x + 2} - 2}}\;khi\;x > 2\\mx + 8\;\;\;\;\;\;\;khi\;x \le 2\end{array} \right.\) (m là tham số).
a) Tập xác định của hàm số là D = ℝ.
b) Hàm số liên tục tại x = 7 với mọi m.
c) Hàm số không liên tục tại x = 0 với mọi m.
d) Hàm số f(x) liên tục tại điểm x0 = 2 khi m = −12.
Biết rằng khi nung nóng một vật với nhiệt độ tăng từ 20°C, mỗi phút tăng 4°C trong 70 phút, sau đó giảm mỗi phút 2°C trong 50 phút. Hàm số biểu thị nhiệt độ (°C) theo thời gian t (phút) có dạng \(T\left( t \right) = \left\{ \begin{array}{l}20 + 4t\;\;khi\;0 \le t \le 70\\a - 2t\;\;\;\;khi\;70 < t \le 120\end{array} \right.\) (a là hằng số).
a) Nhiệt độ ban đầu là 20°C.
b) Nhiệt độ lúc 10 phút là 60°C.
c) T(t) là hàm số liên tục trên tập xác định ∀a Î ℝ.
d) Với a = 440°C thì T(t) là hàm số liên tục trên tập xác định.
PHẦN II. TRẢ LỜI NGẮN
Biết các số thực a, b thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + ax + b}}{{x - 1}} = 2025\). Tính 2a +b.
Giới hạn của hàm số \(L = \mathop {\lim }\limits_{x \to 5} \frac{{\sqrt {x + 4} - 3}}{{{x^2} - 25}} = \frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản). Tính a + b.
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}10\;\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;0 \le x \le 5\\{x^2} + ax + 10\;khi\;x > 5\end{array} \right.\). Tìm giá trị của a để hàm số liên tục tại x0 = 5.
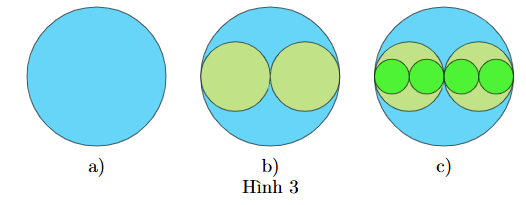
Từ tờ giấy, cắt một hình tròn bán kính R cm như hình 3a. Tiếp theo, cắt hai hình tròn bán kính \(\frac{R}{2}\) rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính \(\frac{R}{4}\) rồi chồng lên các hình trước như hình 3c. Cứ tiếp tục mãi. Khi đó tổng diện tích của các hình tròn là \(a\pi {R^2}\), aÎ ℤ. Tìm a.
Một quả bóng cao su được thả từ độ cao 81 m. Mỗi lần chạm đất quả bóng lại nảy lên hai phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa. (đơn vị mét).
