22 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài tập cuối chương 2 (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho dãy số (un): \({u_n} = \frac{n}{{n + 2}},n \in \mathbb{N}*\). Số hạng thứ 13 của dãy số là:
\(\frac{{13}}{{14}}\).
\(\frac{{13}}{{15}}\).
\(\frac{{13}}{{11}}\).
\(\frac{{15}}{{13}}\).
Cho dãy số (un) biết \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = {u_n} + n\end{array} \right.\)với ∀n Î ℕ*. Giá trị u1 + u2 + u3 bằng
18.
13.
12.
16.
Trong các dãy số sau, dãy số nào là một cấp số cộng.
1; −3; −6; −9; −12; ….
1; −2; −4; −6; −8; ….
1; −3; −7; −11; −15; ….
1; −3; −5; −7; −9; ….
Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng.
un = 7 – 3n.
un = 7 – 3n.
\({u_n} = \frac{7}{{3n}}\).
un = 7.3n.
Cho cấp số cộng (un) có số hạng đầu u1 = −5 và công sai d = 3. Mệnh đề nào sau đây đúng?
u10 = 35.
u13 = 31.
u15 = 34.
u15 = 45.
Cho cấp số cộng (un) có u1 = 4 và d = −5. Tổng 100 số hạng đầu tiên của cấp số cộng bằng
−24350.
24350.
−24600.
24600.
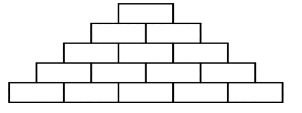
Một người muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức tường gạch với xi măng (mô hình như hình vẽ bên), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên gạch?
12550.
125250.
25250.
250500.
Một cấp số nhân có hai số hạng liên tiếp là 3 và 12. Số hạng tiếp theo của câp số nhân là
15.
21.
36.
48.
Tìm b > 0 để các số \(\frac{1}{{\sqrt 2 }};\sqrt b ;\sqrt 2 \) theo thứ tự đó lập thành một cấp số nhân.
b = −2.
b = −1.
b = 1.
b = 2.
Cho cấp số nhân (un) với u1 = 2 và q = 2. Tính số hạng thứ 2020.
22020.
22021.
22022.
22019.
Cho cấp số nhân 5; 10; ...; 1280 có bao nhiêu số hạng?
9.
7.
8.
10.
Một khu rừng có trữ lượng gỗ là 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ.
4.105.(0,05)5.
4.105.(1,4)5.
4.105.(1,04)5.
4.(10,4)5.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho dãy số (un) có số hạng tổng quát \({u_n} = \frac{{n + 1}}{{n + 2}}\).
a) \({u_{n + 1}} - {u_n} = \frac{1}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\).
b) un + 1 < un, ∀n ∈ ℕ*.
c) Dãy số (un) là dãy số giảm.
d) Dãy (un) là dãy số bị chặn.
Cho cấp số cộng (un) có số hạng đầu \({u_1} = \frac{3}{2}\), công sai \(d = \frac{1}{2}\).
a) Công thức cho số hạng tổng quát \({u_n} = 1 + \frac{n}{3}\).
b) 5 là số hạng thứ 8 của cấp số cộng đã cho.
c) \(\frac{{15}}{4}\) là một số hạng của cấp số cộng đã cho.
d) Tổng 100 số hạng đầu của cấp số cộng (un) bằng 2620.
Cho cấp số nhân (un) có công bội nguyên và các số hạng thỏa mãn \(\left\{ \begin{array}{l}{u_4} - {u_2} = 54\\{u_5} - {u_3} = 108\end{array} \right.\).
a) Số hạng đầu của cấp số nhân bằng 9.
b) Công bội của cấp số nhân q = 3.
c) Tổng của 9 số hạng đầu tiên bằng 4599.
d) Số 576 là số hạng thứ 6 của cấp số nhân.
Anh An đang tập đầu tư chứng khoán. Ở cuối mỗi lần đầu tư, anh An hoặc mất hết tiền đã đầu tư hoặc lời bằng số tiền đã bỏ ra. Ví dụ nếu anh An đầu tư a đồng, anh An sẽ mất a đồng nếu lỗ và sẽ có a đồng tiền lãi nếu lời.
Lần đầu tiên anh đầu tư 20000 đồng, mỗi lần sau tiền đầu tư gấp đôi lần trước. Anh An lỗ 9 lần liên tiếp và lời ở lần thứ 10.
a) Số tiền đầu tư lần thứ hai là 400000 đồng.
b) Số tiền anh An lỗ lần thứ 9 là 5120000 đồng.
c) Số tiền đã thua trong 5 lần đầu là 620000 đồng.
d) Sau lần thứ 10 thì anh An hòa vốn.
Cho cấp số cộng (un), biết rằng u1 = 5 và tổng của 50 số hạng đầu bằng 5150. Khi đó:
a) Công sai của cấp số cộng bằng 6.
b) Số hạng u85 = 341.
c) Số hạng u10 = 42.
d)Tổng của 85 số hạng đầu S85 = 14705.
PHẦN II. TRẢ LỜI NGẮN
Một hội trường có 10 dãy ghế, mỗi dãy ghế kế tiếp nhiều hơn dãy ghế trước nó 4 ghế. Biết dãy ghế cuối cùng có 45 ghế. Hỏi hội trường có bao nhiêu ghế?
Cho hình vuông cạnh 1024 cm. Chia hình vuông đó thành 4 hình vuông nhỏ bằng nhau, sau đó tô hình vuông nhỏ ở góc trái (tham khảo hình vẽ). Lặp lại thao tác này với hình vuông nhỏ ở góc trên bên phải. Giả sử quá trình trên lặp lại vô hạn lần. Gọi u1; u2; u3; … lần lượt là độ dài cạnh của các hình vuông được tô màu. Tính u8.

Người ta trồng \(3240\) cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng thứ hai trở đi số cây trồng mỗi hàng nhiều hơn \(1\) cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây?
Một em học sinh dùng các que diêm để xếp thành hình tháp có quy luật được thể hiện như trong hình sau:

Hỏi cần bao nhiêu que diêm để xếp thành hình tháp có \(10\) tầng?
Tìm \(x\) để các số \(2;8;x;128\) theo thứ tự đó lập thành một cấp số nhân.
