12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho dãy số (un): \({u_n} = \frac{n}{{n + 2}},n \in \mathbb{N}*\). Số hạng thứ 13 của dãy số là:
\(\frac{{13}}{{14}}\).
\(\frac{{13}}{{15}}\).
\(\frac{{13}}{{11}}\).
\(\frac{{15}}{{13}}\).
Cho dãy số (un) biết \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = {u_n} + n\end{array} \right.\)với ∀n Î ℕ*. Giá trị u1 + u2 + u3 bằng
18.
13.
12.
16.
Trong các dãy số sau, dãy số nào là một cấp số cộng.
1; −3; −6; −9; −12; ….
1; −2; −4; −6; −8; ….
1; −3; −7; −11; −15; ….
1; −3; −5; −7; −9; ….
Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng.
un = 7 – 3n.
un = 7 – 3n.
\({u_n} = \frac{7}{{3n}}\).
un = 7.3n.
Cho cấp số cộng (un) có số hạng đầu u1 = −5 và công sai d = 3. Mệnh đề nào sau đây đúng?
u10 = 35.
u13 = 31.
u15 = 34.
u15 = 45.
Cho cấp số cộng (un) có u1 = 4 và d = −5. Tổng 100 số hạng đầu tiên của cấp số cộng bằng
−24350.
24350.
−24600.
24600.
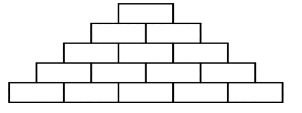
Một người muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức tường gạch với xi măng (mô hình như hình vẽ bên), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên gạch?
12550.
125250.
25250.
250500.
Một cấp số nhân có hai số hạng liên tiếp là 3 và 12. Số hạng tiếp theo của câp số nhân là
15.
21.
36.
48.
Tìm b > 0 để các số \(\frac{1}{{\sqrt 2 }};\sqrt b ;\sqrt 2 \) theo thứ tự đó lập thành một cấp số nhân.
b = −2.
b = −1.
b = 1.
b = 2.
Cho cấp số nhân (un) với u1 = 2 và q = 2. Tính số hạng thứ 2020.
22020.
22021.
22022.
22019.
Cho cấp số nhân 5; 10; ...; 1280 có bao nhiêu số hạng?
9.
7.
8.
10.
Một khu rừng có trữ lượng gỗ là 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ.
4.105.(0,05)5.
4.105.(1,4)5.
4.105.(1,04)5.
4.(10,4)5.
