12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc với đáy ABCD. Xác định khoảng cách từ điểm S đến AB?
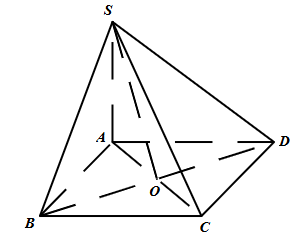
SO.
SA.
SB.
SD.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ^ (ABCD), SA = a. Khoảng cách từ S đến mặt phẳng (ABCD) là
\(a\sqrt 2 \).
a.
\(\frac{a}{2}\).
\(\frac{{3a}}{4}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD). Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
\(\frac{a}{2}\).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{{a\sqrt 2 }}{3}\).
\(\frac{{a\sqrt 2 }}{4}\).
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\], đáy \[ABCD\] là hình thang vuông cạnh \[a\]. Gọi \[I\] và \[J\] lần lượt là trung điểm của \[AB\] và \[CD\]. Tính khoảng cách giữa đường thẳng \[IJ\] và \[\left( {SAD} \right)\].
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{{a\sqrt 3 }}{3}\).
\(\frac{a}{2}\).
\(\frac{a}{3}\).
Cho hình lăng trụ tứ giác đều \[ABCD.A'B'C'D'\]có cạnh đáy bằng\[a\]. Gọi \[M\], \[N\], \[P\] lần lượt là trung điểm của \[AD\], \[DC\], \[A'D'\]. Tính khoảng cách giữa hai mặt phẳng \[\left( {MNP} \right)\] và \[\left( {ACC'} \right)\].
\(\frac{{a\sqrt 3 }}{3}\).
\(\frac{a}{4}\).
\(\frac{a}{3}\).
\(\frac{{a\sqrt 2 }}{4}\).
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh \[a.\] Khoảng cách giữa \[\left( {AB'C} \right){\rm{ v\`a }}\left( {A'DC'} \right)\] bằng :
\(a\sqrt 3 \).
\(a\sqrt 2 \).
\(\frac{a}{3}\).
\(\frac{{a\sqrt 3 }}{3}\).
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\], đáy \[ABCD\] là hình chữ nhật với\[AC = a\sqrt 5 \]và \[BC = a\sqrt 2 \]. Tính khoảng cách giữa \[SD\] và \[BC\].
\(\frac{{3a}}{4}\).
\(\frac{{2a}}{3}\).
\(\frac{{a\sqrt 3 }}{2}\).
\[a\sqrt 3 \].
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a (tham khảo hình vẽ).
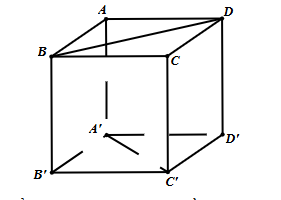
Khoảng cách giữa hai đường thẳng BD và A'C' bằng
a.
\(\sqrt 2 a\).
\(\frac{{\sqrt 3 }}{2}a\).
\(a\sqrt 3 \).
Cho khối chóp có diện tích đáy B = 7 và chiều cao h = 6. Thể tích của khối chóp đã cho bằng
42.
126.
14.
56.
Cho khối lăng trụ có diện tích đáy là 3a2 và chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
a3.
6a3.
3a3.
2a3.
Cho hình lăng trụ đứng ABCD.A'B'C'D', có ABCD là hình vuông cạnh 2a, cạnh \(AC' = 2a\sqrt 3 \). Thể tích khối lăng trụ ABC.A'B'C' bằng
4a3.
3a3.
2a3.
a3.
Tính thể tích của hình chóp cụt đều có đáy lớn là hình vuông, cạnh \(6\;cm\), đáy nhỏ là hình vuông cạnh \(3\;cm\) và chiều cao của hình chóp cụt là \(4\;cm\).
\(84\).
\(32\).
\(12\).
\(96\).
