22 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 3. Hai mặt phẳng vuông góc (Đúng sai - Trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong các mệnh đề sau, mệnh đề nào sau đây là đúng?
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Cho hình chóp S.ABCD có SA ^ (ABCD) và đáy ABCD là hình vuông tâm O. Góc giữa (SBD) và (ABCD) là
\(\widehat {SOA}\).
\(\widehat {SBA}\).
\(\widehat {SDA}\).
\(\widehat {SOC}\).
Cho đường thẳng a không vuông góc với mặt phẳng (α). Có bao nhiêu mặt phẳng chứa a và vuông góc với (α)?
0.
Vô số.
2.
1.
Chohình chóp S.ABCD có đáy ABCD là hình vuông , SA ^ (ABCD). Khẳng định nào sau đây sai?
(SBC) ^ (SAB).
(SAB) ^ (ABCD).
(SAC) ^ (ABCD).
(SAC) ^ (SAD).
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?
(BIH) ^ (SBC).
(SAC) ^ (SAB).
(SBC) ^ (ABC).
(SAC) ^ (SBC).
Trong các khẳng định sau về lăng trụ đều, khẳng định nào sai?
Đáy là đa giác đều.
Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
Các cạnh bên là những đường cao.
Các mặt bên là những hình vuông.
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương.
Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương.
Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
Nếu hình hộp có sáu mặt bằng nhau thì nó là hình lập phương.
Hình chóp tứ giác đều có mặt bên là hình gì?
Tam giác đều.
Tam giác vuông.
Tam giác vuông cân.
Tam giác cân.
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ). Đường thẳng nào sau đây vuông góc với đường thẳng A'C'. 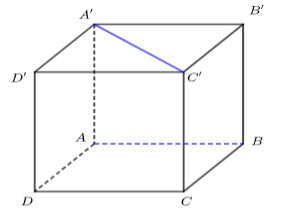
A'D'.
AC.
BD.
CD.
Cho hình lăng trụ đứng ABC.MNP.
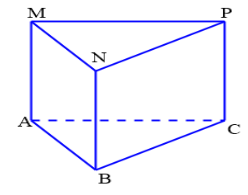
Chọn khẳng định đúng trong các khẳng định sau?
AB ^ (BCPN).
CB ^ (ABNM).
PC ^ (MNP).
BM ^ (MNP).
Cho hình lập phương ABCD.A'B'C'D'. Mặt phẳng (ABCD) không vuông góc với mặt phẳng nào dưới đây? 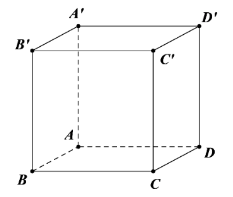
(A'B'C'D').
(ABB'A').
(ADD'A').
(CBB'C').
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ bên dưới).
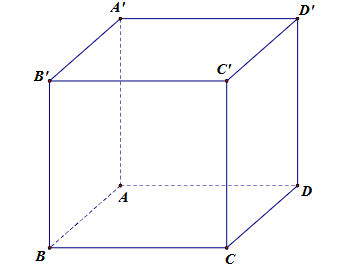
Góc giữa đường thẳng AD và A'C' là
45°.
60°.
30°.
90°.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ^ (ABCD). Khi đó:
a) ((SAC), (SBD)) = 90°.
b) ((SAC), (SBD)) = 45°.
c) (SAB) ^ (SBC).
d) (SCD) ^ (SAD).
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(A\) và \(SA \bot (ABC)\). Khi đó:
a) \((SAC) \bot (ABC)\).
b) Gọi \(H\) là hình chiếu của \(A\) trên \(BC\). Khi đó: \((SAH) \bot (SBC)\).
c) \(\left( {AB,SC} \right) = 60^\circ \)
d) Gọi \(K\) là hình chiếu của \(A\) trên \(SC\). Khi đó: \(\left( {(ABK),(SBC)} \right) = 60^\circ \).
Cho hình lập phương ABCD.A'B'C'D' cạnh a như hình vẽ dưới đây. Xét tính đúng, sai của các khẳng định sau:
a) AA' ^ (ABCD).
b) AC ^ B'D'.
c) Góc giữa hai đường thẳng BA' và CD bằng 45°.
d) Diện tích hình chiếu vuông góc của tam giác A'BC' lên mặt phẳng (ABCD) bằng a2.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H và K lần lượt là trung điểm của AB và CD. Khi đó:
a) AD ^ (SAB).
b) SA ^ CD.
c) ((SAB), (SCD)) = 90°.
d) SH ^ (ABCD).
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = AA' = 2a. Khi đó:
a) Góc giữa mặt phẳng (A'BC) và mặt phẳng (ABC) là \(\widehat {ABA'}\).
b) AA' ^ (ABC).
c) AB ^ (ACC'A').
d) AA' ^ BC.
PHẦN II. TRẢ LỜI NGẮN
Một khối gỗ có dạng hình hộp chữ nhật ABCD.A'B'C'D'. Biết rằng AB = 10 cm, BC = 15 cm và góc giữa hai mặt phẳng (BCD'A'), (ABCD) bằng 30°. Tổng diện tích tất cả các mặt của khối gỗ đó đạt bao nhiêu cm2? Kết quả làm tròn đến hàng đơn vị.
Cho hình chóp cụt tứ giác đều có cạnh đáy nhỏ là 1 cm, cạnh đáy lớn là 2 cm và chiều cao là 3 cm. Tính độ dài cạnh bên (kết quả làm tròn đến hàng phần mười).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Khi đó góc giữa hai mặt phẳng (SAB) và (SAC) bằng bao nhiêu độ?
Cho hình hộp chữ nhật ABCD.A'B'C'D', BC = a, AC = 2a, \(A'A = a\sqrt 3 \). Góc giữa mặt phẳng (BCD'A') và mặt phẳng (ABCD) bằng bao nhiêu độ?
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, BA = BC = a, cạnh bên \(AA' = a\sqrt 2 \). Gọi φ là góc hợp bởi ((A'BC), (ABC)). Khi đó \(\tan \varphi = \sqrt a \). Tìm a.
