22 câu Trắc nghiệm Toán 11 Cánh diều Bài tập cuối chương VI (Đúng-sai, trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hai hàm số f(x) = ax và g(x) = logax. Với 0 < a < 1, chọn khẳng định đúng trong các khẳng định sau:
f(x) nghịch biến và g(x) đồng biến trên tập xác định.
f(x) đồng biến và g(x) nghịch biến trên tập xác định.
f(x) và g(x) đồng biến trên tập xác định.
f(x) và g(x) nghịch biến trên tập xác định.
Với a là số thực dương tùy ý, \({\log _2}\frac{{{a^4}}}{4}\) bằng
−2 + 4log2a.
\(4{\log _2}\frac{a}{4}\).
log2a.
2 – 4log2a.
Cho các số thực dương a, b. Mệnh đề nào sau đây đúng?
\({\log _2}\frac{{2\sqrt[3]{a}}}{{{b^3}}} = 1 + \frac{1}{3}{\log _2}a - \frac{1}{3}{\log _2}b\).
\({\log _2}\frac{{2\sqrt[3]{a}}}{{{b^3}}} = 1 + \frac{1}{3}{\log _2}a - 3{\log _2}b\).
\({\log _2}\frac{{2\sqrt[3]{a}}}{{{b^3}}} = 1 + \frac{1}{3}{\log _2}a + 3{\log _2}b\).
\({\log _2}\frac{{2\sqrt[3]{a}}}{{{b^3}}} = 1 + \frac{1}{3}{\log _2}a + \frac{1}{3}{\log _2}b\).
Tìm tập xác định D của hàm số y = log(x2 + 2x + 3).
D = Æ.
D = ℝ\{−2; −1}.
D = ℝ.
D = (−∞; −2) È (−1; +∞).
Biểu thức \(\sqrt[3]{{a\sqrt {{a^5}} }}\left( {a > 0} \right)\) được viết dưới dạng lũy thừa là
\({a^{\frac{3}{{10}}}}\).
\({a^{\frac{5}{6}}}\).
\({a^{\frac{7}{6}}}\).
\({a^{\frac{7}{{10}}}}\).
Phương trình log(54 – x3) = 3logx có nghiệm là
x = 2.
x = 4.
x = 1.
x = 3.
Tập nghiệm S của bất phương trình log2(2x + 4) ≥ 0 là
\(S = \left[ { - \frac{3}{2}; + \infty } \right)\).
\(S = \left( { - \frac{3}{2}; + \infty } \right)\).
S = [−2; +∞).
(−2; +∞).
Cho bất phương trình \({\left( {\frac{2}{3}} \right)^{{x^2} - x + 1}} > {\left( {\frac{2}{3}} \right)^{2x - 1}}\) có tập nghiệm S = (a; b). Giá trị của b – a bằng
−2.
1.
−1.
2.
Khẳng định nào sai?
1,32 > 1,31,5.
0,9−3 > 0,9−2.
log0,254 < log0,2520.
log35 < 3log32.
Cho x, y là các số thực dương thỏa mãn \({\log _{25}}\frac{x}{2} = {\log _{15}}y = {\log _9}\frac{{x + y}}{4}\) và \(\frac{x}{y} = \frac{{ - a + \sqrt b }}{2}\) với a, b là các số nguyên dương. Tính a + b.
a + b = 14.
a + b = 3.
a + b = 21.
a + b = 34.
Áp suất khí quyển p (tính bằng kilopascal, viết tắt là kPa) ở độ cao h (so với mực nước biển, tính bằng km) được tính theo công thức sau: \(\ln \left( {\frac{p}{{100}}} \right) = - \frac{h}{7}\). Tính áp suất khí quyển ở độ cao 4 km.
p ≈ 50,75 kPa.
p ≈ 56,47 kPa.
p ≈ 45,75 kPa.
p ≈ 55,75 kPa.
Bác Bon gửi tiết kiệm 500 triệu đồng ở một ngân hàng với lãi suất không đổi 7,5%/năm theo hình thức lãi kép. Tổng số tiền bác Bon thu được (cả vốn lẫn lãi) sau n năm là A = 500.(1 + 0,075)n (triệu đồng). Tính thời gian tối thiểu gửi tiết kiệm để bác Bon thu được ít nhất 800 triệu đồng (cả vốn lẫn lãi).
8 năm.
9 năm.
10 năm.
7 năm.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số y = f(x) = log0,5x.
a) Tập xác định của hàm số là D = ℝ.
b) Hàm số đồng biến trên ℝ.
c) Đồ thị hàm số có dạng như hình bên dưới
d) Tập nghiệm của bất phương trình f(x) ≥ −2 là [4; +∞).
Cho bất phương trình log(x – 40) + log(60 – x) ≤ 2.
a) Bất phương trình trên tương đương với log[(x – 40)(60 – x)] ≤ 2.
b) Gọi D = (a; b) là tập xác định của bất phương trình trên thì b – a = 20.
c) Có 19 số nguyên dương thỏa mãn bất phương trình trên.
d) Tập nghiệm của bất phương trình trên chứa 8 số tự nhiên chẵn.
Câu 3. Cho log23 = a; log252 = b. Khi đó:
a) \({\log _2}25 = \frac{1}{b}\).
b) \({\log _2}75 = a + \frac{1}{b}\).
c) log2(3.9) = 9a.
d) Nếu x; y là các số nguyên tố thỏa mãn \({\log _{48600}}25 = \frac{1}{{xab + yb + z}}\) thì x + y + z = 10.
Giá trị của một ngôi nhà sau khi xây n năm được cho bởi công thức V = 6250.ean (triệu đồng) với a là một hệ số xác định. Biết khi n = 3 thì V = 8750 (triệu đồng).
a) Giá trị ban đầu của ngôi nhà là 6250000000 đồng.
b) Giá trị của a là a = 0,112 (làm tròn kết quả đến 3 chữ số sau dấy phẩy).
c) Giá trị của ngôi nhà sau 5 năm là 11000 triệu đồng (làm tròn kết quả đến hàng đơn vị).
d) Sau ít nhất 6 năm thì giá trị ngôi nhà sẽ tăng gấp đôi.
Cho hàm số f(x) = 2x và g(x) = log3(−x2 + 3). Khi đó:
a) Đồ thị của hàm số f(x) là hình dưới đây
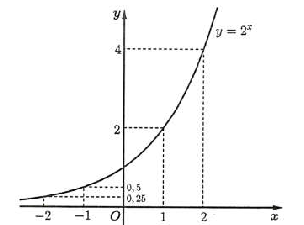
b) Hàm số g(x) có tập xác định \(D = \left( { - \sqrt 3 ;\sqrt 3 } \right)\).
c) x = 2 là nghiệm của phương trình f(x) = 8x – 2.
d) Bất phương trình g(x) > log32x có tập nghiệm S = (−3; 1).
PHẦN II. TRẢ LỜI NGẮN
Cho phương trình \({2^{{x^2}}}{.3^{x + 1}} = 2\). Tính tổng các nghiệm của phương trình (kết quả làm tròn đến một chữ số thập phân).
Chất phóng xạ polonium-210 có chu kì bán rã 138 ngày. Điều này có nghĩa là cứ sau 138 ngày, lượng polomium còn lại trong mẫu chỉ bằng một nửa lượng ban đầu. Một mẫu khối lượng 100 g có khối lượng polonium – 210 còn lại sau t ngày được tính theo công thức \(M\left( t \right) = 100.{\left( {\frac{1}{2}} \right)^{\frac{t}{{138}}}}\) (g). Sau x ngày (x Î ℤ) thì khối lượng polonium-210 còn lại nhỏ hơn 10 g. Tìm giá trị lớn nhất của x.
Số lượng của một loài vi khuẩn sau x giờ được tính bởi công thức f(x) = Aerx, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0). Biết số vi khuẩn ban đầu là 1000 con và sau 10 giờ tăng trưởng thành 5000 con. Tính tỉ lệ tăng trưởng của vi khuẩn (làm tròn đến chữ số phần trăm).
Tìm giá trị của tham số m để phương trình \({\left( {\frac{1}{5}} \right)^{{x^2} - \left( {m + 2} \right)x}} = {5^{27}}\) có hai nghiệm phân biệt a và b thỏa mãn điều kiện \({\log _a}\left( {{b^{{{\log }_a}b}}} \right) - 2{\log _{\sqrt a }}b + 4 = 0\).
Bạn An gửi tiết kiệm vào ngân hàng với lãi suất 1%/tháng (không kỳ hạn). Hỏi bạn An phải gửi ít nhất bao nhiêu tháng thì được cả vốn lẫn lãi gấp đôi số tiền ban đầu?
Cho log23 = a; log252 = b. Khi đó:
a) \({\log _2}25 = \frac{1}{b}\).
b) \({\log _2}75 = a + \frac{1}{b}\).
c) log2(3.9) = 9a.
d) Nếu x; y là các số nguyên tố thỏa mãn \({\log _{48600}}25 = \frac{1}{{xab + yb + z}}\) thì x + y + z = 10.
