12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho dãy (un) có limun = 3, dãy (vn) có limvn = 5. Tính lim(un.vn).
15.
8.
5.
3.
Tìm dạng hữu tỉ của số thập phân vô hạn tuần hoàn P = 2,13131313….
\(P = \frac{{212}}{{99}}\).
\(P = \frac{{213}}{{100}}\).
\(P = \frac{{211}}{{100}}\).
\(P = \frac{{211}}{{99}}\).
Cho \(\lim \frac{{a{n^2} - 4n + 7}}{{5{n^2} - n - 2}} = 6\). Khẳng định nào đúng.
a = 6.
a = 3.
a = 30.
a = 11.
Cho giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = 2;\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 3\). Tính \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {3f\left( x \right) - 4g\left( x \right)} \right]\).
5.
2.
−6.
3.
Tính giới hạn \(L = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{x + 3}}\).
−∞.
0.
+∞.
1.
Trong bốn giới hạn sau đây, giới hạn nào bằng −∞?
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 3x + 4}}{{x - 2}}\).
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 3x + 4}}{{x - 2}}\).
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - 3x + 4}}{{x - 2}}\).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 3x + 4}}{{x - 2}}\).
Cho \(I = \mathop {\lim }\limits_{x \to 0} \frac{{2\left( {\sqrt {3x + 1} - 1} \right)}}{x}\) và \(J = \mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} - x - 2}}{{x + 1}}\). Tính I – J.
6.
3.
−6.
0.
Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {2{x^3} - {x^2} + 1} \right)\).
+∞.
−∞.
2.
0.
Cho \(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt {3x + 4} - 4}}{{x - 4}} = \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính 2a + b2.
22.
66.
14.
70.
Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm nào?
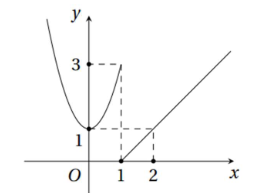
x = 0.
x = 1.
x = 2.
x = 3.
Hàm số nào sau đây không liên tục tại x = 2?
\(y = \sqrt {x + 2} \).
y = x2.
\(y = \frac{{{x^2}}}{{x - 2}}\).
y = x2 – 3x + 2.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} + 3x - 4}}{{x - 1}}\;\;khi\;x \ne 1\\m - 2\;\;\;\;\;\;\;\;\;\;khi\;x = 1\end{array} \right.\). Giá trị nào của m thì hàm số đã cho liên tục trên ℝ.
m = 4.
m = 7.
m = 8.
m = 2.
