22 câu Trắc nghiệm Toán 11 Cánh diều Bài tập cuối chương II (Đúng-sai, trả lời ngắn) có đáp án

PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI

Cho dãy số (u_n) có số hạng tổng quát \({u_n} = \frac{{n + 1}}{{n + 2}}\).

a) \({u_{n + 1}} - {u_n} = \frac{1}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\).

b) u_{n + 1} < u_n, ∀n ∈ ℕ*.

c) Dãy số (u_n) là dãy số giảm.

d) Dãy (u_n) là dãy số bị chặn.

Anh An đang tập đầu tư chứng khoán. Ở cuối mỗi lần đầu tư, anh An hoặc mất hết tiền đã đầu tư hoặc lời bằng số tiền đã bỏ ra. Ví dụ nếu anh An đầu tư a đồng, anh An sẽ mất a đồng nếu lỗ và sẽ có a đồng tiền lãi nếu lời.

Lần đầu tiên anh đầu tư 20000 đồng, mỗi lần sau tiền đầu tư gấp đôi lần trước. Anh An lỗ 9 lần liên tiếp và lời ở lần thứ 10.

a) Số tiền đầu tư lần thứ hai là 400000 đồng.

b) Số tiền anh An lỗ lần thứ 9 là 5120000 đồng.

c) Số tiền đã thua trong 5 lần đầu là 620000 đồng.

d) Sau lần thứ 10 thì anh An hòa vốn.

Một khán đài của sân vận động A có n hàng ghế, số ghế mỗi hàng trên đều hơn số ghế mỗi hàng dưới kề nó là 50 ghế; số ghế hàng trên cùng gấp đôi số ghế hàng dưới cùng của khán đài; tổng số ghế của 2 hàng trên cùng là 1550 ghế. Gọi u_n là số ghế hàng thứ n.

a) Khán đài có 9 hàng ghế.

b) (u_n) là một cấp số cộng có công sai d = 50.

c) u₁ = 2u_n.

d) Sức chứa của khán đài là 4500 chỗ ngồi.

Cho cấp số nhân (u_n) thỏa mãn \({u_2} = \frac{3}{4};{u_3} = \frac{{ - 3}}{8}\).

a) Số hạng đầu \({u_1} = - \frac{3}{2}\) và công bội \(q = \frac{1}{2}\).

b) (u_n) là dãy số tăng.

c) Số hạng tổng quát là \({u_n} = - \frac{3}{2}{\left( { - \frac{1}{2}} \right)^{n - 1}}\left( {n \in \mathbb{N}*} \right)\).

d) Số hạng \({u_5} = - \frac{3}{{32}}\).

Một ruộng bậc thang có thửa ruộng thấp nhất (bậc thứ nhất) nằm ở độ cao 600 m so với mực nước biển, độ chênh lệch giữa thửa trên và thửa dưới trung bình là 1,1 m. Kí hiệu u_n là chiều cao của thửa ruộng ở bậc thứ n so với mực nước biển (đơn vị là mét).

a) u₁ =601,1.

b) (u_n) là một cấp số cộng với công sai d = 1,1.

c) Thửa ruộng ở bậc thứ 8 có chiều cao so với mực nước biển là 608,8 m.

d) Tổng chiều cao 50 m thửa ruộng đầu tiên so với mực nước biển bằng 31347,5 m.

PHẦN II. TRẢ LỜI NGẮN

 Một em học sinh dùng các que diêm để xếp thành hình tháp có quy luật được thể hiện như trong hình sau:

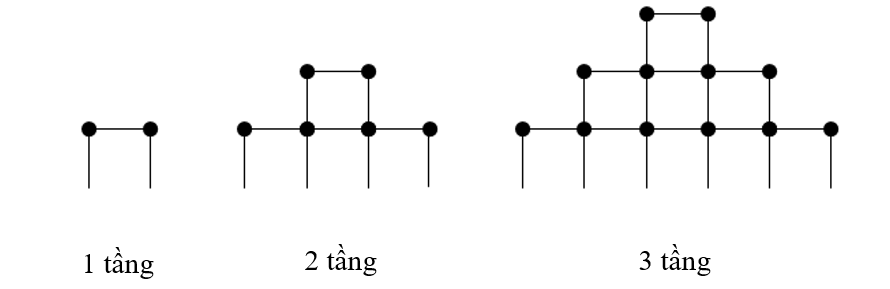
Hỏi cần bao nhiêu que diêm để xếp thành hình tháp có \(10\) tầng?

Tìm \(x\) để các số \(2;8;x;128\) theo thứ tự đó lập thành một cấp số nhân.

Cho cấp số cộng (u_n) thỏa mãn \(\left\{ \begin{array}{l}{u_3} - {u_4} + {u_5} = 7\\{u_1} + {u_6} = 12\end{array} \right.\). Số 11 là số hạng thứ bao nhiêu của cấp số cộng trên.

Các nhà nghiên cứu đã chỉ ra công thức tính cân nặng lí tưởng theo tuổi ở trẻ em từ 2 tuổi đến 12 tuổi là u_n = 2n + 8, trong đó n là số tuổi của trẻ và u_n là cân nặng lí tưởng đơn vị kilôgam. Hỏi theo công thức trên thì cân nặng lí tưởng của trẻ 6 tuổi là bao nhiêu kilôgam?

Trong hội chợ, một công ty sơn muốn xếp 1089 hộp sơn theo số lượng 1; 3; 5; … từ trên xuống. Hàng cuối cùng có bao nhiêu hộp sơn?