22 câu Trắc nghiệm Toán 11 Cánh diều Bài tập cuối Chương 1 (Đúng sai, trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Với mọi số thực \(\alpha \), ta có \(\sin \left( {\frac{{9\pi }}{2} + \alpha } \right)\) bằng
\( - {\mkern 1mu} \sin \alpha .\)
\(\cos \alpha .\)
\(\sin \alpha .\)
\( - {\mkern 1mu} \cos \alpha .\)
Trên đường tròn lượng giác có điểm gốc là \(A\). Điểm \(M\)thuộc đường tròn sao cho cung lượng giác \(AM\) có số đo \(45^\circ \). Gọi \(N\) là điểm đối xứng với \(M\) qua trục \(Ox\), số đo cung lượng giác \(AN\) bằng
\( - \,\,45^\circ \).
\(315^\circ \).
\(45^\circ \) hoặc \(315^\circ \).
\( - \,\,45^\circ + k360^\circ ,k \in \mathbb{Z}\).
Đơn giản biểu thức \(A = \cos \left( {\alpha - \frac{\pi }{2}} \right) + \sin (\alpha - \pi )\), ta được
\(A = \cos \alpha + \sin \alpha .\)
\(A = 2\sin \alpha .\)
\(A = \sin \alpha \cos \alpha .\)
\(A = 0.\)
Khẳng định nào sau đây đúng?
\(\sin \left( {2018a} \right) = 2018\sin a.\cos a.\)
\(\sin \left( {2018a} \right) = 2018\sin \left( {1009a} \right).\cos \left( {1009a} \right).\)
\(\sin \left( {2018a} \right) = 2\sin a\cos a.\)
\(\sin \left( {2018a} \right) = 2\sin \left( {1009a} \right).\cos \left( {1009a} \right).\)
Cho \(0 < \alpha ,{\rm{ }}\beta < \frac{\pi }{2}\) và thỏa mãn \(\tan \alpha = \frac{1}{7}\), \(\tan \beta = \frac{3}{4}\). Góc \(\alpha + \beta \) có giá trị bằng
\(\frac{\pi }{3}.\)
\(\frac{\pi }{4}.\)
\(\frac{\pi }{6}.\)
\(\frac{\pi }{2}.\)
Tính giá trị của biểu thức \(M = \cos \frac{{2\pi }}{7} + \cos \frac{{4\pi }}{7} + \cos \frac{{6\pi }}{7}.\)
\(M = 0\).
\(M = - \frac{1}{2}\).
\(M = 1\).
\(M = 2\).
Mệnh đề nào sau đây là sai?
Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi .\)
Hàm số \[y = \tan x\] tuần hoàn với chu kì \(2\pi .\)
Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi .\)
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = 3\sin x - 2.\)
\(M = 1,{\rm{ }}m = - 5.\)
\(M = 3,{\rm{ }}m = 1.\)
\(M = 2,{\rm{ }}m = - 2.\)
\(M = 0,{\rm{ }}m = - 2.\)
Tìm tập xác định \(D\) của hàm số \(y = \sqrt {\sin x - 2} .\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}.\)
\(D = \left[ { - 1;1} \right].\)
\(D = \emptyset .\)
Nghiệm của phương trình \[{\cos ^2}x = 0\] là:
\(x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình \(\sqrt 3 + 3\tan x = 0\) là:
\(x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Tổng tất cả các nghiệm của phương trình \[\cos \left( {\sin x} \right) = 1\] trên \[\left[ {0;2\pi } \right]\] bằng:
\[0\].
\[\pi \].
\[2\pi \].
\[3\pi \].
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho biết \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \).
a) \(\cos \alpha > 0\).
b) \(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
c) \(\sin 2\alpha = \frac{{ - \sqrt 3 }}{2}\).
d) \(\cos 2\alpha = \sin \alpha \).
Cho tam giác \(ABC\) có ba góc \(A\),\(B\),\(C\) thỏa mãn \(\sin A = \cos B + \cos C\)
a) Tam giác \(ABC\) có \(\frac{{B + C}}{2} = \frac{\pi }{2} - \frac{A}{2}\).
b) \(\cos \frac{{B + C}}{2} = \cos \frac{A}{2}\).
c) \(\sin A = \cos B + \cos C \Leftrightarrow \cos \frac{A}{2} = \cos \frac{{B - C}}{2}\).
d) Tam giác \(ABC\) là tam giác cân.
Cho phương trình \(\sin \left( {2x - \frac{\pi }{4}} \right) = \sin \left( {x + \frac{{3\pi }}{4}} \right)\) (*).
a) Phương trình có nghiệm: \(x = \pi + k2\pi \) và \(x = \frac{\pi }{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{7\pi }}{6}\).
d) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có nghiệm lớn nhất bằng \(\frac{{5\pi }}{6}\).
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*).
a) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\).
b) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\).
d) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\).
Một vật dao động xung quanh vị trí cân bằng theo phương trình \(x = 1,5\cos \left( {\frac{{t\pi }}{4}} \right)\); trong đó \(t\) là thời gian được tính bằng giây và quãng đường \(h = \left| x \right|\) được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng (xem hình bên).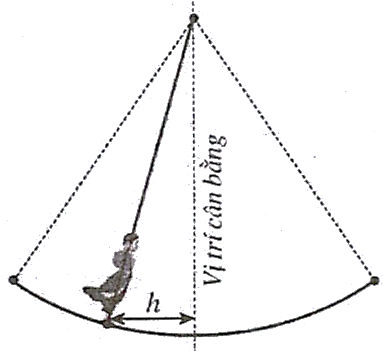
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;\,{\rm{m}}\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\).
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
PHẦN III. TRẢ LỜI NGẮN
Trong một buổi biểu diễn ở rạp xiếc, người nghệ sĩ có một tiết mục giữ thăng bằng và đạp xe 1 bánh trên 1 sợi dây dài \(30\,\,{\rm{m}}\). Hỏi khi người nghệ sĩ đi hết đoạn dây thì bán kính xe đạp quét một góc lượng giác có số đo là bao nhiêu radian? Biết bánh xe đạp có bán kính bằng \(0,4\,\,{\rm{m}}\).

Một vận động viên bắn súng nằm trên mặt đất để gắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất \(25\,\,\left( {\rm{m}} \right)\) tại một góc ngắm (góc hợp bởi phương ngắm với phương ngang). Nếu giảm góc ngắm đi một nửa thì vận động viên bắn trúng mục tiêu cách mặt đất \(10\,\,\left( {\rm{m}} \right)\). Khoảng cách từ vận động viên đến bức tường bằng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Cho \[2\tan a - \cot a = 1\]với \[ - \frac{\pi }{2} < a < 0\]. Tính giá trị biểu thức \[P = \frac{{\tan \left( {6\pi - a} \right) - 2\cot \left( {3\pi + a} \right)}}{{3\tan \left( {\frac{{3\pi }}{2} + a} \right)}}\] (viết kết quả dưới dạng số thập phân).
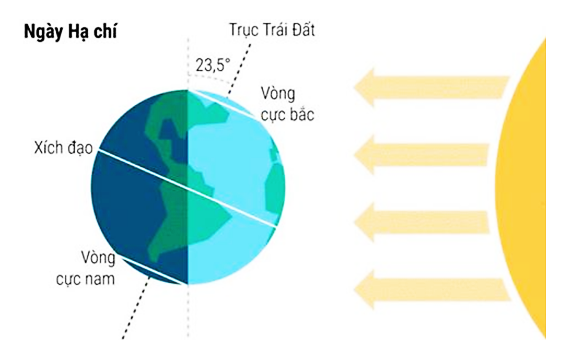
Ngày Hạ Chí chỉ khoảng thời gian bắt đầu mùa hè tại Bắc bán cầu và mùa đông ở Nam bán cầu. Hiện tượng này xảy ra khi một trong hai cực của Trái Đất có độ nghiêng tối đa về phía Mặt Trời. Vào ngày hạ chí, Trái Đất sẽ nhận lượng bức xạ lớn, thời gian ngày dài hơn đêm, trời lâu tối và nhanh sáng. Thậm chí, một số thành phố ở Bắc Âu còn có hiện tượng đêm trắng, tức là hoàn toàn không có ban đêm. Số giờ có ánh sáng của thành phố \(A\) trong ngày thứ \(t\) của một năm không nhuận được cho bởi hàm số \(d\left( t \right){\kern 1pt} \, = \,3\sin \left[ {\frac{\pi }{{182}}\left( {t - 180} \right) + 12} \right]\) với\(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An đến thành phố \(A\)và được biết hôm ấy là ngày Hạ Chí, ngày có nhiều ánh sáng mặt trời nhất trong năm của thành phố đó. Hỏi An đến thành phố \(A\) vào ngày nào trong năm?
Cho phương trình \(\cos 5x = \cos \left( {x + \frac{\pi }{4}} \right)\). Tìm số nghiệm thuộc đoạn \(\left[ { - 2024;2024} \right]\) của phương trình đã cho.
