22 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Phương trình lượng giác cơ bản (Đúng-sai, trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Nghiệm của phương trình \(\sin 2x = 1\) là
\(x = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{k\pi }}{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
Tìm tất cả các giá trị thực của tham số \[m\] để phương trình \[\sin x = m\] có nghiệm.
\(m \le 1\).
\(m \ge - 1\).
\( - 1 \le m \le 1\).
\(m \le - 1\).
Nghiệm của phương trình \[\cot x + \sqrt 3 \; = {\rm{ }}0\] là:
\(x = \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Tập nghiệm của phương trình \[\sin 2x = \sin x\] là
\[S = \left\{ {k2{\rm{\pi }};\frac{{\rm{\pi }}}{3} + k2{\rm{\pi }}\left| {k \in \mathbb{Z}} \right.} \right\}\].
\[S = \left\{ {k2{\rm{\pi }};\frac{{\rm{\pi }}}{3} + \frac{{k2{\rm{\pi }}}}{3}\left| {k \in \mathbb{Z}} \right.} \right\}\].
\[S = \left\{ {k2{\rm{\pi }}; - \frac{{\rm{\pi }}}{3} + k2{\rm{\pi }}\left| {k \in \mathbb{Z}} \right.} \right\}\].
\[S = \left\{ {k2{\rm{\pi }};{\rm{\pi }} + k2{\rm{\pi }}\left| {k \in \mathbb{Z}} \right.} \right\}\].
Phương trình \(\sin 2x = \cos x\) có nghiệm là
\(\left[ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k\pi }}{3}\\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
\(\left[ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k\pi }}{3}\\x = \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
\(\left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
\(\left[ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k2\pi }}{3}\\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Giải phương trình \(\sqrt {\rm{3}} \tan 2x - 3 = 0\).
\(x = \frac{\pi }{3} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{6} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Phương trình lượng giác \(3\cot \,x - \sqrt 3 = 0\) có nghiệm là:
\[x = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Vô nghiệm.
Phương trình lượng giác \(\cos 3x = \cos 12^\circ \) có nghiệm là
\[x = \pm \frac{\pi }{{15}} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \pm \frac{\pi }{{45}} + \frac{{k2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{{ - \pi }}{{45}} + \frac{{k2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{{45}} + \frac{{k2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\].
Giải phương trình lượng giác \(2\cos \frac{x}{2} + \sqrt 3 = 0\) có nghiệm là:
\(x = \pm \frac{{5\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{{5\pi }}{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{{5\pi }}{6} + k4\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{{5\pi }}{3} + k4\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Tìm tất cả các giá trị thực của tham số \[m\] để phương trình \[\cos x - m = 0\] vô nghiệm.
\(m \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
\(m \in \left( {1; + \infty } \right)\).
\(m \in \left[ { - 1;1} \right]\).
\(m \in \left( { - \infty ; - 1} \right)\).
Số nghiệm của phương trình \({\rm{sin}}\left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
4.
1.
2.
3.
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\cos 2x + \sin x + m = 0\) có nghiệm \(x \in \left[ { - \frac{\pi }{6};\frac{\pi }{4}} \right]\)?
2.
1.
0.
3.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho phương trình \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\).
a) Phương trình đã cho tương đương với phương trình \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( {\frac{\pi }{3}} \right)\).
b) Phương trình đã cho có nghiệm là: \(x = \frac{\pi }{4} + k2\pi ;\,\,x = \frac{{7\pi }}{{12}} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Phương trình đã cho có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\).
d) Số nghiệm của phương trình đã cho trong khoảng \(\left( { - \pi ;\pi } \right)\) là hai nghiệm.
Cho phương trình \(\sqrt 2 \cos \left( {2x + \frac{\pi }{4}} \right) - 1 = 0\,\,\,\,\left( 1 \right)\)
a) Phương trình \(\left( 1 \right) \Leftrightarrow \cos \left( {2x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right)\,.\)
b) Phương trình \(\left( 1 \right)\) có nghiệm \(x = k2\pi ;x = - \frac{\pi }{4} + k2\pi \left( {k \in \mathbb{Z}} \right).\)
c) Trên khoảng \(\left( {0;\pi } \right)\) phương trình \(\left( 1 \right)\) có tập nghiệm là \(S = \left\{ {\frac{{3\pi }}{4}} \right\}.\)
d) Tổng các nghiệm của phương trình \(\left( 1 \right)\) trong khoảng \(\left( { - 3\pi ;3\pi } \right)\) là \(3\pi .\)
Cho hàm số \(y = \sin \left( {x - \frac{\pi }{4}} \right)\) và hàm số\(y = \cos \left( {\frac{\pi }{2} - x} \right)\).
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho \(\sin \left( {x - \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{2} - x} \right)\).
b) Hoành độ giao điểm của hai đồ thị hàm số đã cho là \(x = \frac{{5\pi }}{8} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
c) Điểm \(M\left( {\frac{{5\pi }}{8};\sin \frac{{5\pi }}{8}} \right)\) là một giao điểm của hai đồ thị hàm số đã cho trên \(\left[ {0\,;2\pi } \right]\).
d) Khi \(x \in \left[ {0\,;3\pi } \right]\) thì hai đồ thị hàm số đã cho cắt nhau tại ba điểm lần lượt \[A,B,C\]gọi \[I\]là trung điểm của \[AC\]thì \[I\left( {\frac{{13\pi }}{{16}};\sin \left( {\frac{{13\pi }}{4}} \right)} \right)\].
Cho phương trình \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
a) Hạ bậc hai vế, ta được phương trình \(\frac{{1 + \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 - \cos \left( {2x + \pi } \right)}}{2}\).
b) Ta có \(\cos \left( {2x + \pi } \right) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và
Cho phương trình \(\tan \left( {2x - 15^\circ } \right) = 1\) (*).
a) Phương trình (*) có nghiệm \(x = 30^\circ + k90^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
b) Phương trình có nghiệm âm lớn nhất bằng \( - 30^\circ \).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\) bằng \(180^\circ \).
d) Trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\), phương trình có nghiệm lớn nhất bằng \(60^\circ \).
PHẦN III. TRẢ LỜI NGẮN
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu \[h\,\,\left( {\rm{m}} \right)\]của mực nước trong kênh tính theo thời gian \[t\left( h \right)\]được cho bởi công thức \[h = 3\sin \left( {\frac{{\pi t}}{4} + \frac{\pi }{3}} \right) + 14\]. Thời gian ngắn nhất để mực nước của kênh cao nhất là \[t = \frac{a}{b}\]. Tính \[a.b\]?
Số giờ có ánh sáng mặt trời của một thành phố \(A\) trong ngày thứ \(t\) (ở đây \(t\) là số ngày tính từ ngày 1 tháng 1) của năm \(2024\) được cho bởi hàm số \(f\left( t \right) = 12 + 2,83\sin \left( {\frac{\pi }{{182}}\left( {t - 80} \right)} \right)\), \[t \in {\mathbb{N}^*}\] và \(0 < t \le 366\). Hỏi vào ngày nào trong tháng 6 thì thành phố \(A\) có nhiều giờ có ánh sáng mặt trời nhất?
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình\(x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\).
Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Một cái cổng vào một trung tâm thương mại có hình dạng là một phần của đồ thị hàm số \(y = 2\cos \left( {\frac{x}{2}} \right) + 2\). Gọi \(A,B\) là hai điểm nằm trên cổng (trên đồ thị hàm số \(y = 2\cos \left( {\frac{x}{2}} \right) + 2\)) và \(C,D\) là hai điểm nằm trên mặt nền của cổng sao cho \(ABCD\) là hình chữ nhật. Người quản lí trung tâm thương mại muốn lắp một cái cửa kính tự động vào hình chữ nhật \(ABCD\). Tính diện tích của cái cửa cần lắp biết chiều cao của cái cửa là \(AD = 3\) mét (kết quả làm tròn đến một chữ số thập phân theo đơn vị mét vuông, lấy \(\pi = 3,14\)).
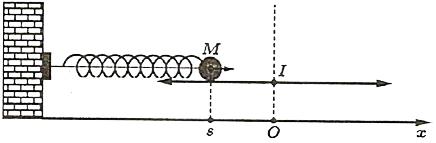
Một vật \(M\) được gắn vào đầu lò xo và dao động quanh vị trí cân bằng \(I\), biết rằng \(O\) là hình chiếu vuông góc của \(I\) trên trục \(Ox\), toạ độ điểm \(M\) trên \(Ox\) tại thời điểm \(t\) (giây) là đại lượng \(s\) (đơn vị: cm) được tính bởi công thức \(s = 8,6\cos \left( {8t + \frac{\pi }{2}} \right)\). Tại mấy thời điểm trong khoảng 2 giây đầu tiên thì \(s = 4,3\;\) cm?