22 câu Trắc nghiệm Toán 11 Cánh diều Bài 1. Góc lượng giác. Giá trị lượng giác của góc lượng giác (Đúng-sai, trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Quy ước chọn chiều dương của một đường tròn định hướng là:
Luôn cùng chiều quay kim đồng hồ.
Luôn ngược chiều quay kim đồng hồ.
Có thể cùng chiều quay kim đồng hồ mà cũng có thể là ngược chiều quay kim đồng hồ.
Không cùng chiều quay kim đồng hồ và cũng không ngược chiều quay kim đồng hồ.
Khẳng định nào sau đây là đúng?
\(\pi {\rm{ rad }} = 1^\circ .\)
\(\pi {\rm{ rad }} = 60^\circ .\)
\(\pi {\rm{ rad }} = 180^\circ .\)
\(\pi {\rm{ rad }} = \left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array}.\)
Đổi số đo của góc \( - \frac{{3\pi }}{{16}}{\rm{ rad}}\) sang đơn vị độ, phút, giây.
\(33^\circ 45'.\)
\( - 29^\circ 30'.\)
\( - 33^\circ 45'.\)
\( - 32^\circ 55.\)
Cho \(\pi < \alpha < \frac{{3\pi }}{2}.\) Khẳng định nào sau đây đúng?
\(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) < 0.\)
\(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) > 0.\)
\(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) \le 0.\)
\(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) \ge 0.\)
Cho bốn cung (trên một đường tròn định hướng): \[\alpha = - \frac{{5\pi }}{6},\] \[\beta = \frac{\pi }{{\rm{3}}}\], \[\gamma = \frac{{{\rm{25}}\pi }}{{\rm{3}}},\] \[\delta = \frac{{{\rm{19}}\pi }}{{\rm{6}}}\]. Các cung nào có điểm cuối trùng nhau?
\[\alpha \] và \[\beta \]; \[\gamma \] và \[\delta \].
\(\beta \) và \[\gamma \]; \[\alpha \] và \[\delta \].
\[\alpha ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma \].
\[\beta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \].
Tính giá trị của \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right].\)
\(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] = - \frac{{\sqrt 3 }}{2}.\)
\(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] = - \frac{{\sqrt 2 }}{2}.\)
\(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] = - \frac{1}{2}.\)
\(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] = \frac{{\sqrt 3 }}{2}.\)
Tính giá trị biểu thức \(P = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .....\tan 80^\circ .\)
\(P = 0.\)
\(P = 1.\)
\(P = 4.\)
\(P = 8.\)
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{2}{3}.\)
\( - \frac{1}{3}.\)
\(\frac{1}{3}.\)
\(\frac{2}{3}.\)
Biết \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) là các góc của tam giác \[ABC,\]mệnh đề nào sau đây đúng:
\(\sin \left( {A + C} \right) = - {\mkern 1mu} \sin B.\)
\(\cos \left( {A + C} \right) = - {\mkern 1mu} {\mkern 1mu} \cos B.\)
\(\tan \left( {A + C} \right) = \tan B.\)
\(\cot \left( {A + C} \right) = \cot B.\)
Cho góc \(\alpha \) thỏa mãn \({\rm{cot}}\alpha = \frac{1}{3}.\) Tính \(P = \frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}.\)
\(P = - \frac{{15}}{{13}}.\)
\(P = \frac{{15}}{{13}}.\)
\(P = - 13.\)
\(P = 13.\)
Biểu thức lượng giác \({\left[ {\sin \left( {\frac{\pi }{2} - x} \right) + \sin \left( {10\pi + x} \right)} \right]^2} + {\left[ {\cos \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {8\pi - x} \right)} \right]^2}\) có giá trị bằng?
\(1.\)
\(2.\)
\(\frac{1}{2}.\)
\(\frac{3}{4}.\)
Cho góc \(\alpha \) thỏa mãn \(\tan \alpha = - \frac{4}{3}\) và \(\frac{{2017\pi }}{2} < \alpha < \frac{{2019\pi }}{2}\). Tính \(\sin \alpha .\)
\(\sin \alpha = - \frac{3}{5}.\)
\(\sin \alpha = \frac{3}{5}.\)
\(\sin \alpha = - \frac{4}{5}.\)
\(\sin \alpha = \frac{4}{5}.\)
a) \(A = \cos \alpha - \sin \alpha \).
b) \(B = \cos \alpha + \tan \alpha \).
c) \(A + B = \frac{{27}}{{20}}\).
d) \(A - B = - \frac{{29}}{{20}}\).
a) \(\cos x > 0\).
b) \(\cos x = - \frac{4}{5}\).
c) \(\tan x = \frac{3}{4}\).
d) \(\cot x = \frac{4}{3}\).
a) \(\sin x < 0\).
b) \(\sin x = - \frac{{\sqrt {15} }}{4}\).
c) \(\tan x = \sqrt {15} \).
d) \(\cot x = - \frac{1}{{\sqrt {15} }}\).
a) \(\sin x < 0\).
b) \(\tan x = \frac{{12}}{5}\).
c) \(\cot x = \frac{5}{{12}}\).
d) \(\sin x - \cos x = - \frac{{12}}{{13}}\).
a) Quãng đường vệ tinh \(X\) chuyển động được sau 1 giờ là: \[ \approx 28902,65\,\,{\rm{(km)}}{\rm{. }}\]
b) Quãng đường vệ tinh \(X\) chuyển động được sau 1,5 giờ là: \( \approx 43353,98\,\,{\rm{(km)}}\).
c) Sau khoảng 5,3 giờ thì \(X\) di chuyển được quãng đường \(240000\;\,{\rm{km}}\).
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc \(\frac{{9\pi }}{2}\)rad?
PHẦN III. TRẢ LỜI NGẮN
Biểu thức \(S = \frac{{\sin \left( {\frac{{15\pi }}{2} - x} \right) - 2\cos \left( {x - \pi } \right)}}{{\cos \left( {\frac{{5\pi }}{2} - x} \right)}} = k\cot x\). Khi đó \(k = ?\)
Cho \[\cos x = \frac{1}{2}\]. Tính giá trị của biểu thức \(P = 3{\sin ^2}x + 4{\cos ^2}x\) và viết kết quả dưới dạng số thập phân.
Cho \[\sin a + \cos a = \frac{1}{3}\] với \[ - \frac{\pi }{2} < a < 0\]. Biết \[A = \sin a - \cos a = - \frac{{\sqrt m }}{n}\] với m là số nguyên tố. Tính\[m + n\]?
Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút (đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy \(\pi = 3,14\)), biết rằng đường kính của bánh xe đạp là \(0,68\,\,{\rm{m}}\).
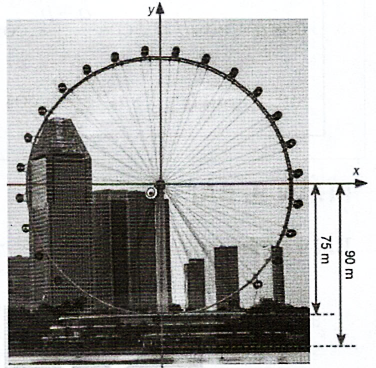
Một chiếc đu quay có bán kính \(75\;\,{\rm{m}}\), tâm của vòng quay ở độ cao \(90\;\,{\rm{m}}\), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?