25 câu hỏi
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong và . Biết 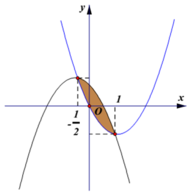
Khi đó diện tích hình phẳng được tô trên hình vẽ là
.
.
.
.
Nguyên hàm của hàm số là
Trong các đẳng thức sau, đẳng thức nào sai?
Cho hàm số f(x) có đạo hàm trên đoạn [1;3], f(1) = 1 và f(3) = 2018. Giá trị của tích phân
I = 2017.
I = -2017.
I = 2018.
I = 2016.
Biết F(x) làm một nguyên hàm của hàm số và F(0) = 2018. Giá trị của F(1) là
F(1) = 2016
Cho hình phẳng (H) giới hạn bới các đường , và . Diện tích S của hình phẳng (H) là
Cho hình phẳng (H) giới hạn bởi các đường y=sinx, , hai trục tọa độ. Thể tích V của khối tròn xoay khi quay (H) quanh trục Ox là
Cho hình phẳng (H) giới hạn bởi các đường , và hai trục tọa độ. Đường thẳng x = k chia (H) thành hai phần có diện tích S1, S2 như hình vẽ bên. Để S1 = 6S2 thì . Hỏi gần giá trị nào nhất trong các giá trị sau?
0,92.
1,24.
1,52.
1,64.
Cho Parapol (P): và đường thẳng (d): . Tìm m để diện tích hình phẳng giới hạn bởi (P) và (d) đạt giá trị nhỏ nhất?
0.
3/4
4/3
1.
Tìm nguyên hàm của hàm số f(x) = sin2x
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b ( như hình bên). Biết và . Hỏi S bằng bao nhiêu?
7
5
2
3
Cho hàm số . Tích phân có giá trị bằng bao nhiêu?
Cho (H) là hình phẳng giới hạn bởi cung tròn có bán kính R=2, đường cong và trục hoành ( miền tô đậm như hình vẽ).
.jpg)
Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
Biết , với a,b,c là các số hữu tỉ. Tính S = a - 3b + c
S = 3
S = 2
S = -2
S = 4
Trong các đẳng thức sau, đẳng thức nào đúng?
Nếu F(x) là một nguyên hàm của hàm số và đồ thị y = F(x) đi qua điểm thì F(x) là
Cho tích phân . Biết kết quả với . Khi đó a-b+c bằng bao nhiêu?
.
.
2.
-2.
Cho a,b là các số thực dương thỏa mãn . Tích phân có giá trị bằng bao nhiêu?
I = 0.
I = 1.
I = |a-b|.
I = e.
Cho hình phẳng (H) giới hạn bởi các đường y = tanx, y = 0; x = 0, . Khi đó thể tích V của khối tròn xoay tạo ra khi quay (H) quay quanh trục Ox bằng bao nhiêu?
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong , trục hoành, trục tung và đường thẳng x = 2. Biết thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị gần giá trị nào nhất trong các giá trị sau?
0.
1.
4.
-3.
Bạn Huyền gửi vào ngân hàng 10 triệu đồng trong 10 năm. Có 2 hình thức để lựa chọn.
Hình thức 1: Lãi suất là 5% 1 năm.
Hình thức 2: Lãi suất 1 tháng.
Biết rằng trong suốt thời gian 10 năm lãi suất ngân hàng luôn ổn định theo từng hình thức chọn gửi. Khẳng định nào sau đây là đúng? (số tiền làm tròn đến nghìn đồng)
Cả 2 hình thức có số tiền lãi như sau là 6.289.000 đồng.
Số tiền lãi của hình thức 2 cao hơn 181.000 đồng.
Số tiền lãi của hình thức 1 cao hơn 181.000 đồng.
Cả 2 hình thức có cùng số lãi là 6.470.000 đồng.
Nguyên hàm của hàm số là:
Có với thì là:
14
66
70
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là:
Cho hàm số y = f(x) có đồ thị hình bên thì công thức tính diện tích hình phẳng phần tô đậm trong hình là:

