21 câu Trắc nghiệm Toán 10 Cánh diều Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng (Đúng-sai, trả lời ngắn) có đáp án
21 câu hỏi
Cho hàm số \[y = - {x^2} + 4x + 1\]. Khẳng định nào sau đây sai?
Trên khoảng \[\left( { - \infty ;1} \right)\], hàm số đồng biến.
Hàm số nghịch biến trên khoảng \[\left( {2; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;2} \right)\].
Trên khoảng \[\left( {3; + \infty } \right)\], hàm số nghịch biến.
Hàm số nghịch biến trên khoảng \[\left( {4; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;4} \right)\].
Hàm số \(f\left( x \right) = {x^2} - 2x + 3\) đồng biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( { - 3; + \infty } \right)\).
Cho parabol \(\left( P \right):y = 3{x^2} - 2x + 1\). Điểm nào sau đây là đỉnh của \(\left( P \right)\)?
\(I\left( {0;1} \right)\).
\(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
\(I\left( { - \frac{1}{3};\,\frac{2}{3}} \right)\).
\(I\left( {\frac{1}{3};\, - \frac{2}{3}} \right)\).
Đồ thị nào sau đây là đồ thị của hàm số \[y = {x^2} - 2x - 3\]?
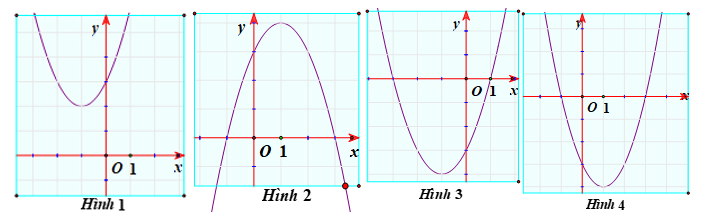
Hình \[1\].
Hình \[2\].
Hình \[3\].
Hình \[4\].
Xác định các hệ số \(a\) và \(b\) để parabol \(\left( P \right):y = a{x^2} + 4x - b\) có đỉnh \(I\left( { - 1; - 5} \right)\).
\(\left\{ \begin{array}{l}a = 3\\b = - 2\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right..\)
Cho hàm số \[y = a{x^2} + bx + c\] có đồ thị như hình bên.
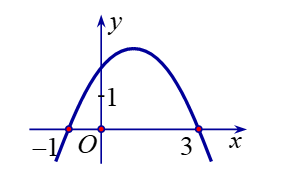
Khẳng định nào sau đây đúng?
\[a > 0\], \[b > 0\], \[c > 0\].
\[a > 0\], \[b < 0\], \[c < 0\].
\[a < 0\], \[b < 0\], \[c > 0\].
\[a < 0\], \[b > 0\], \[c > 0\].
Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
\(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
\(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
\(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
\(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Khẳng định nào dưới đây đúng?
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{{12}}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{{12}}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{3}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{3}\).
Tìm giá trị thực của tham số \(m \ne 0\) để hàm số \(y = m{x^2} - 2mx - 3m - 2\) có giá trị nhỏ nhất bằng \( - 10\) trên \(\mathbb{R}.\)
\(m = 1.\)
\(m = 2.\)
\(m = - 2.\)
\(m = - 1.\)
Gọi \(S\) là tập hợp tất cả các giá trị dương của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = 4{x^2} - 4mx + {m^2} - 2m\) trên đoạn \(\left[ { - 2;\,0} \right]\) bằng \(3\). Tổng \(T\) các phần tử của \(S\) là
\(T = 3\).
\(T = \frac{1}{2}\).
\(T = \frac{9}{2}\).
\(T = - \frac{3}{2}\).
Parabol\(y = a{x^2} + bx + c\) đi qua ba điểm \(A\left( {0; - 1} \right)\), \(B\left( {1; - 1} \right)\), \(C\left( { - 1;1} \right)\) có phương trình là
\(y = {x^2} - x + 1\).
\(y = {x^2} - x - 1\).
\(y = {x^2} + x - 1\).
\(y = {x^2} + x + 1\).
Xét đồ thị của hàm số \(y = {x^2} - 4x - 5\).
a) Có toạ độ đỉnh \(I\left( {2;9} \right)\).
b) Trục đối xứng là \(x = 2\).
c) Giao điểm của đồ thị với trục tung là \(C\left( {0\,; - 5} \right)\).
d) Giao điểm của đồ thị với trục hoành là \(A\left( { - 1\,;0} \right)\) và \(B\left( {5\,;0} \right)\).
Cho parabol \(y = {x^2} - 4x + 3\).
a) Trục đối xứng của đồ thị hàm số là đường thẳng \(x = 2\).
b) Tọa độ đỉnh của parabol là \(I\left( {2; - 3} \right)\).
c) Giá trị nhỏ nhất của hàm số là \( - 2\).
d) Parabol cắt trục \(Ox\) tại hai điểm \(A,\;B\). Khi đó diện tích tam giác \(IAB\) bằng \(1\).
Một cầu thủ bóng chuyền đón bóng bước 1, quả bóng nảy lên và chuyển động với vận tốc ban đầu
\({v_0}\left( {{\rm{m/s}}} \right)\) theo quỹ đạo là một đường parabol. Chọn hệ trục tọa độ \(Oxy\) sao cho tọa độ quả bóng ở thời điểm quả bóng bắt đầu nảy lên khỏi cánh tay của cầu thủ là \(\left( {0;{y_0}} \right)\), \({y_0}\) là độ cao của quả bóng so với mặt sân. Gọi \(\alpha \) là góc hợp bởi hướng nảy lên của quả bóng so với phương ngang thì quỹ đạo chuyển động của quả bóng có phương trình là \(y = \frac{{ - 4,9{x^2}}}{{v_0^2{{\cos }^2}\alpha }} + \tan \alpha \cdot x + {y_0}\).

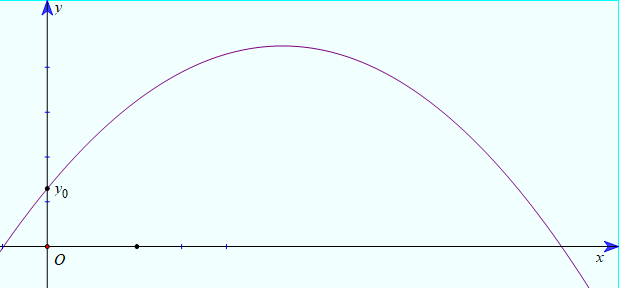
Giả sử quả bóng nảy lên với vận tốc ban đầu \({v_0} = 7\left( {{\rm{m/s}}} \right)\) ở độ cao \({y_0} = 0,8\,\left( {\rm{m}} \right)\).
a) Quỹ đạo chuyển động của quả bóng là \(y = \frac{{ - 0,1}}{{{{\cos }^2}\alpha }} \cdot {x^2} + \tan \alpha \cdot x + 0,8\).
b) Nếu \(\alpha = 30^\circ \), sau 2 giây quả bóng ở độ cao trên \(1,7\left( {\rm{m}} \right)\).
c) Nếu \(\alpha = 60^\circ \), quả bóng sẽ đạt độ cao tối đa là \(3\left( {\rm{m}} \right)\).
d) Nếu \(\alpha = 60^\circ \) và không có cầu thủ nào đón bóng bước 2 thì quả bóng sẽ chạm mặt sân cách vị trí tiếp xúc với cánh tay cầu thủ đón bóng bước 1 một khoảng là \(4,818\left( {\rm{m}} \right)\).
chữ viết tắt: lớn
Cho hàm số bậc hai \(y = a{x^2} + bx + c\;\left( P \right)\) có đồ thị như hình vẽ sau:
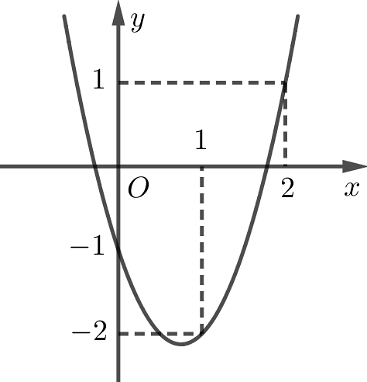
a) \(a > 0\).
b) \(c > 0\).
c) \(a - 2b + c = 9\).
d) Đường thẳng \(\left( d \right):y = x + 5\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.
Cho hàm số \(y = - {x^2} + 6x - 5\).
a) Giao điểm của đồ thị hàm số đã cho với trục tung tại điểm có tung độ bằng \( - 5\).
b) Đỉnh của đồ thị hàm số đã cho là \(I\left( {2;3} \right)\).
c) Giá trị lớn nhất của hàm số bằng \(3\).
d) Đường thẳng \(d:y = 4x - m\) cắt đồ thị hàm số đã cho tại 2 điểm phân biệt khi \(m > 4\).
Một vật chuyển động có vận tốc \(({\rm{m}}/{\rm{s}})\) được biểu diễn theo thời gian \(t(\;{\rm{s}})\) bằng công thức \(v\left( t \right) = \frac{1}{2}{t^2} - 4t + 10\). Vận tốc của vật đạt giá trị nhỏ nhất bằng bao nhiêu (đơn vi: m/s)?
Biết rằng hàm số \[y = a{x^2} + bx + c\] đạt giá trị lớn nhất bằng \[ - 4\] tại \[x = 2\] và đồ thị hàm số đi qua điểm \[A\left( {0; - 5} \right)\]. Giá trị của biểu thức \[T = a + b - c\] bằng bao nhiêu?
Cổng vòm hoa tại một lễ cưới có hình dạng là đường parabol. Biết khoảng cách giữa hai chân cổng vòm hoa là \(3,2\,{\rm{m}}\). Tại vị trí trên cổng vòm hoa có độ cao \(2\,{\rm{m}}\) so với mặt đất người ta thả một sợi dây chạm đất cách chân \(A\) của cổng vòm hoa một đoạn \(1\,{\rm{m}}\) (như hình vẽ). Tính chiều cao của cổng vòm hoa (theo đơn vị mét và làm tròn kết quả đến hàng phần trăm).
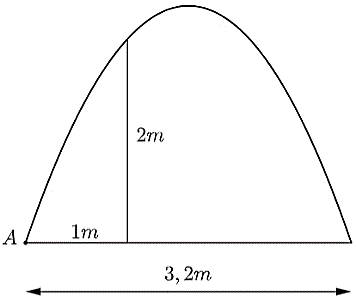
Một nhà hát có sức chứa 800 người. Với giá vé 40 nghìn đồng trung bình sẽ có 300 người đến nhà hát mỗi ngày. Để tăng doanh thu, nhà hát đã khảo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 nghìn đồng sẽ có thêm 100 người đến mỗi ngày. Gọi \(A\) nghìn đồng là giá vé để doanh thu từ tiền bán vé của nhà hát là lớn nhất. Tính giá trị của biểu thức \({A^2} + 2025\).
Một cửa hàng bán bưởi da xanh với giá bán mỗi quả là 60 000 đồng. Với giá bán này thì mỗi ngày cửa hàng chỉ bán được 30 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 1 000 đồng thì số bưởi bán tăng thêm được là 10 quả. Xác định giá bán (đơn vị: nghìn đồng) để cửa hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả là 35 000 đồng.