15 câu Trắc nghiệm Tin học 7 Chân trời sáng tạo Bài 2 có đáp án (Phần 2)
15 câu hỏi
Hệ điều hành không có nhiệm vụ gì trong các nhiệm vụ dưới đây?
Quản lí toàn bộ hoạt động của máy tính.
Điều khiển toàn bộ hoạt động của máy tính.
Cầu nối trung gian trao đổi thông tin giữa người dùng với máy tính.
Giúp người dùng sử dụng máy tính không cần thao tác.
Hệ điều hành không có chức năng nào dưới đây?
Quản lí, điều khiển các thiết bị phần cứng hoạt động nhịp nhàng, hiệu quả.
Quản lí, điều khiển các tiến trình (các phần mềm đang chạy trên máy tính), cấp phát, thu hồi tài nguyên (như CPU, bộ nhớ, …) phục vụ các tiến trình.
Quản lí tài khoản người dùng, cung cấp môi trường trao đổi thông tin giữa người sử dụng và máy tính.
Tổ chức quản lí người sử dụng máy tính.
Chọn khẳng định sai trong các khẳng định sau?
Phần mềm ứng dụng là những chương trình máy tính, cung cấp công cụ hỗ trợ con người xử lí công việc trên máy tính.
Chương trình máy tính là dữ liệu được lưu trữ trên ổ đĩa dưới dạng tệp, khi người dùng khởi động phần mềm ứng dụng, hệ điều hành sẽ điều khiển tải dữ liệu này vào bộ nhớ trong và tổ chức thực hiện chương trình.
Phần mềm ứng dụng tương tác với thiết bị phần cứng thông qua người dùng.
Hệ điều hành kết nối, quản lí, điều khiển các thiết bị phần cứng, phần mềm trên máy tính, đảm bảo chúng phối hợp, hoạt động nhịp nhàng trong một hệ thống nhất.
Hệ điều hành là chương trình hoạt động giữa người sử dụng với:
Phần mềm của máy tính.
Phần cứng của máy tính.
Các chương trình ứng dụng.
CPU và bộ nhớ.
Hệ điều hành là gì?
Một phần mềm công cụ.
Một phần mềm hệ thống.
Một phần mềm ứng dụng.
Một phần mềm tiện ích.
Phần mềm trình chiếu (Microsoft Power Point) là:
Phần mềm hệ thống.
Phần mềm công cụ.
Phần mềm tiện ích.
Phần mềm ứng dụng.
Có mấy loại phần mềm máy tính?
1.
2.
3.
4.
Có mấy loại phần mềm ứng dụng:
2.
3.
4.
5.
Trong máy tính phần mềm nào là quan trọng nhất?
Phần mềm hệ thống.
Phần mềm ứng dụng.
Phần mềm tiện ích.
Phần mềm công cụ.
Hình ảnh dưới đây thể hiện chức năng gì của hệ điều hành?
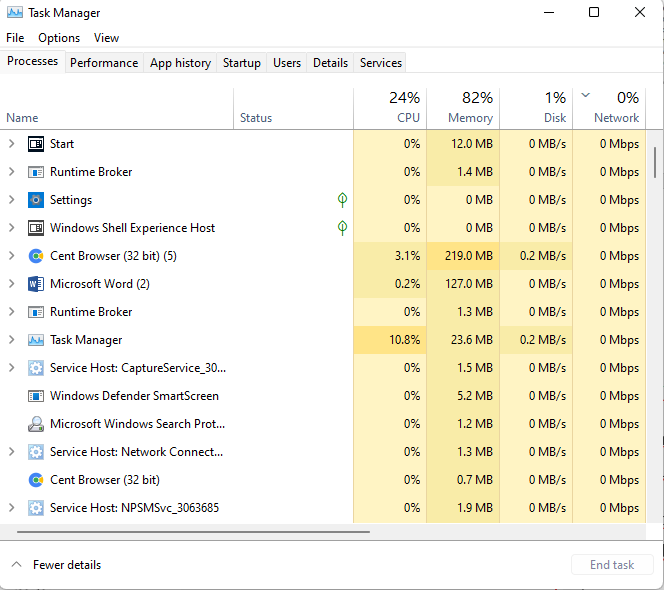
Quản lí, điều khiển các tiến trình (các phần mềm đang chạy trên máy tính), cấp phát, thu hồi tài nguyên (như CPU, bộ nhớ, …) phục vụ các tiến trình.
Quản lí tài khoản người dùng, cung cấp môi trường trao đổi thông tin giữa người sử dụng và máy tính.
Tổ chức quản lí, lưu trữ dữ liệu trong máy tính.
Quản lí, điều khiển các thiết bị phần cứng hoạt động nhịp nhàng, hiệu quả.
Đâu không phải hệ điều hành dành cho máy tính?
Windowns.
Linux.
MacOs.
iOS.
Hệ điều hành được lưu trữ ở đâu?
Bộ nhớ trong (Rom, Ram).
Bộ nhớ ngoài (Đĩa cứng, CD, ...).
Bộ xử lý trung tâm.
Kết quả khác.
Hệ điều hành nào mà các chương trình phải được thực hiện lần lượt và chỉ 1 người được đăng nhập vào hệ thống?
Đa nhiệm 1 người dùng.
Đơn nhiệm 1 người dùng.
Đa nhiệm nhiều người dùng.
Kết quả khác.
Tìm câu sai trong các câu dưới đây khi nói về hệ điều hành:
Hệ điều hành đảm bảo giao tiếp giữa người dùng và máy tính.
Chức năng chính của hệ điều hành là thực hiện tìm kiếm thông tin trên Internet.
Hệ điều hành cung cấp các phương tiện và dịch vụ để người sử dụng dễ dàng thực hiện chương trình, quản lí chặt chẽ, khai thác các tài nguyên của máy tính một cách tối ưu.
Hệ điều hành Windows là hệ điều hành dùng cho máy tính cá nhân của hãng Microsoft.
Chọn phát biểu không đúng?
Phần mềm ứng dụng tương tác với thiết bị phần cứng thông qua hệ điều hành.
Phần mềm ứng dụng chạy trên nền của hệ điều hành, là công cụ, tiện ích cho phép người dùng xử lí các công việc cụ thể trên máy tính.
Phần mềm ứng dụng là những chương trình máy tính, cung cấp công cụ hỗ trợ con người xử lí công việc trên máy tính.
Khi ngoài dùng khởi động phần mềm ứng dụng, hệ điều hành sẽ điều khiển tải dữ liệu này vào bộ nhớ ngoài và tổ chức thực hiện chương trình.

