20 câu trắc nghiệm Toán 8 Kết nối tri thức: Ôn tập chương II (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn, yêu cầu chọn phương án đúng nhất)
Phân tích đa thức \(27{y^3} + 9{y^2} + y + \frac{1}{{27}}\) thành nhân tử ta được
\({\left( {3y + \frac{1}{3}} \right)^3}.\)
\({\left( {3y - \frac{1}{3}} \right)^3}.\)
\({\left( {\frac{1}{3} - 3y} \right)^3}.\)
\({\left( { - \frac{1}{3} - 3y} \right)^3}.\)
Tích \(\left( {2x - 3} \right)\left( {2x + 3} \right)\) có kết quả bằng
\(4{x^2} - 9.\)
\(2{x^2} - 3.\)
\(4{x^2} + 9.\)
\(4{x^2} + 12x + 9.\)
Điền vào chỗ trống: \({\left( {\frac{1}{2}x - y} \right)^2} = \frac{1}{4}{x^2} - ...... + {y^2}\).
\(2xy.\)
\(xy.\)
\( - 2xy.\)
\(\frac{1}{2}xy.\)
Rút gọn biểu thức \({\left( {a + b} \right)^2} - {\left( {a - b} \right)^2}\) được kết quả là
\(4ab.\)
\( - 4ab.\)
\(0.\)
\(2{b^2}.\)
Chọn khẳng định đúng.
\(\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = {x^3} - 1\).
\(\left( {x - 1} \right)\left( {x + 1} \right) = 1 - {x^2}.\)
\(\left( {x - 1} \right)\left( {x + 1} \right) = {x^2} + 1.\)
\(\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = 1 - {x^2}.\)
Đẳng thức đúng là
\(27 + 27x + 9{x^2} + {x^3} = {\left( {3 + x} \right)^3}.\)
\({x^3} - 3{x^2} + 3x - 1 = {\left( {1 - x} \right)^3}.\)
\(1 - 2y + {y^2} = - {\left( {y - 1} \right)^2}.\)
\(1 - {x^2}{y^4} = - \left( {1 - x{y^2}} \right)\left( {1 + x{y^2}} \right)\).
Rút gọn biểu thức \(Q = \left( {{x^2} + xy + {y^2}} \right)\left( {x - y} \right) + \left( {{x^2} - xy + {y^2}} \right)\left( {x + y} \right)\) là
\(0.\)
\(2{y^3}\).
\(2xy.\)
\(2{x^3}.\)
Đẳng thức nào sau đây là sai?
\({\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} = 4ab.\)
\({\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right)\).
\({\left( { - a - b} \right)^2} = - {\left( {a + b} \right)^2}.\)
\(\left( { - a - b} \right)\left( { - a + b} \right) = {a^2} - {b^2}.\)
Phân tích đa thức \({a^3} - {a^2}x - a{y^2} + x{y^2}\) thành nhân tử ta được
\(\left( {a - x} \right)\left( {y - a} \right)\left( {a + y} \right).\)
\(\left( {a - x} \right)\left( {a - y} \right)\left( {a + y} \right).\)
\(\left( {x - a} \right)\left( {a - y} \right)\left( {a + y} \right).\)
\(\left( {a - x} \right)\left( {a - y} \right)\left( {a + y} \right).\)
Trong các biểu thức sau, biểu thức nào luôn nhận giá trị dương:
\(A = {x^2} - x - 6.\)
\(B = {x^2} + x - 2.\)
\(C = {x^2} - x + 1.\)
\(D = {x^2} + 6x - 1.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, mỗi câu hỏi có 4 ý khẳng định, yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định)
Cho biểu thức \(C = - {x^2} - {y^2} + 4x - 4y + 2\)
a) \(C = 10 - {\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2}\).
b) Không có giá trị nào của \(x,y\) để \(C = 0\).
c) Giá trị nhỏ nhất của \(C = 10\).
d) Biểu thức \(C\) đạt giá trị lớn nhất khi \(x = 2,y = - 2.\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như hình vẽ dưới đây.
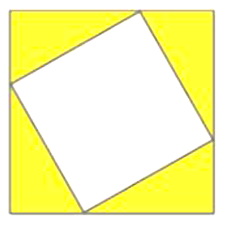
Trong đó, ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là 168 cm và diện tích phần không gắn ảnh (phần tô màu) là 252 cm2. Gọi \(x,y\) lần lượt là độ dài cạnh của hình vuông nhỏ và lớn \(\left( {x,y > 0,{\rm{ cm}}} \right)\).
a)Tổng chiều dài các thành kim loại làm khung là 168 cm nên \(4x + 4y = 168\).
b)Đa thức biểu diễn phần diện tích không gắn ảnh là \(S = {x^2} - {y^2}\).
c)Độ dài cạnh của hình vuông lớn là \(18\) cm.
d)Diện tích phần được gắn ảnh lớn hơn 300 cm2.
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Một thử ruộng hình chữ nhật có chiều dài bằng \(20{\rm{ m}}\), chiều rộng bằng \(\frac{1}{2}\) chiều dài. Nếu giảm chiều dài đi \(x{\rm{ }}\left( {\rm{m}} \right)\) và tăng chiều rộng thêm \(x{\rm{ }}\left( {\rm{m}} \right)\).
a)Chiều rộng ban đầu của thửa ruộng là \(10{\rm{ }}\left( {\rm{m}} \right)\).
b)Diện tích của thửa ruộng sau khi thay đổi chiều dài, chiều rộng là \(\left( {20 - x} \right)\left( {10 + x} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c)Sau khi giảm chiều dài đi \(x{\rm{ }}\left( {\rm{m}} \right)\) và tăng chiều rộng thêm \(x{\rm{ }}\left( {\rm{m}} \right)\) thì diện tích thửa ruộng không thể vượt quá \(225{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
d)Diện tích thửa ruộng sau khi thay đổi đạt giá trị lớn nhất khi \(x = 2{\rm{ }}\left( {\rm{m}} \right).\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Từ một sợi dây có dộ dài \(200{\rm{ cm}}{\rm{,}}\) Hùng cắt ra thành hai đoạn dây, một đoạn lớn, một đoạn nhỏ, mỗi đoạn có độ dài theo centimet là một số tự nhiên chia hết cho 4. Hùng đặt hai đoạn dât trên mặt bàn sao cho mỗi đoạn dây tạo thành một hình cuông, hình vuông nhỏ nằm trong hình vuông lớn. Gọi độ dài đoạn dây lớn và nhỏ lần lượt được cắt ra là \(4x\) và \(4y\) \(\left( {x,y \in {\mathbb{N}^*},{\rm{ cm}}} \right)\).
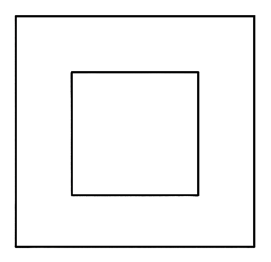
a) Tổng độ dài hai cạnh hình vuông lớn và hình vuông nhỏ là 50 cm.
b) Diện tích phần nằm giữa hai hình vuông là \(S = 50\left( {x - y} \right){\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
c) Để diện tích phần nằm giữa hai hình vuông lớn nhất thì cạnh hình vuông lớn có độ dài là 49 cm, cạnh hình vuông nhỏ có độ dài là 1 cm.
d) Để diện tích phần nằm giữa hai hình vuông lớn nhất thì cắt sợi dây có độ dài thành hai đoạn 196 cm và 4 cm.
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Một thùng chứa dạng hình lập phương có độ dài cạnh bằng \(x\) (cm). Phần vỏ bao gồm nắp có độ dày 3 cm.
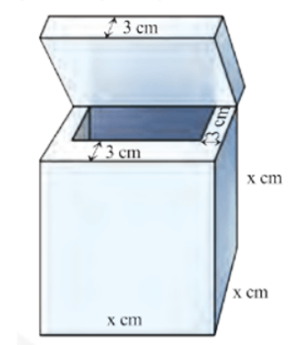
a)Phần lòng trong của thùng có độ dài cạnh là \(x - 6\) (cm).
b)Thể tích của thùng là \({x^3}\) (cm3).
c)Thể tích phần dung tích của thùng là \({\left( {x - 6} \right)^3}\) cm3.
d)Thể tích phần vỏ của thùng là \(18{x^2} + 108x + 216\) cm3.
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, mỗi câu hỏi yêu cầu đưa ra đáp án là một con số, tối đa có 4 kí tự, tính cả kí tự dấu và kí tự dấu phẩy
Cho các số thực \(x;y\) thỏa mãn điều kiện \(x + y = 4;{\rm{ }}{x^2} + {y^2} = 20\). Tính giá trị của biểu thức \({x^3} + {y^3}\).
Cho \(x + y = 1.\) Tìm giá trị nhỏ nhất của biểu thức \(A = {x^3} + {y^3} + xy\). (Kết quả ghi dưới dạng số thập phân)
Tìm giá trị của \(x,\) biết: \({\left( {3x + 4} \right)^2} - \left( {3x - 1} \right)\left( {3x + 1} \right) = 65.\)
Biết \(x + y = 15\) và \(xy = - 100\). Tính giá trị của biểu thức \(B = {x^2} + {y^2}.\)
Có bao nhiêu cặp số \(\left( {x;y} \right)\) thỏa mãn \(3{x^2} + {y^2} + 10x - 2xy + 29 = 0\)?
