20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn, yêu cầu chọn phương án đúng nhất)
Có bao nhiêu đa thức trong các biểu thức dưới đây sau:
\(2025;{\rm{ }}{x^2} + 2{y^2};{\rm{ }}\frac{1}{x} + 3y;{\rm{ }}\frac{x}{3} + 3xy;{\rm{ }}\sqrt z + 2y\)
2.
3.
4.
5.
Cho đa thức \(P\left( x \right) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}\). Thu gọn và sắp xếp đa thức \(P\left( x \right)\) theo lũy thừa giảm dần của biến, ta được
\(P\left( x \right) = 3 + 2x + 9{x^2}.\)
\(P\left( x \right) = 5{x^5} - 4{x^3} + 9{x^2} - 2x + 3.\)
\(P\left( x \right) = 3{x^5} - 4{x^3} + 9{x^2}.\)
\(P\left( x \right) = 2x + 9.\)
Bậc của đa thức \(3{x^2}{y^3} - xy - 2{x^2}{y^3} + xy + 1\) là
3.
0.
1.
5.
Kết quả của phép tính \(3xy.4{x^2}y\) là
\(12{x^3}{y^2}.\)
\(12{x^2}{y^2}.\)
\(12{x^2}{y^3}.\)
\(12{x^3}{y^3}.\)
Một mảnh đất hình chữ nhật có chiểu rộng là \(x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài hơn chiều rộng \(4{\rm{ }}\left( {\rm{m}} \right)\). Đa thức biểu thị diện tích của hình chữ nhật đó là
\(2x + 4{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\({x^2} + 4x{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\({x^2} - 4x{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(2{x^2} + 4{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Khẳng định đúng là
\(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = 4{x^2} - 25{y^2}.\)
\(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = 2{x^2} - 5{y^2}.\)
\(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = 4{x^2} + 25{y^2}.\)
\(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = 4{x^2} + 5{y^2}.\)
Đơn thức \(10{x^3}{y^2}{z^3}\) chia hết cho đơn thức nào?
\(5{x^3}{y^2}{z^2}\).
\( - 2{x^4}{y^2}z.\)
\( - 9{x^3}y{z^2}.\)
\(2{x^3}{y^3}{z^3}.\)
Kết quả của phép chia \(6{x^3} + 4{x^2} - 2x\) cho đơn thức \(\left( { - 2x} \right)\) là
\( - 3{x^3} - 2x + 1.\)
\( - 3{x^3} + 2x + 1.\)
\( - 3{x^2} - 2x + 1.\)
\( - 3{x^3} - 2x - 1.\)
Đa thức \(N\) thỏa mãn \(N - \left( {xy - 2{y^2}} \right) = 4xy + {x^2} - 9{y^2}\) là
\(N = 3xy + {x^2} - 11{y^2}\).
\(N = 5xy + {x^2} + 7{y^2}.\)
\(N = 3xy + {x^2} + 7{y^2}.\)
\(N = 5xy + {x^2} - 11{y^2}\).
Kết quả của phép chia \(\left( {20{x^3} - 15{x^2} + 5x} \right):5x\) bằng
\(4{x^2} - 3x + 1.\)
\(4{x^2} + 3x + 1.\)
\(5{x^2} - 3x + 1.\)
\(4{x^3} - 3{x^2} + x.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, mỗi câu hỏi có 4 ý khẳng định, yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định)
Cho đa thức \(A = \frac{1}{3}{x^2}y + x{y^2} - xy + \frac{1}{2}x{y^2} - 5xy - \frac{1}{3}{x^2}y\).
a)Thu gọn được \(A = \frac{3}{2}x{y^2} - 6xy\).
b)Đa thức \(A\) có bậc là 3.
c)Giá trị của \(A\) tại \(x = 2;y = - 1\) là 9.
d)Đa thức \(B = A + 6xy - 1,5x{y^2}\) có giá trị không phụ thuộc vào biến \(x;y.\)
Cho biểu thức \(Q = \left( {2n - 1} \right)\left( {2n + 3} \right) - \left( {4n - 5} \right)\left( {n + 1} \right) + 3\).
a) Thu gọn được \(Q = 5n - 5\).
b) Bậc của đa thức \(Q\) là 5.
c) Giá trị của \(Q = 0\) khi \(x = \frac{1}{5}\).
d) Biểu thức \(Q\) luôn chia hết cho 5 với mọi \(n \in \mathbb{Z}.\)
Một tấm bìa cứng hình chữ nhật có chiều dài \(x + 43{\rm{ }}\left( {{\rm{cm}}} \right),\) chiều rộng là \(x + 30{\rm{ }}\left( {{\rm{cm}}} \right).\) Người ta cắt ở mỗi góc của tấm bìa một hình vuông cạnh \({y^2}{\rm{ + 1 }}\left( {{\rm{cm}}} \right)\) (phần tô màu) và xếp phần còn lại thành một cái hộp không nắp.
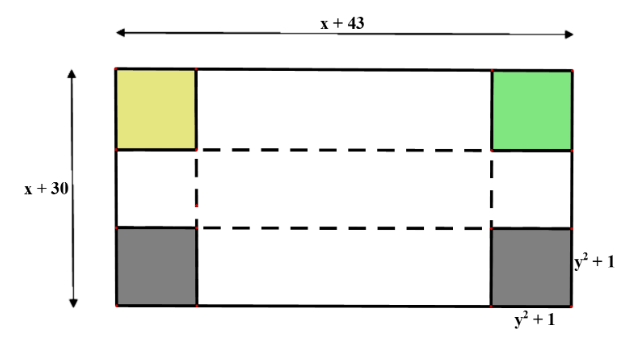
a) Chiều dài của hình hộp chữ nhật là \(x - 2{y^2} + 41{\rm{ }}\left( {{\rm{cm}}} \right)\).
b) Chiều rộng của hình hộp chữ nhật là \(x - 2{y^2} + 28{\rm{ }}\left( {{\rm{cm}}} \right).\)
c) Biểu thức biểu thị diện tích xung quanh của hình hộp chữ nhật là
\(S = 4x{y^2} - 8{y^4} + 130{y^2} + 4x + 138{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
d) Diện tích xung quanh hình hộp chữ nhật có giá trị lớn hơn \({\rm{1250 }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\) khi \(x = 16;y = 4.\)
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng một hình vuông, biết chu vi hình vuông là \(20{\rm{ }}\left( {\rm{m}} \right)\) sau đó được mở rộng bên phải thêm \(y{\rm{ }}\left( {\rm{m}} \right),\) phía dưới thêm \(8x{\rm{ }}\left( {\rm{m}} \right)\) nên mảnh vườn trở thành một hình chữ nhật (hình minh họa bên dưới).
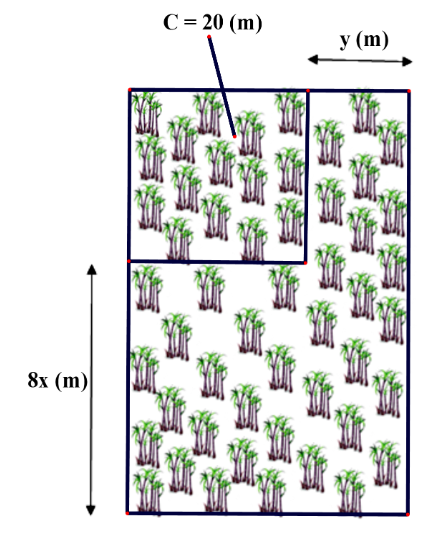
a) Chiều rộng của khu vườn sau khi được mở rộng là \(y + 5{\rm{ }}\left( {\rm{m}} \right)\).
b) Chiều dài của khu vườn sau khi được mở rộng là \(8x + 5{\rm{ }}\left( {\rm{m}} \right)\).
c) Biểu thức biểu diễn diện tích của khu vườn sau khi mở rộng là \(8xy + 5y + 40x + 25{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
d) Diện tích của mảnh vườn sau khi được mở rộng có diện tích lớn hơn \(90{\rm{ }}\left( {{{\rm{m}}^2}} \right)\) khi
\(x = 1;y = 2.\)
Bác Nam có một mảnh vườn hình chữ nhật. Bác chia mảnh vườn này ra làm hai khu đất hình chữ nhật: Khu thứ nhất dùng để trồng có. Khu thứ hai dùng để trồng hoa (Với các kích thước như hình vẽ)
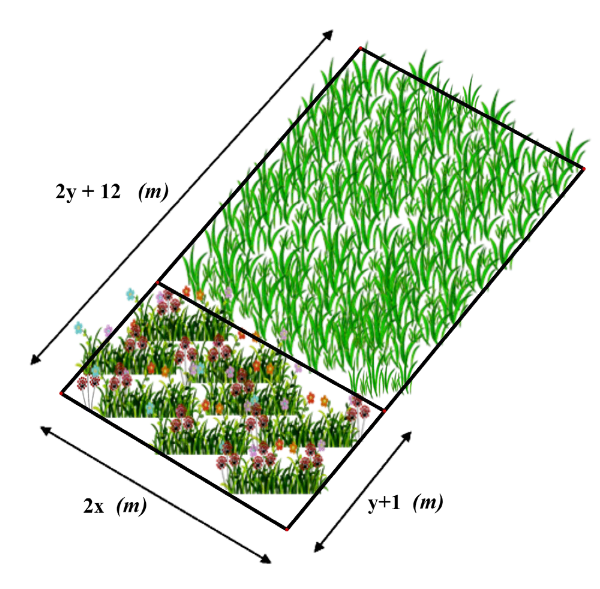
a) Diện tích của khu đất dùng để trồng hoa là \({S_1} = 2xy + 2x{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\)
b) Chiều dài của khu đất dùng để trồng cỏ là \(y - 11{\rm{ }}\left( {\rm{m}} \right)\).
c) Diện tích khu đất dùng để trồng cỏ là \({S_2} = 2xy - 22x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Diện tích của cả mảnh vườn lớn hơn \(150{\rm{ }}{{\rm{m}}^2}\) khi \(x = 4;y = 4.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, mỗi câu hỏi yêu cầu đưa ra đáp án là một con số, tối đa có 4 kí tự, tính cả kí tự dấu và kí tự dấu phẩy
Tính giá trị của biểu thức \(C = \left( {{a^2} - 2} \right)\left( {{a^2} + a - 1} \right) - \left( {{a^2} + a} \right)\left( {{a^2} - 3} \right) - a + 10\).
Tính giá trị của biểu thức \(A = \left( {2x - y} \right)\left( {2x + y} \right) - \left( {4{x^2} + 2{y^2}} \right)\) tại \(x = 999;y = 1.\)
Cho ba số tự nhiên liên tiếp. Tích của hai số đầu nhỏ hơn tích của hai số sau là 50. Hỏi số nhỏ nhất có giá trị bằng bao nhiêu?
Tìm giá trị của \(x,\) biết: \(3\left( {x - 7} \right)\left( {x - 5} \right) - \left( {x - 1} \right)\left( {3x + 2} \right) = 2\).
Cho \(a,b,c\) là các số thực thỏa mãn \(ab + bc + ac = abc\) và \(a + b + c = 1\). Tính giá trị của biểu thức \(A = \left( {a - 1} \right)\left( {b - 1} \right)\left( {c - 1} \right)\).
