20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 33. Hai tam giác đồng dạng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Nếu \(\Delta ABC \sim \Delta A'B'C'\)theo tỉ số đồng dạng 2 thì \(\Delta A'B'C' \sim \Delta ABC\)theo tỉ số đồng dạng
1
2
\(\frac{1}{2}.\)
\(\sqrt 2 .\)
Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}};\;\,\widehat {A'} = \widehat A;\;\,\widehat {B'} = \widehat B;\;\,\widehat {C'} = \widehat C\) thì
\(\Delta A'B'C' = \Delta ABC.\)
\(\Delta A'B'C' \sim \Delta ABC.\)
\(\Delta A'C'B' = \Delta ABC.\)
\(\Delta A'C'B' \sim \Delta ABC.\)
Nếu \(\Delta ABC \sim \Delta MNP\) thì
\(\widehat A = \widehat M.\)
\(\widehat A = \widehat N.\)
\(\widehat A < \widehat M.\)
\(\widehat A > \widehat M.\)
Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng bằng
1
2.
\(\frac{1}{2}.\)
3.
Nếu \(\Delta A''B''C'' \sim \Delta A'B'C'\)theo tỉ số đồng dạng 2 và \(\Delta A'B'C' \sim \Delta ABC\)theo tỉ số đồng dạng 3 thì \(\Delta A''B''C'' \sim \Delta ABC\)theo tỉ số đồng dạng là
1
\(\frac{2}{3}.\)
\(\frac{3}{2}.\)
6.
Biết rằng \(\Delta ABC \sim \Delta HIK,\) khẳng định nào sau đây không đúng?
\(\Delta ACB \sim \Delta HKI.\)
\(\Delta BCA \sim \Delta IKH.\)
\(\Delta CBA \sim \Delta KHI.\)
\(\Delta BAC \sim \Delta IHK.\)
Cho \(\Delta ABC,\) một đường thẳng bất kì song song với \(BC\) cắt hai cạnh \(AB;\;\,AC\) lần lượt tại \(M\) và \(N.\) Khi đó:
\(\Delta AMN \sim \Delta ACB.\)
\(\Delta AMN \sim \Delta ABC.\)
\(\Delta AMN \sim \Delta BCA.\)
\(\Delta AMN \sim \Delta CBA.\)
Biết rằng \(\Delta ABC \sim \Delta A'B'C'\)và \(AB = 2A'B'.\) Khi đó:
\(\frac{{BC}}{{B'C'}} < 2.\)
\(\frac{{BC}}{{B'C'}} < \frac{1}{2}.\)
\(\frac{{BC}}{{B'C'}} = \frac{1}{2}.\)
\(\frac{{BC}}{{B'C'}} = 2.\)
Biết rằng \(\Delta ABC \sim \Delta HIK\) và \(\widehat B = 60^\circ ,\) khi đó:
\(\widehat I = 50^\circ .\)
\(\widehat I = 60^\circ .\)
\(\widehat I = 70^\circ .\)
\(\widehat I = 30^\circ .\)
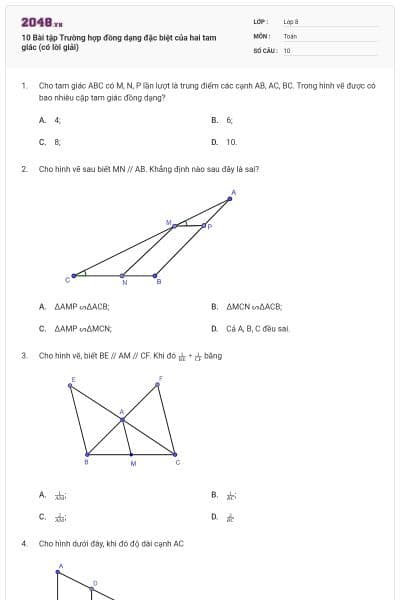
Cho \(\Delta ABC \sim \Delta MNP;\;\,\frac{{BC}}{{AC}} = 2;\;\,MP = 8\;{\rm{cm}}{\rm{.}}\)
Độ dài cạnh \(NP\) bằng
\(12\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
\(16\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
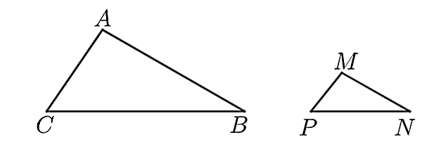
Cho hình vẽ:
Biết rằng chu vi \(\Delta ABC\) bằng \(40\;\,{\rm{cm}}{\rm{.}}\) Khi đó:
\(MN\;{\rm{//}}\;BC.\)
\(\Delta AMN \sim \Delta ACB.\)
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{5}{8}.\)
Chu vi \(\Delta MNP\) bằng \(30\;{\rm{cm}}{\rm{.}}\)
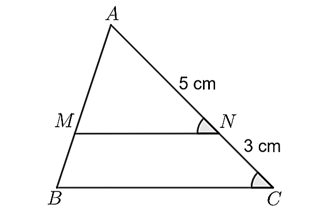
Cho hình vẽ:
Biết rằng \(\Delta ABC \sim \Delta MNP.\) Khi đó:
\(\Delta MNP\) vuông tại \(M.\)
Diện tích \(\Delta MNP\) là \({S_{MNP}} = \frac{1}{4} \cdot PM \cdot MN.\)
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{PM}} = 4.\)
Diện tích \(\Delta ABC\) gấp 4 lần diện tích \(\Delta MNP.\)
Cho hình vẽ sau:
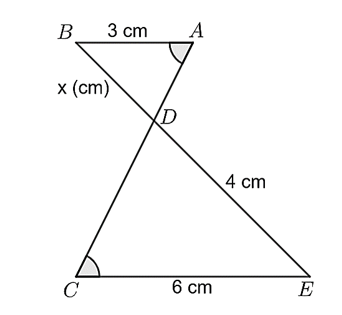
Khi đó:
\(AB\;{\rm{//}}\;CE.\)
\(\Delta DAB \sim \Delta DCE.\)
\(\Delta DAB\) đồng dạng với \(\Delta DCE\) theo tỷ số đồng dạng bằng \(\frac{1}{2}.\)
\(x > 3\;\,{\rm{cm}}{\rm{.}}\)
Cho hình bình hành \(ABCD\) có \(E,\;\,F\) lần lượt là trung điểm của \(DC,\;\,AC.\)
\(EF\;{\rm{//}}\;AD.\)
\(\Delta CEF\) đồng dạng với \(\Delta CAD\) theo tỉ số đồng dạng \(\frac{2}{3}.\)
\(\Delta CAD = \Delta ACB.\)
\(\Delta CEF\) đồng dạng với \(\Delta ACB\) theo tỉ số đồng dạng \(\frac{1}{2}.\)
Cho tam giác \(ABC\) có \(AB = 12\;\,{\rm{cm; }}AC = 18\;\,{\rm{cm}}{\rm{.}}\) Lấy các điểm \(M,\;N\) lần lượt trên các cạnh \(AB,\;\,AC\) sao cho \(AM = 8\;\,{\rm{cm; }}AN = 12\;\,{\rm{cm}}{\rm{.}}\) Lấy điểm \(P\) trên cạnh \(AC\) sao cho \(AP = 8\;\,{\rm{cm}}{\rm{.}}\)
\(MN\) không song song với \(BC.\)
\(\Delta AMN \sim \Delta ABC.\)
\(\Delta APB = \Delta AMN.\)
\(\Delta APB \sim \Delta ACB.\)
Cho tam giác \(ABC.\) Gọi \(M,\;\,N\) lần lượt là trung điểm của \(AB,\;\,AC.\) Tam giác \(ABC\) đồng dạng với tam giác \(AMN\) theo tỉ số đồng dạng là bao nhiêu?
Cho \(\Delta ABC\) đồng dạng với \(\Delta DEF\) và \(\widehat A = 40^\circ ;\;\,\widehat F = 70^\circ .\) Hỏi số đo \(\widehat E\) bằng bao nhiêu độ?
Cho \(\Delta ABC \sim \Delta MNP.\) Biết rằng \(\widehat B + \widehat C = 90^\circ .\) Hỏi số đo góc \(M\) bằng bao nhiêu độ?
Biết rằng \(\Delta ABC \sim \Delta HIK,\;\,\widehat A = 90^\circ ,\;\,AB = 2HI.\) Hỏi diện tích \(\Delta ABC\) gấp bao nhiêu lần diện tích \(\Delta HIK?\)
Cho \(\Delta ABC \sim \Delta MNP\) và \(\frac{{\widehat A}}{1} = \frac{{\widehat B}}{2} = \frac{{\widehat C}}{3}.\) Hỏi số đo góc \(M\) của \(\Delta MNP\) bằng bao nhiêu độ?