20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Đồ thị của hàm số bậc nhất là
Đoạn thẳng.
Tia.
Đường gấp khúc.
Đường thẳng.
Hàm số \(y = ax + b\) là hàm số bậc nhất khi
\(a = 0.\)
\(b = 0.\)
\(a \ne 0.\)
\(b \ne 0.\)
Hàm số nào dưới đây là hàm số bậc nhất?
\(y = 1 - x.\)
\(y = {x^2} - 1.\)
\(y = \sqrt x .\)
\(y = 0x + 1.\)
Cho các hình vẽ sau:
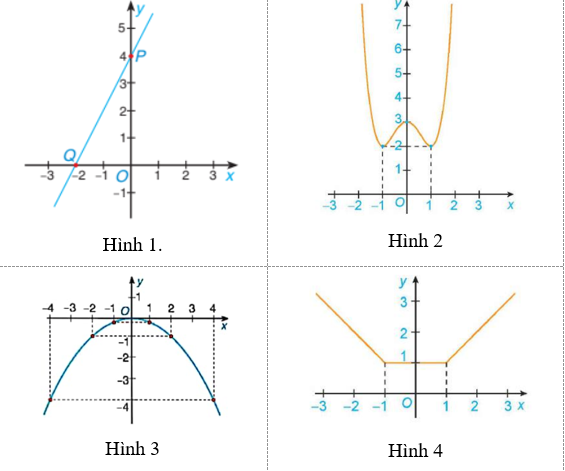
Hình vẽ nào thể hiện đồ thị hàm của số bậc nhất?
Hình 4.
Hình 3.
Hình 2
Hình 1.
Hàm số bậc nhất nào dưới đây có hệ số tự do bằng 2?
\(y = x - \left( { - 2} \right).\)
\(y = - 2 - x.\)
\(y = 2x + 1.\)
\(y = 2x - 2.\)
Cho hàm số bậc nhất \(y = 2x + 7,\) với \(x = - 1\) thì
\(y = - 5.\)
\(y = 5.\)
\(y = - 9.\)
\(y = 9.\)
Đồ thị hàm số bậc nhất \(y = ax\left( {a \ne 0} \right)\) luôn đi qua điểm
\(A\left( {0;\;\,1} \right).\)
\(B\left( {0;\; - 1} \right).\)
\(O\left( {0;\;\,0} \right).\)
\(D\left( {1;\;\,1} \right).\)
Với giá trị nào của \(m\) thì hàm số \(y = \left( {m - 10} \right)x + 6\) là hàm số bậc nhất?
\(m > 10.\)
\(m < 10.\)
\(m \ne 10.\)
\(m \ge 10.\)
Điểm nào dưới đây thuộc đồ thị của hàm số bậc nhất \(y = - 6x + 5?\)
\(A\left( {0;\;\,1} \right).\)
\(B\left( {0;\;\,5} \right).\)
\(C\left( {0;\;\,3} \right).\)
\(D\left( {0;\;\,4} \right).\)
Biết rằng đồ thị của hàm số bậc nhất \(y = 3x + b\) đi qua điểm \(A\left( {1;\;\,6} \right),\) khi đó:
\(b = 1.\)
\(b = 2.\)
\(b = 3.\)
\(b = 4.\)
Cho hàm số bậc nhất \(y = ax + b.\) Biết rằng đồ thị hàm số đó đi qua 2 điểm \(A\left( {0;\;\,1} \right)\) và \(B\left( {2;\;\,5} \right).\)
Hàm số đã cho là hàm số bậc nhất khi \(a \ne 1.\)
\(b = 1.\)
Đồ thị hàm số đã cho là \(y = - 2x + 1.\)
Đồ thị hàm số đã cho đi qua điểm \(C\left( { - 1;\;\,3} \right).\)
Hình vẽ dưới đây là đồ thị của hàm số \(y = f\left( x \right):\)
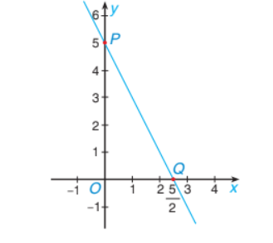
Khi đó:
Đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất.
Đồ thị hàm số \(y = f\left( x \right)\) đi qua hai điểm \(P\left( {0;\;\,\frac{5}{2}} \right)\) và \(Q\left( {5;\;\,0} \right).\)
Đồ thị hàm số trên là \(y = f\left( x \right) = - 2x + 5.\)
Điểm \(M\) có hoành độ bằng 1 thuộc đồ thị hàm số \(y = f\left( x \right)\) thì tung độ bằng 6.
Bạn An mang theo 255 nghìn đồng và đạp xe đi nhà sách để mua vở. Biết giá mỗi quyển vở là 9 nghìn đồng và phí gửi xe đạp là 3 nghìn đồng. Gọi \(y\) (nghìn đồng) là tổng số tiền bạn An cần trả cho việc gửi xe đạp và mua \(x\) quyển vở. Khi đó:
\(y = 3 + 9x\) (nghìn đồng).
\(y\) là hàm số bậc nhất của \(x.\)
Bạn An mua 20 quyển vở và trả phí gửi xe hết 190 nghìn đồng.
Với số tiền bạn An mang đi, bạn mua được nhiều hơn 25 quyển vở.
Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là \(25\;\,000\) đồng/ tháng và cước gọi là 900 đồng/ phút. Gọi \(y\) (đồng) là số tiền phải trả trong tháng khi gọi \(x\) phút.
\(y = 25\;\,000 + 900x\) (đồng).
\(y\) không là hàm số bậc nhất của \(x.\)
Số tiền phải trả khi gọi 50 phút trong một tháng là \(70\;\,000\) đồng.
Với \(200\;\,000\) đồng thì thuê bao đó gọi được nhiều hơn 200 phút một tháng.
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 30 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,5\) triệu đồng. Gọi \(y\) (triệu đồng) là chi phí để sản xuất \(x\) xe đạp trong một ngày.
\(y = 30 + 1,5{x^2}\) (triệu đồng).
\(y\) là hàm số bậc nhất của \(x.\)
Chi phí sản xuất 10 chiếc xe trong một ngày lớn hơn 50 triệu đồng.
Với chi phí trong một ngày là 220 triệu đồng thì có thể sản xuất được nhiều hơn 100 xe.
Cho hàm số bậc nhất \(y = 2 - ax.\) Tìm hệ số \(a,\) biết rằng khi \(x = 10\) thì \(y = 4.\)
Giá tiền \(y\) (đồng) khi mua \(x\;\,\left( {{\rm{kg}}} \right)\) vải thiều được cho bởi hàm số bậc nhất \(y = 40\;\,000x\) (đồng). Với số tiền \(240\;\,000\) đồng thì mua được bao nhiêu \({\rm{kg}}\) vải thiều?
Tìm giá trị của \(m\) để đồ thị hàm số bậc nhất \(y = \left( {m - 1} \right)x - 3m\) đi qua điểm \(N\left( {1;\;\,4} \right).\)
Cho đồ thị hàm số bậc nhất \(\left( d \right):\;\,y = ax\) đi qua điểm \(A\left( {4;\;8} \right).\) Tìm tung độ của điểm thuộc đồ thị hàm số \(\left( d \right)\) có hoành độ bằng \( - 2.\)
Cho hai đường thẳng \(\left( {{d_1}} \right):y = - x\) và \(\left( {{d_2}} \right):y = x + m\) có điểm \(A\left( { - 2;\;\,b} \right)\) thuộc đường thẳng \(\left( {{d_1}} \right).\) Tìm \(m\) để điểm \(A\left( { - 2;\;\,b} \right)\) cũng thuộc đường thẳng \(\left( {{d_2}} \right).\)


