20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 17. Tính chất đường phân giác của tam giác (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Cho tam giác \(ABC\) có \(AD\;\left( {D \in BC} \right)\) là đường phân giác của tam giác đó. Khi đó:
\(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}.\)
\(\frac{{AB}}{{AC}} = \frac{{DC}}{{DB}}.\)
\(\frac{{AB}}{{AC}} = \frac{{BD}}{{BC}}.\)
\(\frac{{AB}}{{AC}} = \frac{{DC}}{{BC}}.\)
Tìm \(x\) trong hình vẽ dưới đây: 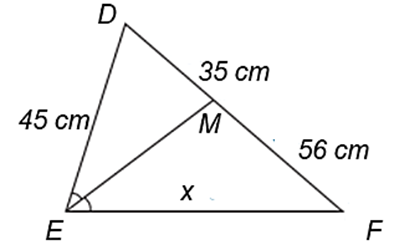
\(x = 62\;{\rm{cm}}.\)
\(x = 72\;{\rm{cm}}.\)
\(x = 70\;{\rm{cm}}.\)
\(x = 60\;{\rm{cm}}.\)
Cho \(\Delta ABC\) có \(E\) là một điểm thuộc cạnh \(BC\) thỏa mãn \(\frac{{CE}}{{BE}} = \frac{{AC}}{{AB}}.\) Khi đó:
\(AE\) là đường phân giác của \(\Delta ABC.\)
\(AE\) là đường trung trực của \(\Delta ABC.\)
\(AE\) là đường cao của \(\Delta ABC.\)
\(AE\) là đường trung tuyến của \(\Delta ABC.\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 4\;{\rm{cm}}{\rm{,}}\;AC = 6\;{\rm{cm}}{\rm{.}}\) Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(\frac{{BD}}{{DC}} = \frac{2}{3}.\) Khi đó:
\(\widehat {DAC} = 60^\circ .\)
\(\widehat {DAC} = 40^\circ .\)
\(\widehat {DAC} = 50^\circ .\)
\(\widehat {DAC} = 45^\circ .\)
Cho \(\Delta ABC\) có \(AB = 10\;{\rm{cm}},\;AC = 16\;{\rm{cm}}.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D.\) Biết rằng \(BD = 8\;{\rm{cm}}{\rm{.}}\) Tính độ dài cạnh \(BC.\)
\(BC = 20\;{\rm{cm}}{\rm{.}}\)
\(BC = 20,4\;{\rm{cm}}{\rm{.}}\)
\(BC = 20,8\;{\rm{cm}}{\rm{.}}\)
\(BC = 20,6\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta OEF\) có \(OM\;\left( {M \in EF} \right)\) là tia phân giác của tam giác. Biết rằng: \(\frac{{OE}}{{OF}} = \frac{4}{3}.\) Khi đó:
\(EM = \frac{4}{3}MF.\)
\(EM = \frac{3}{7}MF.\)
\(EM = \frac{3}{4}MF.\)
Cả A, B, C đều sai.
Cho \(\Delta ABC.\) Tia phân giác góc \(A\) và tia phân giác góc \(B\) của \(\Delta ABC\) cắt nhau tại \(D.\) Gọi \(E\) là giao điểm của \(CD\) và \(AB.\) Khi đó:
\(\frac{{EA}}{{BE}} = \frac{{BC}}{{AC}}.\)
\(\frac{{EA}}{{BE}} = \frac{{AC}}{{BC}}.\)
\(\frac{{EA}}{{BE}} = \frac{{AC}}{{AB}}.\)
\(\frac{{EA}}{{BE}} = \frac{{AB}}{{AC}}.\)
Cho \(\Delta ABC\) có \(AE\;\left( {E \in BC} \right)\) là đường phân giác của tam giác. Gọi \(I\) là điểm nằm trên cạnh \(AB\) sao cho \(\frac{{AI}}{{BI}} = \frac{{AC}}{{BC}}.\) Gọi \(D\) là giao điểm của \(AE\) và \(CI.\) Khi đó:
\(\widehat {ABD} = \frac{2}{3}\widehat {DBC}.\)
\(\widehat {ABD} = \frac{4}{5}\widehat {DBC}.\)
\(\widehat {ABD} = \frac{3}{4}\widehat {DBC}.\)
\(\widehat {ABD} = \widehat {DBC}.\)
Cho hình bình hành \(ABCD\) có \(AD = 10\;{\rm{cm}},\;DC = 8\;{\rm{cm}}.\) Tia phân giác \(\widehat {ABC}\) cắt \(AC\) tại \(E.\) Tính tỉ số \(\frac{{EC}}{{AE}}.\)
\(\frac{2}{3}.\)
\(\frac{3}{4}.\)
\(\frac{3}{5}.\)
\(\frac{4}{5}.\)
Cho hình vẽ:
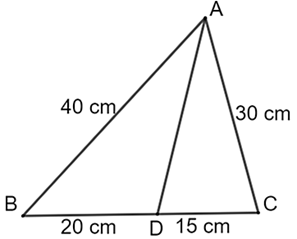
\(\widehat {BAC} = 3\widehat {DAC}.\)
\(\widehat {BAC} = 2\widehat {DAC}.\)
\(\widehat {BAC} = \frac{5}{2}\widehat {DAC}.\)
\(\widehat {BAC} = \frac{3}{2}\widehat {DAC}.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d)
Cho \(\Delta ABC\) có các đường phân giác \(AD,\;BE,\;CF\;\left( {D \in BC,\;E \in AC,\;F \in AB} \right).\)
a) \(\frac{{IA}}{{ID}} = \frac{{BD}}{{BA}}.\)
b) \(\frac{{AD}}{{ID}} = \frac{{AB + BD}}{{BD}}.\)
c) \(\frac{{AD}}{{ID}} = \frac{{CA + CD}}{{CD}}.\)
d) \(\frac{{DI}}{{DA}} = \frac{{AC}}{{AB + BC + CA}}.\)
Cho \(\Delta ABC\) cân tại \(B.\) Kẻ các đường phân giác \(AM\;\left( {M \in BC} \right),\;CN\;\left( {N \in AB} \right).\)
a) \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}.\)
b) \(\frac{{BN}}{{AN}} = \frac{{AC}}{{BC}}.\)
c) \(MN\;{\rm{//}}\;AC.\)
d) Tứ giác \(MNAC\) là hình thang cân.
Cho \(\Delta ABC\) vuông cân tại \(A.\) Kẻ \(BE\;\left( {E \in AC} \right)\) là tia phân giác của \(\widehat {ABC}\) và \(AH \bot BC\;\left( {H \in BC} \right).\) Goi \(I\) là giao điểm của \(AH\) và \(BE.\)
a) \(AI > AE.\)
b) \(\frac{{AB}}{{IA}} = \frac{{BH}}{{HI}}.\)
c) \(\frac{{BH}}{{IH}} = \frac{{BC}}{{EC}}.\)
d) \(EC = 3IH.\)
Cho \(\Delta ABC\) vuông cân tại \(A.\) Kẻ \(BE\;\left( {E \in AC} \right)\) là tia phân giác của \(\widehat {ABC}\) và \(AH \bot BC\;\left( {H \in BC} \right).\) Goi \(I\) là giao điểm của \(AH\) và \(BE.\)
a) \(\frac{{FA}}{{FC}} = \frac{{BA}}{{BC}}.\)
b) \(\frac{{EB}}{{ED}} = \frac{{FA}}{{FC}}.\)
c) \(\frac{{OD}}{{ED}} > \frac{{OC}}{{FC}}.\)
d) \(EF\;{\rm{//}}\;AB\;{\rm{//}}\;CD.\)
Nhà bạn Minh ở vị trí \(M,\) nhà bạn Dũng ở vị trí \(B\) (như hình vẽ), biết rằng tứ giác \(ABCD\) là hình vuông và \(M\) là trung điểm của \(CD.\) Hai bạn đi xe đạp với cùng một vận tốc trên con đường \(BM\) để đi đến điểm \(E.\) Bạn Minh xuất phát lúc \(13\) giờ và hai bạn gặp nhau lúc \(13\) giờ \(30\) phút tại điểm \(E.\)
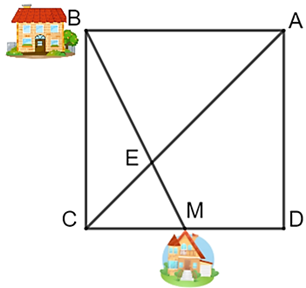
a)\(\frac{{CM}}{{CB}} = \frac{1}{2}.\)
b)\(BE = 2EM.\)
c) Thời gian bạn Dũng đi gấp hai lần thời gian bạn Minh đi khi hai bạn gặp nhau tại điểm \(E.\)
d)Bạn Dũng cần xuất phát lúc \(12\) giờ thì hai bạn gặp nhau tại điểm \(E\) lúc \(13\) giờ \(30\) phút.
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Cho \(\Delta ABC\) có \(AB = 5\;{\rm{cm}},\;AC = 6\;{\rm{cm}},\;BC = 8\;{\rm{cm}}.\) Tia phân giác góc \(B\) cắt \(AC\) tại \(E.\) Độ dài đoạn thẳng \(AE\) bằng bao nhiêu \({\rm{cm?}}\) (Làm tròn kết quả đến hàng phần mười).
Cho \(\Delta ABC\) có \(AB = AC = 12\;{\rm{cm}}{\rm{.}}\) Tia phân giác của góc \(B\) cắt đường cao \(AH\;\left( {H \in BC} \right)\) của \(\Delta ABC\) tại \(I.\) Biết rằng \(\frac{{AI}}{{AH}} = \frac{3}{5}.\) Tính chu vi \(\Delta ABC.\) (Đơn vị: \({\rm{cm}}\)).
Cho \(\Delta ABC\) có chu vi bằng \(148\;{\rm{cm}}{\rm{.}}\) Đường phân giác góc \(A\) cắt \(BC\) tại \(D\) sao cho \(\frac{{BD}}{{BC}} = \frac{2}{5}.\) Đường phân giác góc \(C\) cắt \(AB\) tại \(E\) sao cho \(\frac{{AE}}{{AB}} = \frac{5}{9}.\) Độ dài cạnh \(BC\) bằng bao nhiêu
Cho \(\Delta ABC\) có \(\widehat B = 50^\circ \) và \(I\) là trung điểm của \(BC.\) Tia phân giác của góc \(AIB\) và tia phân giác góc \(AIC\) cắt các cạnh \(AB,\;AC\) lần lượt tại \(M,\;N.\) Số đo \(\widehat {AMN}\) bằng bao nhiêu độ?
Cho \(\Delta ABC\) có \(AB = 4\;{\rm{cm}},\;AC = 6\;{\rm{cm}}\) và đường phân giác \(AD\;\left( {D \in BC} \right).\) Qua \(D\) kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E.\) Khi đó, \(AC = ...AE.\) Tìm số thích hợp để điền vào “…”.


