10 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
((Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Trong các hình dưới đây, có hình nào là hình chữ nhật?
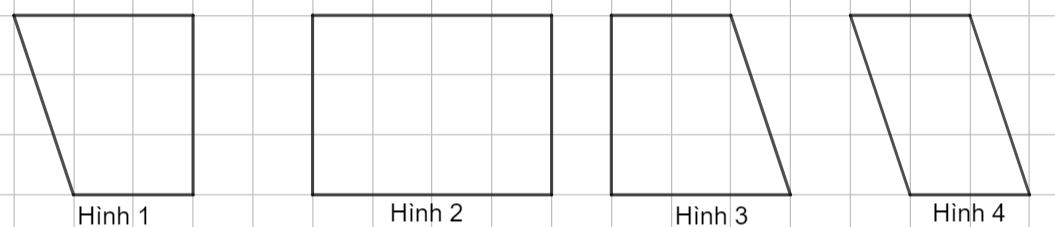
Hình \(1.\)
Hình \(2.\)
Hình \(3.\)
Hình \(4.\)
Trong hình chữ nhật:
Hai đường chéo vuông góc với nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Cả A và B đều đúng.
Cả A và B đều sai.
Trong tam giác vuông:
Trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Trung tuyến ứng với cạnh huyền bằng cạnh huyền.
Trung tuyến ứng với cạnh huyền bằng một phần ba cạnh huyền.
Trung tuyến ứng với cạnh huyền bằng hai lần cạnh huyền.
Cho hình chữ nhật \(ABCD\) có \(BD = 7\;{\rm{cm}}{\rm{.}}\) Khi đó:
\(AC = 3,5\;{\rm{cm}}{\rm{.}}\)
\(AC = 14\;{\rm{cm}}{\rm{.}}\)
\(AC = 7\;{\rm{cm}}{\rm{.}}\)
\(AC = 9\;{\rm{cm}}{\rm{.}}\)
Cho tứ giác \(ABCD\) có \(\widehat A = \widehat B = \widehat C = \widehat D,\;CB = 5\;{\rm{cm}}.\) Khi đó:
\(AD = 4\;{\rm{cm}}{\rm{.}}\)
\(AD = 6\;{\rm{cm}}{\rm{.}}\)
\(AD = 5\;{\rm{cm}}{\rm{.}}\)
\(AD = 10\;{\rm{cm}}{\rm{.}}\)
Chọn đáp án đúng:
Hình thang có hai góc vuông là hình chữ nhật.
Hình thang có hai đường chéo bằng nhau là hình chữ nhật.
Hình thang cân có một góc vuông là hình chữ nhật.
Cả A, B, C đều đúng.
Cho hình bình hành \(ABCD.\)Nếu \(\widehat A = 90^\circ \) thì:
\(AC = \frac{1}{2}BD.\)
\(AC = \frac{3}{4}BD.\)
\(AC = \frac{4}{3}BD.\)
\(AC = BD.\)
Chọn câu sai:
Hình bình hành có một góc vuông là hình chữ nhật.
Tứ giác có ba góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo vuông góc với nhau là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Cho hình chữ nhật \(ABCD\) có hai đường chéo cắt nhau tại \[O.\] Khi đó:
\(\widehat {OAB} = \widehat {OBA}.\)
\(\widehat {OAB} = 2\widehat {OBA}.\)
\(\widehat {OAB} = \frac{1}{2}\widehat {OBA}.\)
\(\widehat {OAB} = \frac{1}{3}\widehat {OBA}.\)
Cho tứ giác \(ABCD\) có \(\widehat A = \widehat B = \widehat C = 90^\circ \) và chu vi bằng \(30\;{\rm{cm}}.\) Khi đó, tổng độ dài hai cạnh \(AB\) và \(AD\) bằng:
\(18\;{\rm{cm}}.\)
\(24\;{\rm{cm}}.\)
\(25\;{\rm{cm}}.\)
\(15\;{\rm{cm}}.\)
