20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Ôn tập chương 8 (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong các phát biểu sau, phát biểu nào đúng?
Hai tam giác đồng dạng thì bằng nhau.
Hai tam giác bằng nhau thì không đồng dạng.
Hai tam giác bằng nhau thì đồng dạng.
Hai tam giác vuông luôn đồng dạng với nhau.
Cho tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'.\) Phát biểu nào sau đây là sai?
\(\widehat {A\,} = \widehat {C'}.\)
\(\widehat {B\,} = \widehat {B'}.\)
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}.\)
\(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}.\)
Nếu \(\Delta ABC \sim \Delta DEF\) theo tỉ số \(k\) thì \(\Delta DEF \sim \Delta ABC\) theo tỉ số bằng
\(k.\)
\(\frac{1}{k}.\)
\({k^2}.\)
\(\frac{1}{{{k^2}}}.\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \[\frac{{AB}}{{DF}} = \frac{{AC}}{{DE}} = \frac{{BC}}{{EF}}\] thì
\[\Delta ABC \sim \Delta DEF.\]
\[\Delta ABC \sim \Delta DFE.\]
\[\Delta ABC \sim \Delta EDF.\]
\[\Delta ABC \sim \Delta EFD.\]
Nếu \(\Delta ABC\) có \[MN\,{\rm{//}}\,AB\] (với \[M \in BC\] và \[N \in CA)\] thì
\(\Delta AMN \sim \Delta ABC.\)
\(\Delta ABC \sim \Delta MNC.\)
\(\Delta NMC \sim \Delta ABC.\)
\(\Delta CAB \sim \Delta CMN.\)
Cho \(\Delta ABC \sim \Delta DEF\) với tỉ số bằng \(\frac{1}{2}\) và \[\widehat {A\,} = 80^\circ ;\]\[\widehat {B\,} = 70^\circ ;\]\[\widehat {F\,} = 30^\circ ;\]\[BC = 6\,\,{\rm{cm}}.\] Khẳng định nào sau đây là đúng?
\[EF = 6\,\,{\rm{cm}}{\rm{.}}\]
\[\widehat {E\,} = 80^\circ .\]
\[\widehat {D\,} = 70^\circ .\]
\[\widehat {C\,} = 30^\circ .\]
Cho \(\Delta ABC \sim \Delta MNP\)theo tỉ số là \(\frac{2}{3},\) biết chu vi của \(\Delta ABC\)bằng \[40{\rm{\;cm}}.\]Khi đó chu vi của \(\Delta MNP\)bằng
\(20{\rm{\;cm}}.\)
\(30{\rm{\;cm}}.\)
\(45{\rm{\;cm}}.\)
\[60{\rm{\;cm}}.\]
Cho \(\Delta ABC \sim \Delta MNP\). Biết \(AB = 5\,\,{\rm{cm}},\,\,BC = 6\,\,{\rm{cm}},\,\,MN = 10\,\,{\rm{cm}}.\) Khẳng định nào dưới đây là đúng?
\(NP = 2,5\,\,{\rm{cm}},\,\,AC = 12\,\,{\rm{cm}}.\)
\(NP = 5\,\,{\rm{cm}},\,\,AC = 10\,\,{\rm{cm}}.\)
\(NP = 12\,\,{\rm{cm}},\,\,AC = 2,5\,\,{\rm{cm}}.\)
\(NP = 10\,\,{\rm{cm}},\,\,AC = 5\,\,{\rm{cm}}.\)
Cho \(\Delta ABC \sim \Delta MNP\) theo tỉ số đồng dạng \(k = 2,\) biết \(AB = 6\,\,{\rm{cm}}{\rm{.}}\) Độ dài cạnh \(MN\) là
3 cm.
6 cm.
24 cm.
8 cm.
Cho hình vẽ và các khẳng định sau:
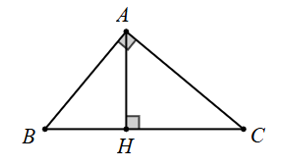
(I). \(\Delta AHB \sim \Delta CHA\,\,\left( {{\rm{g}}{\rm{.g}}} \right)\); (II). \(\Delta AHC \sim \Delta BAC\,\,\left( {{\rm{g}}{\rm{.g}}} \right)\).
Khi đó:
(I) đúng.
(II) đúng.
Cả (I) và (II) đều sai.
Cả (I) và (II) đều đúng.
Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AM\), \(N\) là trung điểm của \(AC\). Kẻ \(Ax\parallel BC\) cắt \(MN\) tại \(E\).
\(M\) là trung điểm của \(BC.\)
\(ME\parallel AB.\)
\(AE = MC.\)
\(\Delta AEN \sim \Delta CNM\).
Cho nhọn \(\left( {AB < AC} \right)\), đường cao \(AH\). Gọi \(D,E\) lần lượt là hình chiếu của \(H\) trên \(AB,AC\). Biết \(AH = 5{\rm{ cm,}}\)\(DE = 4{\rm{ cm,}}\)\(BC = 8{\rm{ cm}}\).
\(\Delta ADH \sim \Delta AHB\).
\(A{H^2} = AD.AB\).
\(\Delta ADE \sim \Delta CAB\).
\({S_{ADE}} = 5{\rm{ c}}{{\rm{m}}^2}\).
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm;}}\)\(BC = 8{\rm{ cm;}}\)\(AC = 6{\rm{ cm}}\). Một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) theo thứ tự \(M,N\) sao cho \(BM = AN\).
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
\(\Delta ABC \sim \Delta ANM\)
\(AN = 2,4{\rm{ cm}}\), \(MN = 3,2{\rm{ cm}}\).
\(\frac{{{S_{ANM}}}}{{{S_{ABC}}}} = \frac{4}{{25}}\).
Cho tam giác \(ABC\). Trên cạnh \(AB,AC\) lần lượt lấy các điểm \(E,D\) sao cho \(AC = 3AE\) và \(AD = \frac{1}{3}AB\). Gọi \(I\) là giao điểm của \(BD\) và \(EC\). Biết rằng .
\(\widehat {ADB} = \widehat {AEC}\).
\(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\).
\(\Delta ADE \sim \Delta ACB\).
\(ID.IB = IE.IC\).
Cho \(\Delta ABC\) có \(AB = 2{\rm{ cm,}}\)\(AC = 4{\rm{ cm}}\). Qua \(B\) dựng đường thẳng cắt \(AC\) tại \(D\) sao cho \(\widehat {ABD} = \widehat {ACB}\). Gọi \(AH\) là đường cao \(\Delta ABC\), \(AE\) là đường cao của \(\Delta ABD\).
\(\Delta ABD \sim \Delta ACB\)
\(\widehat {ADB} = \widehat {ABC}\).
\(AD = 1{\rm{ cm,}}\)\(DC = 2{\rm{ cm}}\).
\({S_{ABH}} = 4{S_{ADE}}\).
Cho tam giác \[ABC\] vuông tại \(A,\) kẻ \(AH \bot BC\)\(\left( {H \in BC} \right).\) Biết \(BC = 20{\rm{\;cm}}\) và \(AC = 12{\rm{\;cm}},\) độ dài cạnh \(BH\) bằng bao nhiêu? (Đơn vị: cm, kết quả ghi dưới dạng số thập phân)
Biết rằng \(\Delta ABC \sim \Delta HIK,\;\,\widehat A = 90^\circ ,\;\,AB = 2HI.\) Hỏi tỉ số diện tích \(\frac{{{S_{HIK}}}}{{{S_{ABC}}}}\) bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ, biết \(KC = 1,5\,\,{\rm{cm}};\,\,\,KI = 3\,\,{\rm{cm}}{\rm{.}}\)
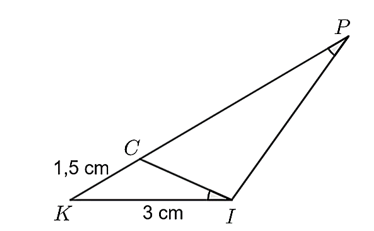
Hỏi độ dài \(CP\) bằng bao nhiêu centimet? (Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ, biết \(NC = 1,5\,\,{\rm{cm, }}AN = 2\,\,{\rm{cm}}{\rm{.}}\)
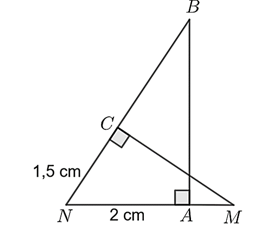
Tính tỉ số \(\frac{{MN}}{{NB}}\). (Kết quả ghi dưới dạng số thập phân)
Cho hai tam giác \(ABC\) và \(FDE\) như hình vẽ dưới đây:
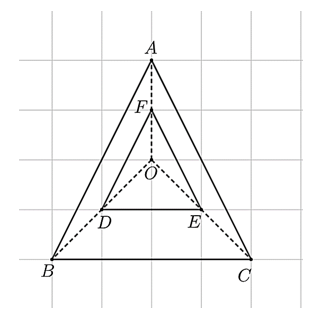
Tam giác \(FDE\) là hình đồng dạng phối cảnh với tam giác \(ABC\) tâm \(O\) với tỉ số đồng dạng là bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
