20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Ôn tập chương 7 (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Chọn khẳng định sai. Cho hình vẽ với \(AB < AC\).
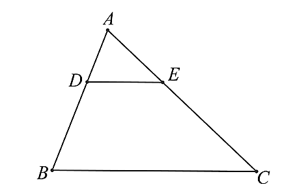
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC\).
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC\).
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{EC}}\) suy ra \(DE\parallel BC\).
\(\frac{{AD}}{{DE}} = \frac{{AE}}{{BC}}\) suy ra \(DE\parallel BC\).
Chọn câu đúng.
Đường trung bình của tam giác là đoạn thẳng nối chân đường cao của tam giác.
Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
Trong một tam giác chỉ có một đường trung bình.
Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.
Cho hình vẽ dưới đây:
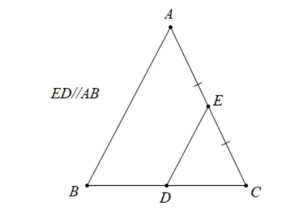
Khẳng định đúng là
\(AE = \frac{1}{2}BC.\)
\(D\) là trung điểm của \(BC.\)
\(DE\) không song song với \(AB.\)
\(DB > DC.\)
Cho hình vẽ sau:
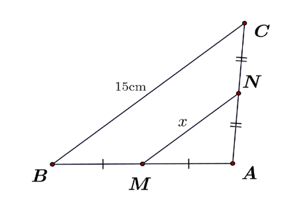
Độ dài của \(x\) là
30 cm.
5,7 cm.
7,5 cm.
8,5 cm.
Viết tỉ số cặp đoạn thẳng độ dài như sau: \(AB = 4{\rm{ dm, }}CD = 20{\rm{ dm}}{\rm{.}}\)
\(\frac{{AB}}{{CD}} = \frac{1}{4}.\)
\(\frac{{AB}}{{CD}} = \frac{1}{5}.\)
\(\frac{{AB}}{{CD}} = \frac{1}{6}.\)
\(\frac{{AB}}{{CD}} = 5.\)
Cho \(\Delta ABC\) có \(H\) là trung điểm của \(BC\), \(K\) là trung điểm của \(AB\) thì đường trung bình của \(\Delta ABC\) là
\(MN.\)
\(AK.\)
\(HK.\)
\(KA.\)
Cho \(\Delta ABC\) có \(H\) là trung điểm của \(BC\), \(K\) là trung điểm của \(AB\) thì khẳng định nào sau đây là sai?
\(HK\parallel BC.\)
\(HK = \frac{1}{2}AC.\)
\(AC = 2KH.\)
\(HK\parallel AC.\)
Cho \(\Delta ABC\), đường phân giác \(AD\) như hình vẽ. Tỉ số \(\frac{x}{y}\) bằng
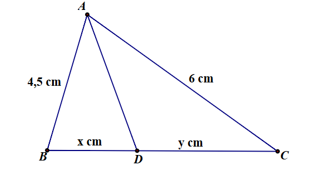
\(\frac{3}{4}.\)
\(\frac{2}{3}.\)
\(\frac{4}{3}.\)
\(\frac{3}{2}.\)
Cho \(\Delta ABC\), \(AD\) là phân giác trong của góc \(A.\) Khẳng định nào sau đây là đúng?
\(\frac{{DC}}{{DB}} = \frac{{AB}}{{AC}}.\)
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}.\)
\(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}.\)
\(\frac{{AD}}{{DB}} = \frac{{AC}}{{AD}}.\)
Cho \(\Delta ABC\), phân giác \(AD{\rm{ }}\left( {D \in BC} \right).\) Biết \(AB = 10{\rm{ cm, }}AC = 19{\rm{ cm, }}BD = 5{\rm{ cm}}\).
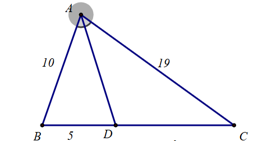
Độ dài của đoạn thẳng \(CD\) bằng:
20 cm.
9,5 cm.
38 cm.
\(\frac{{50}}{{19}}\) cm.
Cho tam giác \(ABC\) nhọn có đường cao \(AH\). Trên \(AH\) lấy các điểm \(K,I\) sao cho \(AK = KI = IH.\) Qua \(K,I\) lần lượt vẽ các đường thẳng \(MN\parallel BC,{\rm{ }}EF\parallel BC\) (\(M,E \in AB,\)\(N,F \in AC\))
\(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}.\)
\(\frac{{EF}}{{BC}} = \frac{3}{2}.\)
\(MNEF\) là hình bình hành.
Biết \({S_{ABC}} = 90{\rm{ c}}{{\rm{m}}^2},\) khi đó \({S_{MNEF}} = 30{\rm{ c}}{{\rm{m}}^2}.\)
Cho hình thang \(ABCD{\rm{ }}\left( {AB\parallel CD} \right)\). Một đường thẳng song song với hai đáy, cắt các cạnh bên \(AD\) và \(BC\) theo thứ tự \(M\) và \(N.\) Gọi \(I\) là giao điểm của đường chéo \(AC\) với \(MN\). Khi đó:
\(\frac{{AM}}{{MD}} = \frac{{AI}}{{IC}}.\)
\(\frac{{AM}}{{MD}} = \frac{{BN}}{{BC}}.\)
\(\frac{{CN}}{{CB}} = \frac{{CI}}{{CA}}.\)
\(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1\).
Cho hình chữ nhật \(ABCD\) có \(AB = 2AD.\) Vẽ \(BH \bot AC\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AH,BH,CD.\) Gọi \(I\) là trung điểm của \(BP,{\rm{ }}J\) là giao điểm của \(MC\) và \(NP.\)
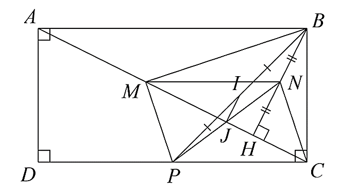
Khi đó,
\(MN\parallel CP.\)
\(N\) là trực tâm của \(\Delta BCM.\)
\(BM \bot MP.\)
\[2IJ = HB\].
Cho \(\Delta ABC\) nhọn \(\left( {AB < AC} \right)\), trung tuyến \(AD\). Vẽ tia phân giác \(\widehat {ADB}\) cắt \(AB\) tại \(M,\) tia phân giác \(\widehat {ADC}\) cắt \(AC\) tại \(N\). Khi đó:
\(\frac{{MB}}{{MA}} = \frac{{BD}}{{DA}}.\)
\(\frac{{NC}}{{NA}} = \frac{{DC}}{{DA}}.\)
\(\frac{{MB}}{{MA}} = \frac{{NA}}{{NC}}.\)
\(MN\parallel BC.\)
Cho tam giác \(ABC\), điểm \(I\) nằm trong tam giác, các tia \(AI,BI,CI\) cắt các cạnh \(BC,AC,AB\) theo thứ tự ở \(D,E,F\). Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt tia \(CI\) tại \(H\) và cắt tia \(BI\) tại \(K\).
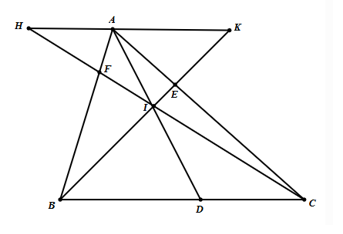
Khi đó:
\(\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}}\).
\(\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{HK}}{{BC}}.\)
\(\frac{{AE}}{{CE}} + \frac{{AF}}{{BF}} = \frac{{AI}}{{ID}}\).
\(\frac{{BD}}{{DC}} \cdot \frac{{EC}}{{EA}} \cdot \frac{{FA}}{{FB}} = 3.\)
Giữa hai điểm \(B\) và \(C\) có một cái ao. Để đo khoảng cách \(BC\) người ta đo được các đoạn thẳng \(AD = {\rm{2 m, }}BD = 10{\rm{ m}}\) và \(DE = 5{\rm{ m}}{\rm{.}}\)
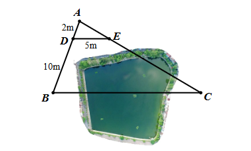
Biết \(DE\parallel BC\), tính khoảng cách giữa hai điểm \(B\) và \(C.\)
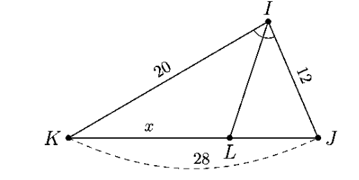
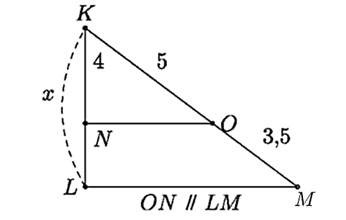
Tìm độ dài của \(x\) trong hình vẽ dưới đây. (Kết quả ghi dưới dạng số thập phân)
Người ta dùng máy ảnh để chụp vật \(AB\) cao 120 cm (như hình vẽ). Sau khi tráng phim thấy ảnh cao 3 cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \(5{\rm{ cm}}{\rm{.}}\)
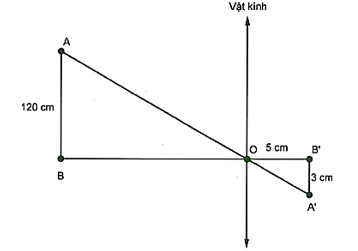
Hỏi vật \(AB\) được đặt cách vật kính máy ảnh là bao nhiêu mét?
Cho hĩnh vẽ dưới đây, biết \(AB\parallel EF;{\rm{ }}AF = 44,5{\rm{ cm; }}FC = 44,2{\rm{ cm; }}EF = 18,6{\rm{ cm}}{\rm{.}}\)
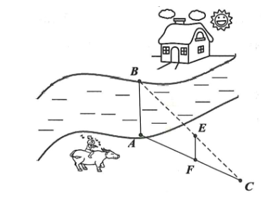
Tính chiều rộng khúc sông \(AB\). (làm tròn đến chữ số thập phân thứ nhất)
Tính độ dài của \(x\) trong hình dưới đây. (Kết quả ghi dưới dạng số thập phân)