20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Ôn tập chương 5 (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong các hàm số sau, hàm số nào không là hàm số bậc nhất?
\(y = 4 - x.\)
\(y = \frac{{1 + 2x}}{2}.\)
\(y = {x^2} + x.\)
\(y = \frac{1}{2}x - 3.\)
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = - \frac{1}{2}x + 1?\)
\(\left( {1;\frac{1}{2}} \right).\)
(B. \(\left( {3;3} \right).\)
\(\left( { - 1;\frac{1}{2}} \right).\)
\(\left( { - 2; - 1} \right).\)
Đường thẳng \[y = 1-3x\] có hệ số góc là
\( - 3.\)
\( - 1.\)
\(1.\)
\(3.\)
Cho hình vẽ bên. Đường thẳng \[OA\] là đồ thị của hàm số
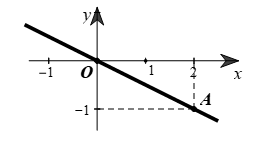
\[y = --2x.\]
\[y = -0,5x.\]
\(y = \frac{1}{2}x.\)
\[y = 2x.\]
Đường thẳng có hệ số góc bằng \[-4\]và đi qua điểm \[A\left( {3;-2} \right)\] là
\[y = -4x + 10.\]
\[y = 4x + 10.\]
\[y = -4x--10.\]
\[y = -4x.\]
Cho hai hàm số \[y = \left( {m + 3} \right)x-m\]và \[y = 3x-3m + 2.\] Giá trị của \[m\] để đồ thị của hai hàm số trên vuông góc với nhau là
\[\frac{{10}}{3}.\]
\[-\frac{{10}}{3}.\]
\(\frac{8}{3}.\)
\( - \frac{8}{3}.\)
Hai đường thẳng \[y = x + 2\] và \[y = 2x + 2\] trên cùng một mặt phẳng tọa độ có vị trí tương đối là
Trùng nhau.
Cắt nhau tại điểm có tung độ là 2
Song song với nhau.
Cắt nhau tại điểm có tung độ là \[-2.\]
Hai đường thẳng \(y = \left( {m - 1} \right)x + 2\,\,\left( {m \ne 1} \right)\) và \(y = 3x + 2\) trùng nhau khi
\(m = - 4.\)
\(m = - 2.\)
\(m = 4.\)
\(m \ne - 4.\)
Nếu hai đường thẳng \[y = -3x + 4\]và \[y = \left( {m + 2} \right)x + m\] song song với nhau thì giá trị của \[m\] bằng
\[-5.\]
\[-3.\]
\[-2.\]
\[3.\]
Góc tạo bởi đường thẳng \(y = 5 - 4x\) với trục \[Ox\] là
góc nhọn.
góc vuông.
góc tù.
góc bẹt.
Cho ba đường thẳng \(\left( {{d_1}} \right):y = - 2x,\)\(\left( {{d_2}} \right):y = 1,5x + 7\) và \(\left( {{d_3}} \right):y = - 2mx + 5.\)
Hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng \( - 2.\)
\(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( { - 2;4} \right).\)
Để \(\left( {{d_3}} \right)\) cắt \(\left( {{d_1}} \right)\) thì \(m \ne - \frac{3}{4}.\)
ba đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right)\) cắt nhau tại một điểm thì \(m = \frac{1}{4}.\)
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x + 1,\)\(\left( {{d_2}} \right):y = x + 1\).
Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cắt nhau.
Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right).\)
Đường thẳng \(\left( {{d_3}} \right)\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\) là \(y = 2x - 1.\)
Đường thẳng \(\left( {{d_4}} \right)\) đi qua \(A\), cắt đường thẳng \(\left( {{d_2}} \right)\) và có hệ số góc là \(3\) là đường thẳng \(y = 3x + 1.\)
Cho hàm số \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\).
Điều kiện để hàm số trên là hàm bậc nhất là \(m = 2.\)
Với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) đi qua điểm \(A\left( {0;4} \right).\)
Để \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(m = 3.\)
Để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1.\)
Cho hàm số \(\left( d \right):y = 2x + 4\) và \(\left( {d'} \right):y = \left( {m - 2} \right)x + m + 2.\)
Với \(m = 0\) thì hai đường thẳng cắt nhau.
Với \(m = 2\) thì hai đường thẳng song song.
Khi \(m = 0\) thì hai đường thẳng cùng đi qua điểm \(M\left( {\frac{1}{2};3} \right).\)
Để hai đường thẳng cắt nhau tại một điểm thuộc trục hoành thì \(m = 6.\)
Cho hai đường thẳng \(\left( d \right):y = 4x + m\) và \(\left( {d'} \right):y = - 3x + 2 - m\).
Hai đường thẳng luôn cắt nhau với mọi giá trị của \(m.\)
Với \(m = - 4\) thì chỉ đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1;0} \right)\).
Với \(m = 4\) thì hai đường thẳng cắt nhau tại điểm \(\left( {\frac{6}{7};\frac{4}{7}} \right).\)
Điều kiện của \(m\) để hai đường thẳng \(\left( d \right),\left( {d'} \right)\) cắt nhau tại 1 điểm nằm bên phải trục tung là \(m < 1.\)
Cho hàm số \[f\left( x \right) = - \left| {2 - \frac{1}{2}x} \right|.\] Giá trị \[f\left( {-2} \right)\] bằng bao nhiêu?
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\).
Cho hàm số bậc nhất \[y = x + {m^2} + 1\] và \[y = 5 + \left( {m-1} \right)x.\]Giá trị của \[m\]để đồ thị hai hàm số cắt nhau tại một điểm trên trục tung là
Biết đường thẳng \(d:y = \left( {m + 2} \right)x - 5\) đi qua điểm \(A\left( { - 1;2} \right).\) Hỏi hệ số góc của đường thẳng đó bằng bao nhiêu?
Cho hai hàm số \[y = x + m + 1\] và \[y = 3 + \left( {m-1} \right)x.\]Với giá trị nào của \[m\]để đồ thị hai hàm số trên cắt nhau tại một điểm trên trục hoành?
