20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Ôn tập chương 3 (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho tứ giác \(ABCD\) như hình vẽ dưới đây.
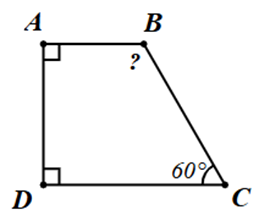
Số đo của \(\widehat B\) là
\(110^\circ .\)
\(120^\circ .\)
\(130^\circ .\)
\(140^\circ .\)
Cho hình thang cân \(ABCD\) có \(AB\parallel CD\) và \(\widehat A = 125^\circ \). Khi đó, góc \(B\) bằng
\(125^\circ .\)
\(65^\circ .\)
\(90^\circ .\)
\(55^\circ .\)
Khẳng định nào sau đây là sai?
Tứ giác có hai cặp cạnh đối song song là hình bình hành.
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Hình thang có hai đường chéo bằng nhau là hình bình hành.
Cho hình vẽ sau.
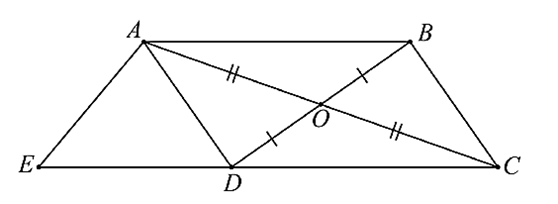Hãy chọn khẳng định sai.
\(ABCD\) là hình bình hành.
\(\Delta ABC = \Delta CDA\).
\(ABCD\) là hình thang cân.
\(BC\parallel AD.\)
Hình thang cân cần thêm điều kiện nào sau đây để trở thành hình chữ nhật?
Có hai đường chéo bằng nhau.
Có hai đường chéo vuông góc.
Có hai góc kề một đáy bằng nhau.
Có một góc vuông.
Cho hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = 50^\circ \), khi đó số đo của \[\widehat {ABO}\] là
\(25^\circ .\)
\(50^\circ .\)
\(90^\circ .\)
\(130^\circ .\)
Hình bình hành cần có thêm điều kiện nào sau đây để trở thành hình thoi?
Có một góc vuông.
Có hai cạnh kề bằng nhau.
Có hai đường chéo bằng nhau.
Có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Cho hình thoi \(ABCD\). Biết đường cao \(AH\) kẻ từ đỉnh \(A\) đến cạnh \(CD\) chia cạnh đó thành hai đoạn bằng nhau.
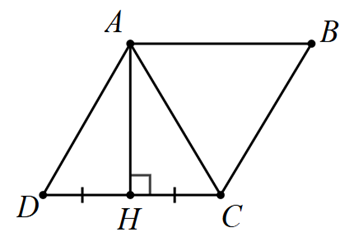
Số đo các góc của hình thoi là
\(\widehat B = \widehat D = 80^\circ ,\widehat A = \widehat C = 100^\circ .\)
\(\widehat B = \widehat D = 120^\circ ,\widehat A = \widehat C = 60^\circ .\)
\(\widehat B = \widehat C = 60^\circ ,\widehat A = \widehat D = 120^\circ .\)
\(\widehat B = \widehat D = 60^\circ ,\widehat A = \widehat C = 120^\circ .\)
Cho hình vẽ dưới đây.
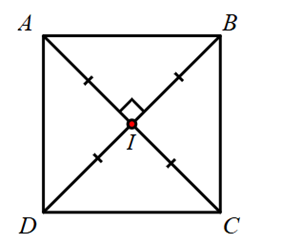
Tứ giác \(ABCD\) là hình vuông theo dấu hiệu nào?
Hình thoi có một góc vuông.
Hình chữ nhật có hai đường chéo bằng nhau.
Hình bình hành có hai đường chéo bằng nhau.
Hình thoi có hai đường chéo bằng nhau.
Một hình vuông có chu vi là 32 cm. Diện tích hình vuông bằng
\(49{\rm{ c}}{{\rm{m}}^2}.\)
\(64{\rm{ c}}{{\rm{m}}^2}.\)
\(14{\rm{ c}}{{\rm{m}}^2}.\)
\(32{\rm{ c}}{{\rm{m}}^2}.\)
Cho tứ giác \(ABCD\) có \(\widehat B + \widehat D = 180^\circ \) và \(CB = CD\). Trên tia đối của tia \(DA\) lấy điểm \(E\) sao cho \(ED = AB\).
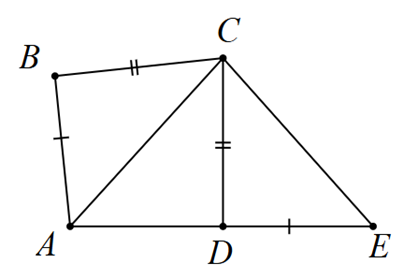
a) \(\widehat {ABC} = \widehat {EDC}.\)
b) \(\Delta ABC = \Delta DEC\).
c) \(\Delta CAE\) là tam giác cân.
d) \(AC\) là tia phân giác của \(\widehat {BAD}\).
Cho hình bình hành \(ABCD\), đường chéo \(BD.\) Kẻ \(AH\) và \(CK\) vuông góc với \(BD\) lần lượt tại \(H\) và \(K.\) Gọi \(M\) là giao điểm của \(AK\) và \(BC\), gọi \(N\) là giao điểm của \(CH\) và \(AD\) và \(O\) là trung điểm của \(BD\).
a) \(\Delta ADH = \Delta CKB\).
b) \(AK\parallel CH.\)
c) \(AM = CN.\)
d) \(M,O,N\) thẳng hàng.
Cho hình thoi \(ABCD\) có \(\widehat A = 60^\circ \), kẻ \(BH \bot AD{\rm{ }}\left( {H \in AD} \right)\), rồi kéo dài một đoạn \(HE = HB.\) Nối \(E\) với \(A\), \(E\) với \(D\).
a) \(H\) là trung điểm của \(AD\).
b) \(ABDE\) là hình thoi.
c) \(D\) là trung điểm \(CE.\)
d) \(AC > BE.\)
Cho hình vuông \(ABCD.\) Lấy các điểm \(E,F\) theo thứ tự thuộc các cạnh \(CD,DA\) sao cho \(DE = AF.\) Gọi \(I\) là giao điểm của \(AE\) và \(BE\).
a) \(\Delta AED = \Delta BAF.\)
b) \(AE = BF.\)
c) \(\widehat {BAF} = \widehat {DAE}\).
d) \(AE \bot BF.\)
Cho hình vuông \(ABCD.\) Trên cạnh \(AB,BC,CD,DA\) lần lượt lấy các điểm \(E,F,G,H\) sao cho \(AE = BF = CG = DH\).
a) \(AH = BE = CF = DG.\)
b)\(\Delta AEH = \Delta BEF\).
c) \(\widehat {FEH} < 90^\circ \).
d) \(EFGH\) là hình vuông.
Cho tứ giác \(ABCD\) có \(AB\parallel CD,\)\[\widehat {ABC} = 135^\circ ,{\rm{ }}\widehat {ACB} = 24^\circ ,{\rm{ }}\widehat {ADC} = 60^\circ \]. Hỏi số đo của \(\widehat {DAC}\) bằng bao nhiêu độ?
Cho hình thang cân \(ABCD{\rm{ }}\left( {AB\parallel CD} \right)\), kẻ đường cao \(AH,BK\) của hình thang, biết \(AB = 2{\rm{ cm; }}AH = 4{\rm{ cm; }}\widehat D = 45^\circ \).
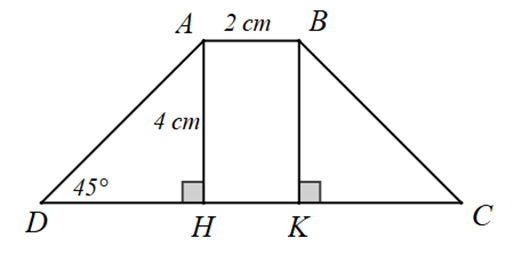
Tính diện tích của hình thang cân \(ABCD\). (Đơn vị: \({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Cho tứ giác \(ABCD\) như hình vẽ dưới đây, biết \(\widehat C = 90^\circ ,\widehat A = 120^\circ \).
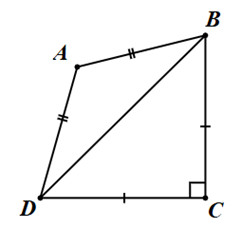
Hỏi số đo của \(\widehat {ABC}\) bằng bao nhiêu độ?
Cho hình vẽ sau:
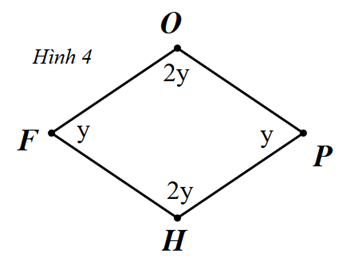
Hỏi giá trị của \(y\) bằng bao nhiêu độ?
Cho hình vuông \(ABCD.\) Gọi \(M,N,P,Q\) là trung điểm các cạnh \(AB,BC,CD,CA\). Tính tỉ số \(\frac{{{S_{MNPQ}}}}{{{S_{ABCD}}}}\). (Kết quả ghi dưới dạng số thập phân)