20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 4. Hình bình hành – Hình thoi (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong các hình dưới đây, hình nào là hình bình hành?
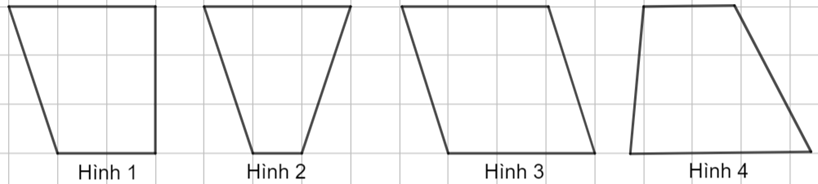
Hình \(1.\)
Hình \(2.\)
Hình \(3.\)
Hình \(4.\)
Trong hình bình hành:
Hai đường chéo vuông góc với nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hai đường chéo bằng nhau.
Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
Cho tứ giác \(HEMF\) như hình vẽ:
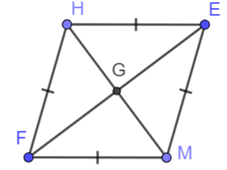
Chọn câu sai:
\(FE \bot HM\) tại \(G.\)
\(EF\) là tia phân giác của \(\widehat {HEM}.\)
\(FE = HM.\)
\(G\) là trung điểm của \(FE.\)
Cho hình bình hành \(ABCD\) có \(\widehat {BAD} = 70^\circ .\) Khi đó:
\(\widehat {BCD} = 60^\circ .\)
\(\widehat {BCD} = 65^\circ .\)
\(\widehat {BCD} = 70^\circ .\)
\(\widehat {BCD} = 75^\circ .\)
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết rằng \(AC = 6\;{\rm{cm}}{\rm{.}}\) Tính độ dài đoạn thẳng \(OA.\)
\(OA = 3\;{\rm{cm}}.\)
\(OA = 4\;{\rm{cm}}.\)
\(OA = 2,5\;{\rm{cm}}.\)
\(OA = 1,5\;{\rm{cm}}.\)
Cho tứ giác \(ABCD\) có: \(\widehat A = \widehat C,\;\widehat B = \widehat D,\;AB = 3\;{\rm{cm,}}\;AD = 5\;{\rm{cm}}{\rm{.}}\) Khi đó:
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{5}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Biết rằng tổng độ dài của hai cạnh kề của một mắt lưới đó bằng \(9\;{\rm{cm}}{\rm{.}}\) Chu vi của một mắt lưới là:
\(18\;{\rm{cm}}.\)
\(24\;{\rm{cm}}.\)
\(25\;{\rm{cm}}.\)
\(15\;{\rm{cm}}.\)
Cho hình thoi \(ABCD\), \(O\) là giao điểm của \(AC\) và \(BD\). Khẳng định nào sau đây là sai?
\(AB = BC = CD = DA.\)
\(AB \bot CD.\)
\(BC\parallel AD.\)
\(O\) là trung điểm của \(AC\) và \(BD.\)
Cho hình thoi \(ABCD\). Biết đường cao \(AH\) kẻ từ đỉnh \(A\) đến cạnh \(CD\) chia cạnh đó thành hai đoạn bằng nhau.
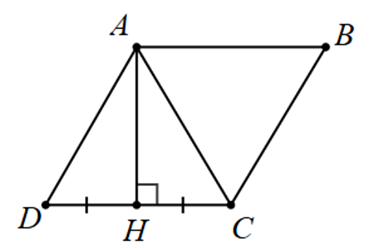Số đo các góc của hình thoi đó là:
\(\widehat B = \widehat D = 80^\circ ,\widehat A = \widehat C = 100^\circ .\)
\(\widehat B = \widehat D = 120^\circ ,\widehat A = \widehat C = 60^\circ .\)
\(\widehat B = \widehat C = 60^\circ ,\widehat A = \widehat D = 120^\circ .\)
\(\widehat B = \widehat D = 60^\circ ,\widehat A = \widehat C = 120^\circ .\)
Cho hình bình hành \(ABCD\) có \(AB = AD.\) Khi đó:
\(\widehat {ABC} = 3\widehat {ABD}.\)
\(\widehat {ABC} = 2\widehat {ABD}.\)
\(\widehat {ABC} = \frac{3}{2}\widehat {ABD}.\)
\(\widehat {ABC} = \frac{4}{3}\widehat {ABD}.\)
Cho tứ giác \(ABCD\) như hình vẽ:
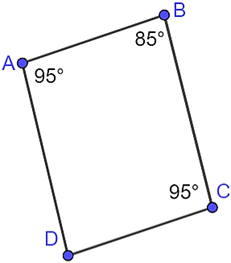
Biết rằng: \(AD - AB = 2\;{\rm{cm}},\;CD = \frac{3}{4}BC\)
a)\(\widehat D = 60^\circ .\)
b)Tứ giác \(ABCD\) là hình bình hành.
c)Gọi \(O\) là giao điểm của hai đường chéo trong tứ giác \(ABCD\) thì \(O\) là trung điểm của \(BD.\)
d)\(AD = 6\;{\rm{cm}}.\)
Cho hình bình hành \(ABCD.\) Gọi \(H,\;K\) lần lượt là hình chiếu vuông góc của \(A,\;C\) trên \(BD.\)
a)\(\widehat {ADB} = \widehat {DBC}.\)
b)\(\Delta DHA = \Delta BKC.\)
c)Tứ giác \(AKCH\) là hình bình hành.
d)\(\widehat {KAB} > \widehat {HCD}.\)
Cho tứ giác \(ABCD\) có \(AB = CD,\;AB\;{\rm{//}}\;CD,\;AB = 2AD.\) Gọi \(E,\;F\) lần lượt là trung điểm của \(AB,\;DC.\)
a) Tứ giác \(ABCD\) là hình thoi.
b)\(AE = AD.\)
c)Tứ giác \(AEFD\) là hình thoi.
d)Diện tích tứ giác \(ABCD\) gấp hai lần diện tích tứ giác \(AEFD\).
Cho tam giác \(ABC\) vuông tại \(A.\) Gọi \(M\) là trung điểm của \(BC.\) Gọi \(H\) là hình chiếu của \(M\) trên \(AB.\) Lấy điểm \(D\) đối xứng với \(M\) qua \(H.\)
a)\(AM = BM = MC.\)
b)\(H\) là trung điểm của \(AB.\)
c)\(\widehat {DAB} > \widehat {BAM}.\)
d)Diện tích tứ giác \(AMBD\) bằng diện tích tam giác \(ABC\).
Cho hình bình hành \(ABCD\) có hai đường chéo cắt nhau tại \(O.\) Gọi \(M,\;N\) lần lượt là trung điểm của \(OB,\;OD.\)
a)\(OM = ON.\)
b)Tứ giác \(AMCN\) là hình bình hành.
c)\(AN > MC.\)
d)\(\widehat {DAN} = \widehat {MCB}.\)
Một hình thoi có chu vi bằng 36 cm thì độ dài cạnh của nó bằng bao nhiêu centimet?
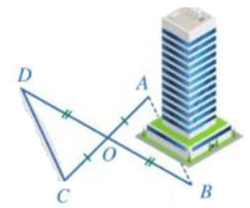
Để đo khoảng cách giữa hai vị trí \(A,\;B\) ở hai phía của một tòa nhà mà không thể đo được trực tiếp, người ta làm như sau: Chọn các vị trí \(O,\;C,\;D\) sao cho \(O\) không thuộc đường thẳng \(AB\) và khoảng cách \(CD\) là đo được và \(O\) là trung điểm của \(AC\) và \(BD.\) Người ta đo được \(CD = 150\;{\rm{m}}{\rm{.}}\) Độ dài \(AB\) bằng bao nhiêu \({\rm{m?}}\)
Một hình thoi có độ dài hai đường chéo là 12 cm và 16 cm. Tính độ dài cạnh của hình thoi đó. (Đơn vị: cm).
Cho hình thoi \(ABCD\) có chu vi bằng \(24{\rm{ cm,}}\) đường cao \(AH\) bằng \(3{\rm{ cm}}{\rm{.}}\) Hỏi số đo của \(\widehat {DCA}\) bằng bao nhiêu độ?
Tính diện tích hình bình hành \(ABCD\) có đường chéo \(AC\) vuông góc với cạnh \(AD.\) Biết rằng \(AC = 12\;{\rm{cm,}}\;AD = 9\;{\rm{cm}}{\rm{.}}\) (Đơn vị: \({\rm{c}}{{\rm{m}}^2}\)).