20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 3. Các trường hợp đồng dạng của hai tam giác vuông (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Điều kiện nào dưới đây không chứng tỏ hai tam giác vuông đồng dạng?
Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia.
Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.
Cạnh góc vuông và cạnh huyền của tam giác vuông này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác vuông.
Cạnh huyền của tam giác này bằng cạnh huyền của tam giác kia.
Cho \(\Delta ABC\) vuông tại \(A,\;\Delta MNP\)vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}.\)Khi đó:
Cho \(\Delta ABC\) vuông tại \(A\) và \(\Delta MNP\) vuông tại \(P.\) Để thì cần thêm điều kiện
\(\widehat A = \widehat M.\)
\(\widehat B = \widehat N.\)
\(\widehat A = \widehat N.\)
\(\widehat B = \widehat M.\)
Cho hình vẽ sau:
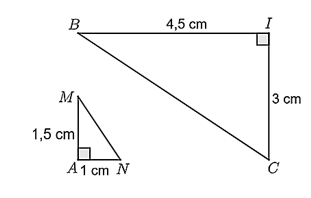
\(\widehat M = \frac{3}{4}\widehat B.\)
\(\widehat M = \frac{2}{3}\widehat B.\)
\(\widehat M = \widehat C.\)
\(\widehat M = \widehat B.\)
Nếu \(\Delta ABC\) và \(\Delta HIK\) có \(\widehat B = \widehat K,\;\,\widehat A = \widehat H = 90^\circ \) thì
Cho hình vẽ:
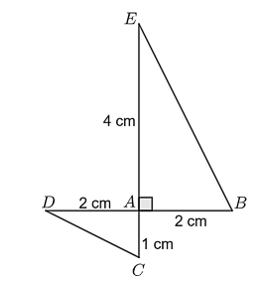
Khi đó:
Cho hình vẽ:
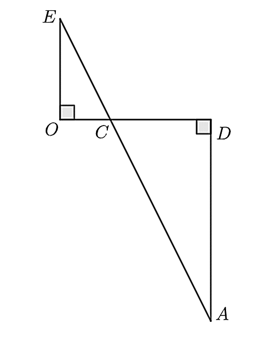
Khi đó:
Cho hình vẽ:
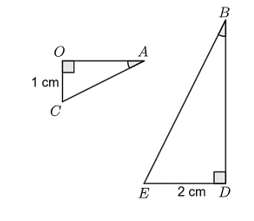
Khi đó:
\(BD = 1,5OA.\)
\(BD = 3OA.\)
\(BD = 2,5OA.\)
\(BD = 2OA.\)
Cho \(\Delta ABC\) vuông tại \(A.\) Lấy hai điểm \(M,\;\,N\) lần lượt thuộc các cạnh \(AB,\;\,AC\) sao cho \(AB = 3AN,\;\,BC = 3MN.\) Khi đó:
\(\widehat {AMN} = \widehat {ANM}.\)
\(\widehat {AMN} = \widehat C.\)
\(\widehat {AMN} = \widehat B.\)
\(\widehat {ANM} = \widehat C.\)
Chiều cao của ngọn tháp trong hình vẽ dưới đây bằng
\(20\;{\rm{m}}{\rm{.}}\)
\(25\;{\rm{m}}{\rm{.}}\)
\(30\;\,{\rm{m}}{\rm{.}}\)
\(16\;{\rm{m}}{\rm{.}}\)
Cho hình vẽ:
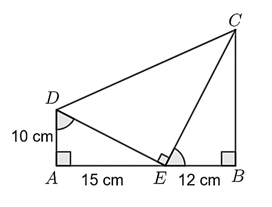
Khi đó:
\(\frac{{DE}}{{EC}} = \frac{{AE}}{{CB}} = \frac{2}{3}.\)
\(BC > 15\;{\rm{cm}}{\rm{.}}\)
Diện tích tứ giác \(ADCB\) lớn hơn \(200\;\,{\rm{c}}{{\rm{m}}^2}.\)
Cho hình vẽ:
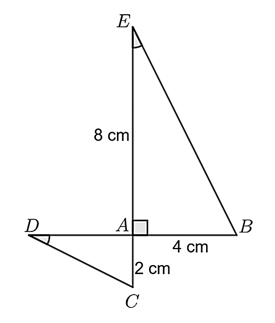
Khi đó:
\(EB > 10\;{\rm{cm}}{\rm{.}}\)
\(EB = 2DC.\)
Chu vi \(\Delta ADC\) lớn hơn \(15\;{\rm{cm}}{\rm{.}}\)
Một cột đèn cao \(3,5\;{\rm{m}}\) có bóng trên mặt đất dài \(2\;{\rm{m}}{\rm{.}}\) Gần đó có một tòa nhà cao tầng có bóng trên mặt đất là \(40\;\,{\rm{m}}\) và mỗi tầng của tòa nhà cao \(3,5\;\,{\rm{m}}{\rm{.}}\) (như hình vẽ)
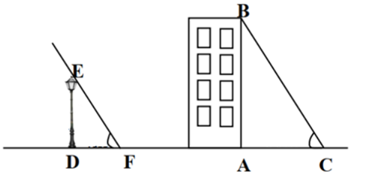
\(\frac{{AB}}{{AC}} = \frac{{DF}}{{DE}}.\)
Tòa nhà cao hơn \(80\;\,{\rm{m}}{\rm{.}}\)
Tòa nhà có nhiều hơn 20 tầng.
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH.\) Gọi \(M,\;\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\;\,AC.\)
\(A{H^2} = AN \cdot AC.\)
\(AM \cdot AB > AN \cdot AC.\)
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AE\;\,\left( {E \in BC} \right).\) Biết rằng \(AB = 40\;{\rm{cm,}}\;\,BC = 50\;{\rm{cm}}{\rm{.}}\)
\(BE = 32\;\,{\rm{cm}}.\)
\(AE > 30\;\,{\rm{cm}}{\rm{.}}\)
Cho tam giác \(ABC\) vuông tại \(A\;\,\left( {AB < AC} \right)\) có \(AM\;\,\left( {M \in BC} \right)\) là đường phân giác của tam giác đó. Kẻ đường thẳng vuông góc với \(BC\) tại \(M\) cắt \(AC\) tại \(N.\) Biết rằng \(MN = 5\;\,{\rm{m,}}\) tính độ dài đoạn thẳng \(MB.\) (Đơn vị: \({\rm{m}}\)).
Cho \(\Delta ABC\) vuông tại \(A,\;\,\Delta MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = 5.\) Hỏi độ dài \(BC\) gấp bao nhiêu lần độ dài \(NP?\)
Cho hình vẽ, biết \(NC = 1,5\,\,{\rm{cm, }}AN = 2\,\,{\rm{cm}}{\rm{.}}\)
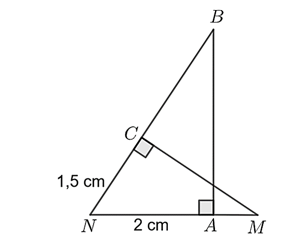
Khi đó, \(NM = ...NB.\) Tìm số thích hợp điền vào “…” để được đáp án đúng. (Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ:
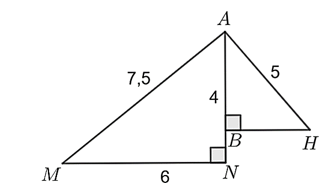
Đơn vị đo độ dài là \({\rm{cm}}{\rm{.}}\) Hỏi \(\widehat {MAH}\) có số đo bằng bao nhiêu độ?
Để đo chiều cao của một cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt của người quan sát nhìn thẳng vào gương, người quan sát di chuyển sao cho thấy được đỉnh ngọn đèn trong tấm gương và \(\widehat {ABC} = \widehat {A'BC'}.\) Cho chiều cao tính từ mắt của người quan sát đến mặt đất là \(AC = 1,5\;\,{\rm{m;}}\) khoảng cách từ gương đến chân người là \(BC = 0,75\;\,{\rm{m;}}\) khoảng cách từ gương đến chân cột đèn là \(BC' = 1,4\;{\rm{m}}{\rm{.}}\) Hỏi chiều cao của cột đèn là bao nhiêu mét? (Kết quả ghi dưới dạng số thập phân)