20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 2. Tọa độ của một điểm và đồ thị của hàm số (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho mặt phẳng \(Oxy\), trục \(Ox\) nằm ngang gọi là
trục tung.
trục hoành.
trục tọa độ.
\(Ox\)Tất cả đều sai.
Cho mặt phẳng \(Oxy\), trục \(Oy\) nằm dọc gọi là
trục tung.
trục hoành.
trục tọa độ.
Tất cả đều sai.
Trong mặt phẳng \(Oxy\), điểm \(O\) gọi là
tâm.
gốc chung.
gốc tọa độ.
gốc vuông.
Khẳng định nào sau đây là sai?
Một điểm mà nằm trên trục hoành thì tung độ bằng 0.
Trong mặt phẳng \(Oxy\) thì điểm \(M\left( {2;\,\,8} \right)\) có hoành độ bằng 8.
Trong mặt phẳng \(Oxy\) thì điểm \(N\left( {0;\,\, - 1} \right)\) nằm trên trục tung.
Một điểm mà nằm trên trụ tung thì hoành độ bằng 0.
Điểm nào dưới đây thuộc trục hoành?
\(A\left( {0;\;\,1} \right).\)
\(B\left( {0;\; - 1} \right).\)
\(C\left( {1;\;\,0} \right).\)
\(D\left( {1;\;\,1} \right).\)
Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(M\left( {1;\;\,3} \right).\) Khi đó:
Hoành độ của điểm \(M\) bằng 3.
Hoành độ của điểm \(M\) bằng \( - 3.\)
Tung độ của điểm \(M\) bằng 1.
Tung độ của điểm \(M\) bằng 3.
Cho đồ thị hàm số \(y = 2x + 4\) là đường thẳng màu xanh như hình vẽ:
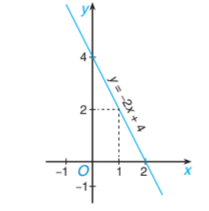
Điểm nào dưới đây thuộc đồ thị hàm số \(y = 2x + 4?\)
\(A\left( {1;\;2} \right).\)
\(B\left( {2;\;\,1} \right).\)
\(O\left( {0;\;\,0} \right).\)
\(M\left( {0;\;\,2} \right).\)
Trên mặt phẳng tọa độ \[Oxy,\] cho hai điểm \(A\) và \(B\) như hình vẽ:
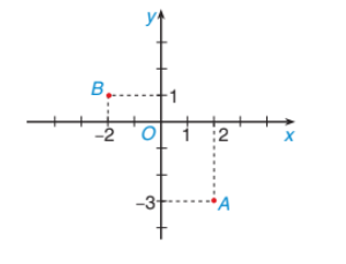
Khi đó:
Điểm \(A\) có hoành độ bằng \( - 3.\)
Điểm \(B\) có hoành độ bằng \( - 2.\)
Tung độ của điểm \(A\) lớn hơn 0.
Tung độ của điểm \(B\) nhỏ hơn 0.
Điểm nào dưới đây thuộc đồ thị của hàm số \(y = - {x^2} + 4?\)
\(A\left( {0;\;\,1} \right).\)
\(B\left( {0;\;\,2} \right).\)
\(C\left( {0;\;\,3} \right).\)
\(D\left( {0;\;\,4} \right).\)
Chọn khẳng định đúng trong các khẳng định sau:
Những điểm có hoành độ âm và tung độ dương thuộc góc phần tư thứ \(III.\)
Những điểm có hoành độ âm và tung độ âm thuộc góc phần tư thứ \(III.\)
Những điểm có hoành độ dương và tung độ dương thuộc góc phần tư thứ \(III.\)
Những điểm có hoành độ dương và tung độ âm thuộc góc phần tư thứ \(III.\)
Cho hệ trục tọa độ \(Oxy\) biểu diễn các điểm như sau:
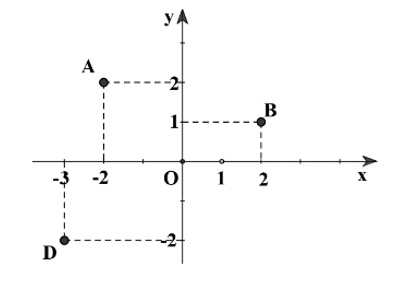
Tọa độ của điểm \(A\) là \(\left( { - 2;\,\,2} \right).\)
Cả ba điểm \(A;\,B;\,D\) đều có tung độ âm.
Không có điểm nào được biểu diễn ở góc phần tư thứ IV.
Điểm đối xứng với \(B\) qua trục hoành là \(B'\left( {2; - 1} \right)\).
Cho các điểm \(A;\,B;\,C;\,H\) được biểu diễn trên trục tọa độ \(Oxy\) như sau:
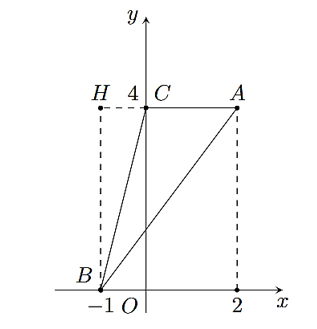
Điểm \(C\) nằm trên trục hoành.
Tọa độ của điểm \(H\) là \(\left( {4; - 1} \right)\).
Đường cao của tam giác \(ABC\) là \(HB = 4.\)
Diện tích tam giác \(ABC\) lớn hơn 4.
Cho bốn điểm \(A,\;\,B,\;\,C,\;\,D\) được biểu diễn trong mặt phẳng tọa độ như hình vẽ:
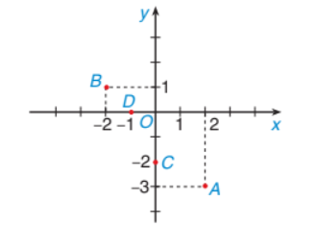
Điểm \(A\) có hoành độ bằng 2.
Hoành độ của điểm \(D\) là số dương.
Điểm \(B\) có hoành độ lớn hơn hoành độ của điểm \(C.\)
Tổng các hoành độ của bốn điểm \(A,\;\,B,\;\,C,\;\,D\) nhỏ hơn 5.
Cho hệ trục tọa độ \(Oxy\) biểu diễn các điểm như hình dưới đây:
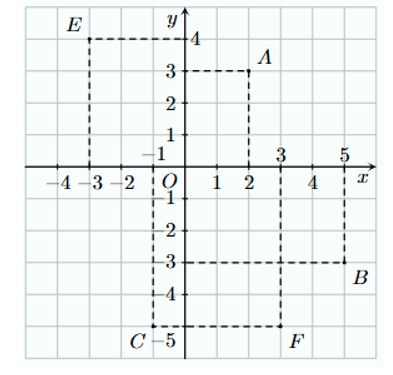
Điểm \(A\) có tọa độ \(A\left( {3;\,3} \right)\).
Điểm \(C\) có tọa độ \(C\left( { - 1;\, - 5} \right)\)
Có hai điểm được biểu diễn trong góc phần tư thứ I.
Điểm \(E\) và \(F\) đối xứng nhau qua gốc tọa độ.
Hình sau là đồ thị của hàm số mô tả nhiệt độ \(T\left( {^\circ C} \right)\) tại các thời điểm \(t\) (giờ) của một thành phố ở châu Âu từ giữa trưa đến 6 giờ tối.
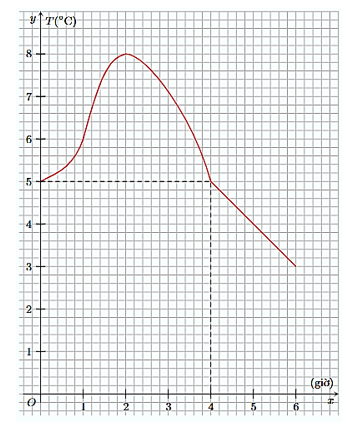
Khi đó,
\(T\left( 4 \right) = 5\).
Nhiệt độ lúc 1 giờ ở thành phố là \(6^\circ C.\)
\(T\left( t \right) = 5\) thì \(t = 0\) hoặc \(t = 4.\)
Trong khoảng thời gian từ 4 giờ đến 6 giờ thì nhiệt độ ở thành phố thấp hơn \(5^\circ C.\)
Cho hàm số \(y = f\left( x \right) = - mx + 4.\) Tìm giá trị của \(m\) để đồ thị hàm số đã cho đi qua điểm \(A\left( { - 1;\,\, - 1} \right)\).
Cho các điểm \(A\left( {0;\;\, - 4} \right);\;\,B\left( {4;\;\,0} \right);\;\,C\left( {1;\;\, - 2} \right);\;\,D\left( { - 2;\;\,1} \right).\)
Có bao nhiêu điểm trong các điểm đã cho thuộc đồ thị hàm số \(y = 2{x^2} - 4?\)
Cho các điểm có tọa độ như sau: \(A\left( {2;\,\,3} \right),\,B\left( {5;\, - 3} \right),\,C\left( { - 1;\, - 5} \right),\,E\left( { - 3;\,4} \right),F\left( {3;\, - 5} \right)\). Hỏi trong các điểm đã cho, có bao nhiêu điểm thuộc góc phần tư thứ I?
Biết rằng đồ thị của hàm số \(f\left( x \right) = a{x^2} - 4\) đi qua điểm \(I\left( {2;0} \right)\). Hỏi giá trị của \(a\) bằng bao nhiêu?
Biết rằng đồ thị của hàm số \(f\left( x \right) = a{x^2} + b\) đi qua hai điểm \(A\left( {0;\;\,1} \right)\) và \(B\left( {2;\;9} \right).\) Tính \(a + b.\)
