20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 2. Đường trung bình của tam giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Đoạn thẳng nối trung điểm hai cạnh của tam giác là:
Đường trung bình của tam giác.
Đường trung trực của tam giác.
Đường trung tuyến của tam giác.
Đường cao của tam giác.
Cho \(\Delta ABC\) có \(D,\;E\) lần lượt là trung điểm của \(AB,\;AC.\) Khi đó:
\(DE = \frac{1}{3}BC.\)
\(DE = \frac{1}{2}BC.\)
\(DE = \frac{2}{3}BC.\)
\(DE = \frac{3}{4}BC.\)
Cho hình vẽ:
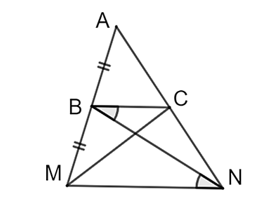
Khi đó:
\(MC\) là đường trung bình của \(\Delta AMN.\)
\(MC\) là đường trung trực của \(\Delta AMN.\)
\(MC\) là đường phân giác của \(\Delta AMN.\)
\(MC\) là đường trung tuyến của \(\Delta AMN.\)
Cho \(\Delta ABC\) có \(M\) là trung điểm của \(AB,\;N\) là trung điểm của \(AC.\) Khi đó:
\(MN \bot BC.\)
\(MN\;{\rm{//}}\;BC.\)
\(MN\) là đường trung tuyến của \(\Delta ABC.\)
\(MN\) là đường trung trực của \(\Delta ABC.\)
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(AB,\) qua \(D\) kẻ đường thẳng song song với \(BC\) cắt cạnh \(AC\) tại \(E.\) Khi đó:
\(\frac{{AC}}{{AE}} = \frac{4}{3}.\)
\(\frac{{AC}}{{AE}} = 3.\)
\(\frac{{AC}}{{AE}} = 2.\)
\(\frac{{AC}}{{AE}} = \frac{5}{3}.\)
Cho hình vẽ:
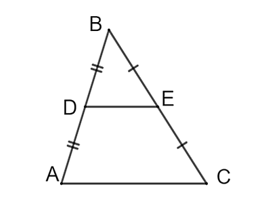
Khi đó:
\(\widehat C = \widehat {BED}.\)
\(\widehat C = \frac{2}{3}\widehat {BED}.\)
\(\widehat C = \frac{3}{4}\widehat {BED}.\)
\(\widehat C = \frac{1}{2}\widehat {BED}.\)
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Gọi \(E\) là trung điểm của \(BC.\) Khi đó:
\(OE\;{\rm{//}}\;DC.\)
\(CD = 2OE.\)
Cả A, B đều sai.
Cả A, B đều đúng.
Cho \(\Delta ABC.\) Lấy điểm \(I\) đối xứng với \(A\) qua \(B\) và điểm \(K\) đối xứng với \(A\) qua \(C\) thì:
\(BC = IK.\)
\(BC = \frac{1}{2}IK.\)
\(BC = 2IK.\)
\(BC = \frac{2}{3}IK.\)
Cho hình chữ nhật \(ABCD\) có \(AD = 4\;{\rm{cm}},\;E\) là giao điểm của hai đường chéo. Qua \(E\) vẽ đường thẳng song song với \(BC\) cắt \(AB\) tại \(F.\) Khi đó:
\(EF = 1\;{\rm{cm}}{\rm{.}}\)
\(EF = 2\;{\rm{cm}}{\rm{.}}\)
\(EF = 2,5\;{\rm{cm}}{\rm{.}}\)
\(EF = 3\;{\rm{cm}}{\rm{.}}\)
Giữa hai điểm \(B\) và \(C\) có một hồ sâu (như hình vẽ). Biết khoảng cách giữa hai điểm \(D\) và \(E\) đo được là \(110\;{\rm{m}}{\rm{.}}\) Khi đó, khoảng cách giữa hai điểm \(B\) và \(C\) là:
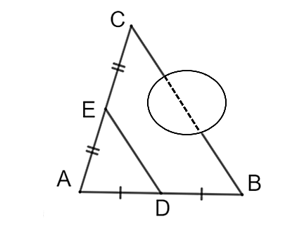
\(150\;{\rm{m}}{\rm{.}}\)
\(200\;{\rm{m}}{\rm{.}}\)
\(220\;{\rm{m}}{\rm{.}}\)
\(210\;{\rm{m}}{\rm{.}}\)
Cho hình vẽ:
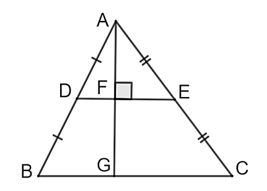
Biết rằng \(AF = 8\;{\rm{cm}},\;FE = 6\;{\rm{cm}}.\)
\(DE\;{\rm{//}}\;BC.\)
\(F\) là trung điểm của \(AG.\)
\(GC = 16\;{\rm{cm}}{\rm{.}}\)
Diện tích \(\Delta AGC\) bằng \(48\;{\rm{c}}{{\rm{m}}^2}.\)
Cho hình vẽ:
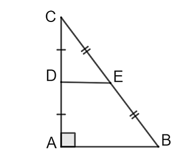
\(DE\) là đường trung tuyến của tam giác \(ABC.\)
\(DE = \frac{1}{2}AB.\)
Diện tích \(\Delta CDE\) là: \({S_{\Delta CDE}} = \frac{1}{2}AC \cdot AB.\)
Diện tích tam giác \(ABC\) gấp bốn lần diện tích tam giác \(CDE.\)
Cho tứ giác \(ABCD\) có \(M,\;E,\;F\) lần lượt là trung điểm của \(DB,\;AD\) và \(BC.\)
\(EM\) là đường trung bình của \(\Delta ABD.\)
\(MF = \frac{1}{3}DC.\)
\(ME + MF \ge EF.\)
\(EF \ge \frac{{AB + CD}}{2}.\)
Cho \(\Delta ABC\) nhọn. Gọi \(M\) là trung điểm của \(BC.\) Gọi \(I\) là trung điểm của \(AM\) và \(E\) là giao điểm của \(CI\) và \(AB.\) Từ \(M\) kẻ đường thẳng song song với \(CE\) cắt \(AB\) tại \(F.\)
\(BE = 2FE.\)
\(AF = \frac{2}{3}AB.\)
\(MF = 3IE.\)
CI = EC
Cho hình thang \(ABCD\;\left( {AB\;{\rm{//}}\;CD} \right)\) có \(E,\;F\) lần lượt là trung điểm của \(AD,\;BC.\) Gọi \(K\) là giao điểm của \(AF\) và \(CD.\)
\(AB > CK.\)
\(EF\;{\rm{//}}\;AB\;{\rm{//}}\;CD.\)
\(EF = \frac{1}{2}DK.\)
\(EF = \frac{{AB + CD}}{3}.\)
Cho tam giác \(ABC\) có \(M,\;N\) lần lượt là trung điểm của \(AC,\;BC.\) Gọi \(I\) là giao điểm của \(AN\) và \(BM.\) Trên tia đối của tia \(MB\) lấy điểm \(F\) sao cho \(M\) là trung điểm của \(FI.\) Trên tia đối của tia \(NA\) lấy điểm \(E\) sao cho \(N\) là trung điểm của \(EI.\) Khi đó, \(\widehat F = ...\widehat {ABM}.\) Tìm số thích hợp điền vào dấu “…”.
Cho tam giác \(ABC\) có \(BC = 12\;{\rm{cm}}{\rm{.}}\) Gọi \(M,\;N,\;E\) lần lượt là trung điểm của \(AB,\;AC,\;BC.\) Gọi \(I\) là giao điểm của \(AE\) và \(MN.\) Tính độ dài \(IN.\) (Đơn vị: \({\rm{cm}}\)).
Cho \(\Delta ABC\) có chu vi bằng \(40\;{\rm{cm}}{\rm{.}}\) Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC.\) Chu vi \(\Delta AMN\) bằng bao nhiêu \({\rm{cm}}?\)
Cho tam giác \(ABC\) có \(H\) là trung điểm \(BC.\) Qua \(H\) kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(K.\) Biết rằng \(AB + HK = 18\;{\rm{cm}}{\rm{.}}\) Hỏi độ dài đoạn thẳng \(HK\) bằng bao nhiêu \({\rm{cm?}}\)
Cho hình chữ nhật \(ABCD\) có \(AB = 15\;{\rm{cm}},\;CB = 20\;{\rm{cm}}.\) Gọi \(E,\;F,\;G,\;H\) lần lượt là trung điểm của \(AB,\;BC,\;CD,\;DA.\) Tính diện tích tứ giác \(EFGH.\) (đơn vị đo là \({\rm{c}}{{\rm{m}}^2}\)).
