20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Diện tích xung quanh của hình chóp tam giác đều biết độ dài đáy bằng 5 cm, chiều cao của tam giác mặt bên kẻ từ đỉnh của hình chóp tam giác đều bằng 6 cm là
\(45\,\,{\rm{cm}}.\)
\(90\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(15\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(45\,\,{\rm{c}}{{\rm{m}}^2}.\)
Thể tích của hình chóp là
tích nửa chu vi đáy và đường cao của hình chóp.
tích nửa chu vi đáy và đường cao
một phần ba tích diện tích đáy và chiều cao.
một phần b tích diện tích đáy và trung đoạn.
Một hình chóp tứ giác đều có diện tích đáy bằng \(30\,\;{\rm{c}}{{\rm{m}}^2}\) và chiều cao bằng \(4\;\,{\rm{cm}}{\rm{.}}\) Thể tích hình chóp tứ giác đều đó bằng
\(120\,\;{\rm{c}}{{\rm{m}}^2}.\)
\(120\;\,{\rm{c}}{{\rm{m}}^3}.\)
\(40\;\,{\rm{c}}{{\rm{m}}^3}.\)
\(40\;\,{\rm{c}}{{\rm{m}}^2}.\)
Một hình chóp tam giác đều có chu vi đáy bằng \(40\;\,{\rm{cm}}\) và độ dài trung đoạn bằng \(6\;\,{\rm{cm}}{\rm{.}}\) Diện tích xung quanh của hình chóp tam giác đều đó bằng
\(120\;\,{\rm{c}}{{\rm{m}}^2}.\)
\(120\,\;{\rm{c}}{{\rm{m}}^3}.\)
\(40\;\,{\rm{c}}{{\rm{m}}^3}.\)
\(40\;\,{\rm{c}}{{\rm{m}}^2}.\)
Thể tích khối chóp tứ giác đều có cạnh đáy dài \(7\,{\rm{cm}}\) và độ dài chiều cao \(9\,{\rm{cm}}\) là
\(63\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(147\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(72\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(441\,\,{\rm{c}}{{\rm{m}}^3}.\)
Cho hình chóp tứ giác đều có thể tích bằng \(50\,\,{\rm{c}}{{\rm{m}}^3}\) chiều cao là \(6\,\,{\rm{cm}}{\rm{.}}\) Độ dài cạnh đáy của hình chóp đó là
50 cm.
5 cm.
25 cm.
\(12,5\,\,{\rm{cm}}.\)
Cho hình chóp tam giác đều có các mặt bên là các tam giác cân có diện tích bằng \(10\,\,{\rm{c}}{{\rm{m}}^2}.\) Diện tích xung quanh của hình chóp đó là
\(10\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(20\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(40\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(30\,\,{\rm{c}}{{\rm{m}}^2}.\)
Cho hình chóp tứ giác đều có thể tích bằng \(32\,\,{\rm{c}}{{\rm{m}}^3},\) chiều cao hình chóp đó bằng \(6\,\,{\rm{cm,}}\) chiều cao mặt bên bằng \(10\,\,{\rm{cm}}{\rm{.}}\) Tính diện tích xung quanh hình chóp đó.
\(40\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(50\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(60\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(80\,\,{\rm{c}}{{\rm{m}}^2}.\)
Cho hình chóp tứ giác đều có chu vi đáy là 20 cm, chiều cao có số đo gấp 3 lần cạnh đáy. Thể tích của khối chóp đó là
\(80\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(125\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(25\,\,{\rm{c}}{{\rm{m}}^3}.\)
\(375\,\,{\rm{c}}{{\rm{m}}^3}.\)
Diện tích xung quanh của hình chóp tam giác đều có cạnh đáy bằng 10 cm và độ dài chiều cao mặt bên là 12 cm là
\(240\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(120\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(169\,\,{\rm{c}}{{\rm{m}}^2}.\)
\(180\,\,{\rm{c}}{{\rm{m}}^2}.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Sau khi cắt và gấp miếng bìa như hình dưới đây ta được một hình chóp tứ giác đều.
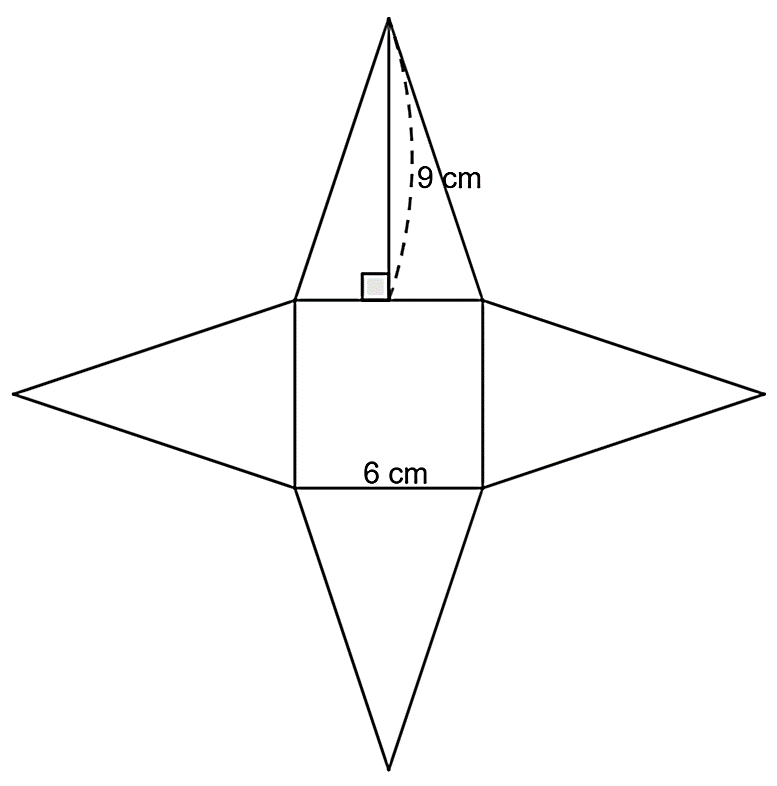
a) Trung đoạn của hình chóp tứ giác đều có độ dài bằng \(6\;\,{\rm{cm}}{\rm{.}}\)
b) Chu vi đáy của hình chóp tứ giác đều bằng \(36\;\,{\rm{cm}}{\rm{.}}\)
c) Diện tích xung quanh của hình chóp tứ giác đều bằng \(108\;\,{\rm{c}}{{\rm{m}}^2}.\)
d) Diện tích toàn phần của hình chóp tứ giác đều bằng \(144\;\,{\rm{c}}{{\rm{m}}^2}.\)
Cho hình chóp tứ giác đều \(S.ABCD\) có \(SO\) là đường phân giác trong tam giác \(SAC.\) Biết rằng \(BD = 6\,\;{\rm{cm,}}\;\,SO = \frac{3}{2}BD.\)
a)Tam giác \(SAC\) là tam giác cân tại \(S.\)
b)\(O\) là giao điểm của \(AC\) và \(BD.\)
c)\(SO\) là đường cao của hình chóp \(S.ABCD.\)
d)Thể tích của hình chóp \(S.ABCD\) bằng \(48\;\,{\rm{c}}{{\rm{m}}^3}.\)
Một khối gỗ (như hình vẽ) gồm đế là hình lập phương có cạnh \(18\;\,{\rm{cm}}\) và phần trên là một hình chóp tứ giác đều:
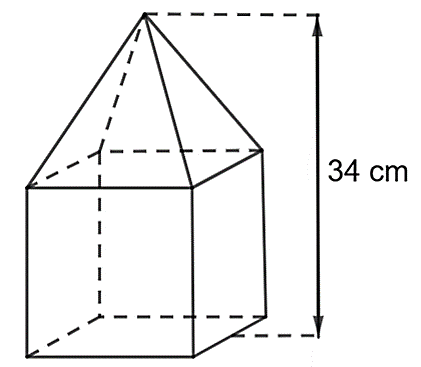
a)Chiều cao của hình chóp tứ giác đều bằng \(16\;\,{\rm{cm}}{\rm{.}}\)
b)Thể tích đế khối gỗ là \(5\;\,832\;\,{\rm{c}}{{\rm{m}}^3}.\)
c)Thể tích phần trên của khối gỗ là \(1\;\,728\;\;{\rm{c}}{{\rm{m}}^3}.\)
d)Thể tích của khối gỗ nhỏ hơn \(7\;\,{\rm{d}}{{\rm{m}}^3}.\)
Từ một khúc gỗ hình lập phương cạnh \(45\;\,{\rm{cm}}\) (hình vẽ), người ta cắt đi một phần gỗ để được phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh \(45\;\,{\rm{cm}}\) và chiều cao của hình chóp cũng bằng \(45\;\,{\rm{cm}}{\rm{.}}\)
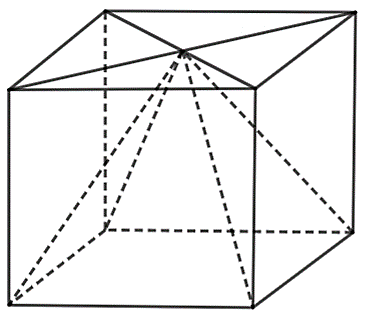
a)Thể tích khúc gỗ hình lập phương bằng \(91\;\,125\;\,{\rm{c}}{{\rm{m}}^3}.\)
b)Thể tích khối gỗ còn lại bằng \(30\;375\;\,{\rm{c}}{{\rm{m}}^3}.\)
c)Thể tích khối gỗ bị cắt đi lớn hơn \(60\;000\;\,{\rm{c}}{{\rm{m}}^3}.\)
d)Tỉ số giữa thể tích phần khối gỗ còn lại và thể tích phần khối gỗ bị cắt đi bằng \(\frac{2}{3}.\)
Cho hình chóp tam giác đều \(S.ABC\) có \(SI\;\,\left( {I \in BC} \right)\) là trung đoạn của hình chóp đó. Trên đoạn thẳng \(AI\) lấy điểm \(O\) sao cho \(OI = \frac{1}{3}AI.\) Biết rằng \(SO = 9\;{\rm{cm}}\) và diện tích tam giác \(ABC\) bằng \(30\;{\rm{c}}{{\rm{m}}^2}.\) Khi đó:
a)\(I\) là trung điểm của \(BC.\)
b)\(O\) là trọng tâm của tam giác \(ABC.\)
c)\(SO\) là đường cao của hình chóp tam giác đều \(S.ABC.\)
d)Thể tích của hình chóp tam giác đều \(S.ABC\) bằng \(60\;{\rm{c}}{{\rm{m}}^3}.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Một hộp quà lưu niệm có dạng hình chóp tứ giác đều (hình vẽ) với độ dài cạnh đáy là \(10\;\,{\rm{cm}}\) và chiều cao \(15\;{\rm{cm}}{\rm{.}}\) Hỏi thể tích hộp quà lưu niệm đó bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}?\)

Một hình chóp tứ giác đều có thể tích bằng \(60\;\,{\rm{c}}{{\rm{m}}^3}\) và chiều cao của hình chóp đó bằng \(5\;\,{\rm{cm}}{\rm{.}}\) Hỏi độ dài cạnh đáy của hình chóp tứ giác đều đó bằng bao nhiêu \({\rm{cm?}}\)
Một đồ chơi có dạng hình chóp tam giác đều (hình vẽ). Độ dài cạnh đáy của hình chóp bằng \(10\,\;{\rm{cm}}{\rm{.}}\) Chiều cao kẻ đỉnh hình chóp tới cạnh đáy bằng \(12\;\,{\rm{cm}}{\rm{.}}\) Tính diện tích giấy để làm vỏ bọc ba mặt bên của món đồ chơi này (coi mép dán không đáng kể) (Đơn vị: \({\rm{c}}{{\rm{m}}^2}\)).

Một hình chóp tứ giác đều có thể tích là \({V_1}.\) Nếu giữ nguyên chiều cao của hình chóp đó và tăng độ dài cạnh đáy lên 2 lần thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)
Một hình chóp tứ giác đều \(S.ABCD\) có thể tích bằng \(200\;\,{\rm{c}}{{\rm{m}}^3}.\) Gọi \(M,\;\,N,\;\,P,\;\,Q\) lần lượt là trung điểm của \(AB,\;\,BC,\;\,CD,\;\,DA.\) Biết rằng \(SO\) là đường cao của hai hình chóp \(S.ABCD\)và \(S.MNPQ.\) Tính thể tích của hình chóp \(S.MNPQ\) (Đơn vị: \({\rm{c}}{{\rm{m}}^3}\)).

