20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 2. Các trường hợp đồng dạng của hai tam giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Chọn khẳng định đúng.
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai tam giác đó có hai góc bằng nhau thì hai tam giác đó đồng dạng với nhau.
Cho \(\Delta HIK\) và \(\Delta MNP\) có \(\widehat H = \widehat M;\;\,\widehat K = \widehat N.\) Khi đó:
Cho \(\Delta ABC\) và \(\Delta MNP\) có \(\frac{{AB}}{{MN}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{PN}}\) thì:
Cho \(\Delta ABC\) và \(\Delta MNP\) có \(AB = 2MN;\;\,MP = \frac{1}{2}AC;\;\,BC = 2NP\) thì
Cho hình vẽ:
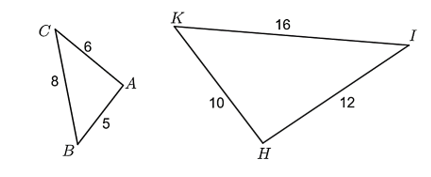
Khi đó:
Cho hình vẽ:
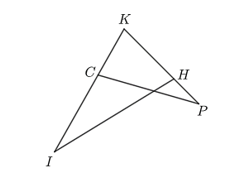
Biết rằng \(IK = 4\;{\rm{cm;}}\;\,KP = 3\;{\rm{cm}};\;\,CK = 1,5\;{\rm{cm}};\;\,KH = 2\;{\rm{cm}}.\) Khi đó:
Nếu \(\Delta ABC\) và \(\Delta HIK\) có \(\frac{{AB}}{{HI}} = \frac{{AC}}{{HK}},\;\,\widehat A = \widehat H\) thì
Cho hình vẽ:
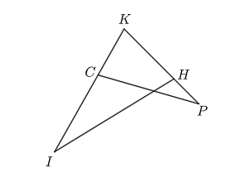
Biết rằng đơn vị đo trên các cạnh là mét, khi đó:
\(\widehat {ADE} = \frac{2}{3}\widehat C.\)
\(\widehat {ADE} = \frac{3}{4}\widehat C.\)
\(\widehat {ADE} = \widehat C.\)
\(\widehat C = \frac{3}{4}\widehat {ADE}.\)
Cho \(\Delta AIC\) có \(AI = 12\;\,{\rm{cm;}}\;\,CI = 18\;\,{\rm{cm}}{\rm{.}}\) Trên tia đối của tia \(IA\) lấy điểm \(B\) sao cho \(IB = 15\;\,{\rm{cm,}}\) trên tia đối của tia \(IC\) lấy điểm \(D\) sao cho \(ID = 10\;\,{\rm{cm}}{\rm{.}}\) Khi đó:
\(\widehat C = \widehat B.\)
\(\widehat C = \frac{2}{3}\widehat B.\)
\(\widehat B = \frac{2}{3}\widehat C.\)
\(\widehat B = \frac{3}{4}\widehat C.\)
Cho hình vẽ:
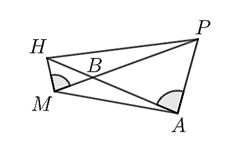
Khi đó:
\(\frac{{HB}}{{AB}} = \frac{{MB}}{{PB}}.\)
\(\frac{{HB}}{{PB}} = \frac{{AB}}{{MB}}.\)
\(\frac{{HB}}{{PB}} = \frac{{MB}}{{AB}}.\)
\(\frac{{HB}}{{MB}} = \frac{{AB}}{{PB}}.\)
Cho \(\Delta ABC\) và các điểm \(M,\;\,N\) lần lượt thuộc các cạnh \(AB,\;\,AC\) sao cho \(\widehat {ANM} = \widehat {ABC}.\)
\(\frac{{AN}}{{AM}} > \frac{{AB}}{{AC}}.\)
\(\widehat {OBM} = \widehat {OCN}.\)
Cho hình vẽ:
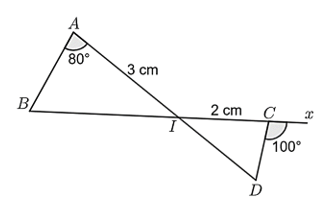
Khi đó:
\(\widehat {ICD} = 80^\circ .\)
\(\frac{{AB}}{{CD}} = \frac{4}{3}.\)
Chu vi tam giác \(\Delta AIB\) bằng \(1,5\) lần chu vi tam giác \(\Delta ICD.\)
Cho tứ giác \(ABCD\) có \(AB = 4\;\,{\rm{cm,}}\;\,AD = 6\;\,{\rm{cm,}}\;\,BD = 8\;\,{\rm{cm,}}\;\,BC = 12\;\,{\rm{cm,}}\;\,CD = 16\;\,{\rm{cm}}{\rm{.}}\)
\(\frac{{AB}}{{BD}} > \frac{{AD}}{{BC}} = \frac{{BD}}{{DC}}.\)
với tỉ số đồng dạng là \(0,5.\)
\(\widehat {ABD} > \widehat {BDC}.\)
Tứ giác \(ABCD\) là hình thang có \(BC\) là đáy lớn.
Cho hình thang \(ABCD\;\,\left( {AB\;{\rm{//}}\;CD} \right)\) như hình vẽ:
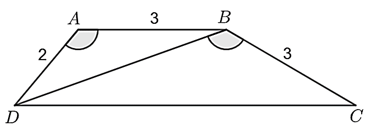
Biết rằng đơn vị đo độ dài các cạnh là mét. Khi đó:
\(\widehat {ABD} > \widehat {BDC}.\)
\(\frac{{AB}}{{BD}} = \frac{{BD}}{{CD}} = \frac{2}{3}.\)
Chu vi hình thang \(ABCD\) lớn hơn \(15\;{\rm{cm}}{\rm{.}}\)
Cho \(\widehat {xOy},\) trên tia \(Ox\) lấy các điểm \(A,\;\,C;\) trên tia \(Oy\) lấy các điểm \(B,\;\,D\) sao cho \(OA \cdot OC = OB \cdot OD.\) Gọi \(E\) là giao điểm của \(AD\) và \(BC.\)
\(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}.\)
\(AE \cdot ED = CE \cdot EB.\)
Cho tam giác \(ABC\) có \(AB = 6\;\,{\rm{cm,}}\;\,AC = 7,5\;\,{\rm{cm}}{\rm{.}}\) Trên các cạnh \(AB,\;\,AC\) lần lượt lấy các điểm \(M,\;\,N\) sao cho \(AM = 5\;\,{\rm{cm,}}\;\,AN = 4\;\,{\rm{cm}}{\rm{.}}\) Khi đó, \(\widehat {AMN} = ...\widehat C.\)
Tìm số thích hợp để điền vào “…” để được đáp án đúng.
Cho tam giác \(ABC\) có \(AB = 2\;\,{\rm{cm,}}\;\,AC = 4\;\,{\rm{cm}}{\rm{.}}\) Trên cạnh \(AC\) lấy điểm \(D\) sao cho \(AD = 1\;\,{\rm{cm}}{\rm{.}}\) Hỏi độ dài đoạn thẳng \(BC\) gấp bao nhiêu lần độ dài đoạn thẳng \(BD?\)
Cho \(\Delta ABC\) và \(\Delta MNP\) có:
\(AB = 2\;\,{\rm{cm;}}\;\,AC = 4\;\,{\rm{cm;}}\;\,\widehat A = 50^\circ ;\;\,MN = 6\;\,{\rm{cm;}}\;\,MP = 12\;\,{\rm{cm;}}\;\,\widehat M = 50^\circ .\)
Tính tỉ số \(\frac{{BC}}{{NP}}.\) (Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ, biết \(EC = 4\,\,{\rm{cm}};\,\,\,AC = 8\,\,{\rm{cm}}{\rm{.}}\)
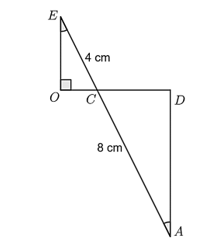
Hỏi diện tích \(\Delta ACD\) gấp bao nhiêu lần diện tích tích \(\Delta OCE?\)
Cho hình vẽ, biết: \(KC = 1,5\,\,{\rm{cm}};\,\,\,KI = 3\,\,{\rm{cm}}{\rm{.}}\)
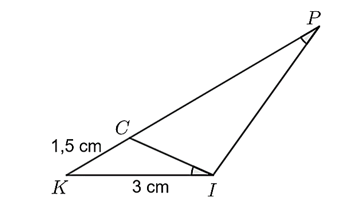
Hỏi độ dài \(CP\) bằng bao nhiêu centimet? (Kết quả ghi dưới dạng số thập phân)
