20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1. Mô tả xác suất bằng tỉ số (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Chọn đáp án sai.
Số kết quả thuận lợi của một biến cố có thể bằng tổng số kết quả có thể xảy ra của phép thử.
Số kết quả thuận lợi của một biến cố có thể nhỏ hơn tổng số kết quả có thể xảy ra của phép thử.
Số kết quả thuận lợi của một biến cố có thể bằng 0.
Số kết quả thuận lợi của một biến cố có thể lớn hơn tổng số kết quả có thể xảy ra của phép thử.
Một phép thử có tất cả các kết quả có khả năng quả xảy như nhau. Gọi tổng số kết quả có thể xảy ra của phép thử đó là \(n\) và \(n\left( A \right)\) là số kết quả thuận lợi của biến cố \(A\) thì xác suất của biến cố \(A\) bằng
\(\frac{n}{{n\left( A \right)}}.\)
\(\frac{{n\left( A \right)}}{n}.\)
\(n - n\left( A \right).\)
\(n + n\left( A \right).\)
Gieo một con xúc xắc một lần. Số chấm xuất hiện trên con xúc xắc là những số nào để số kết quả thuận lợi biến cố “Số chấm xuất hiện trên con xúc xắc là hợp số” khác 0?
\(1;\;4;\;6.\)
\(2;\;4;\;6.\)
\(4;\;\,6.\)
\(4;\;\,5;\;\,6.\)
Khi tính xác suất của biến cố, các kết quả có thể của phép thử cần có điều kiện gì?
Đồng khả năng.
Có thể đồng khả năng hoặc không cần đồng khả năng.
Không cần đồng khả năng.
Giống nhau.
Cho \(A\) và \(B\) là hai biến cố khác nhau. Biết rằng \(A\) và \(B\) là hai biến cố đồng khả năng. Gọi \(P\left( A \right),\;\,P\left( B \right)\) lần lượt là xác suất xảy ra của hai biến cố \(A\) và \(B.\) Khi đó:
\(P\left( A \right) < P\left( B \right).\)
\(P\left( A \right) > P\left( B \right).\)
\(P\left( A \right) = P\left( B \right).\)
\(P\left( A \right) \ne P\left( B \right).\)
Một hộp đựng 4 quả bóng màu vàng được đánh số \(1;\;\,2;\;\,3;\;\,4\) và 3 quả bóng tím được đánh số \(1;\;\,2;\;\,3.\) Lấy ngẫu nhiên đồng thời 2 quả bóng trong hộp. Tổng số kết quả thuận lợi của biến cố “2 quả bóng lấy được đều đánh số chẵn” là
4.
3.
5.
6.
Một tấm bìa hình tròn được chia thành 8 hình quạt bằng nhau và được đánh số từ 1 đến 8 (như hình vẽ). Xoay tấm bìa quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Xác suất của biến cố \(A:\) “Mũi tên chỉ vào ô ghi số lớn hơn 6” là
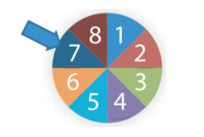
\(0,4.\)
\(0,25.\)
\(0,3.\)
\(0,2.\)
Gieo một con xúc xắc cân đối và đồng chất. Xác suất của biến cố \(M:\) “Gieo được mặt có số chấm là số chính phương” là
\(\frac{1}{6}.\)
\(\frac{1}{3}.\)
\(\frac{1}{4}.\)
\(\frac{1}{5}.\)
Một hộp đựng 4 quả bóng màu vàng được đánh số \(1;\;\,2;\;\,3;\;\,4\) và 3 quả bóng màu tím được đánh số \(1;\;\,2;\;\,3.\) Lấy ngẫu nhiên 1 quả bóng trong hộp. Xác suất của biến cố \(H:\) “Lấy được quả bóng được đánh số chẵn” là
\(\frac{5}{7}.\)
\(\frac{3}{7}.\)
\(\frac{4}{7}.\)
\(\frac{2}{7}.\)
Tỉ lệ thành viên nữ của một câu lạc bộ nhảy là \(75\% .\) Tổng số thành viên của câu lạc bộ đó là 40 người. Gặp ngẫu nhiên 1 thành viên trong câu lạc bộ đó, xác suất thành viên đó là nam bằng
\(0,6.\)
\(0,3.\)
\(0,5.\)
\(0,25.\)
Lớp 8A có 40 học sinh, trong đó số học sinh nữ chiếm \(25\% \) số học sinh của cả lớp. Cô giáo chọn ngẫu nhiên một bạn học sinh trong lớp để tham gia hoạt động bảo vệ môi trường của khối 8.
Xét các biến cố:
\(M:\) “Học sinh được chọn là học sinh nam”;
\(N:\) “Học sinh được chọn là học sinh nữ”.
Khi đó:
Số học sinh nam của lớp 8A là 30 học sinh.
Số kết quả có thể của hành động trên là 40.
Tổng số kết quả thuận lợi của biến cố \(M\) là 20.
Tổng số kết quả thuận lợi của biến cố \(N\) ít hơn tổng số kết quả thuận lợi của biến cố \(M.\)
Bạn Linh cố 16 tấm thẻ, mỗi tấm thẻ ghi một chữ cái trong từ “ENVIRONMENTALIST”. Bạn ấy rút ngẫu nhiên một tấm thẻ. Xét các biến cố:
\(M:\) “Rút được tấm thẻ ghi chữ E”;
\(N:\) “Rút được tấm thẻ ghi chữ T”;
\(Q:\) “Rút được tấm thẻ ghi chữ N”.
Khi đó,
Có 16 kết quả có thể đồng khả năng của hành động trên.
Xác suất của biến cố \(M\) bằng \(0,3.\)
Khả năng xảy ra biến cố \(M\) và biến cố \(N\) bằng nhau.
Trong ba biến cố trên, khả năng xảy ra biến cố \(Q\) là cao nhất.
Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 4, hộp thứ hai chứa các thẻ được đánh số từ 5 đến 8. Lấy ngẫu nhiên ở mỗi hộp 1 thẻ, ghép lại được thành một số có hai chữ số (số ở hộp thứ nhất đứng ở hàng chục).
Gọi \(A\) là biến cố: “Số được tạo thành là số chẵn”;
\(B\) là biến cố: “Số được tạo thành lớn hơn 40”;
\(C\) là biến cố: “Số được tạo thành là số chia hết cho 3”.
Có tất cả 20 kết quả có thể đồng khả năng của hành động trên.
Xác suất của biến cố \(A\) bằng \(0,5.\)
Xác suất của biến cố \(A\) lớn hơn xác suất của biến cố \(B.\)
Xác suất của biến cố \(A\) bằng tổng của xác suất biến cố \(B\) và xác suất của biến cố \(C.\)
Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 4, hộp thứ hai chứa các thẻ được đánh số từ 5 đến 8. Lấy ngẫu nhiên ở mỗi hộp 1 thẻ, ghép lại được thành một số có hai chữ số (số ở hộp thứ nhất đứng ở hàng chục). Cho các biến cố:
\(A\) là biến cố: “Số được tạo thành là số chẵn”;
\(B\) là biến cố: “Số được tạo thành nhỏ hơn 50”;
\(C\) là biến cố: “Số được tạo thành là số chia hết cho 5”.
Khi đó:
Có tất cả 20 kết quả có thể của hành động trên.
Có 8 kết quả thuận lợi của biến cố \(A.\)
Số kết quả thuận lợi của biến cố \(B\) bằng tổng số kết quả có thể của hành động trên.
Số kết quả thuận lợi của biến cố \(B\) nhỏ hơn tổng số kết quả thuận lợi của biến cố \(A\) và biến cố \(C.\)
Một túi đựng 5 viên bi được ghi số \(11;\;\,12;\;\,13;\;\,14;\;\,15.\) Bạn Ninh lấy ngẫu nhiên đồng thời hai viên bi từ trong hộp. Xét các biến cố:
\(E:\) “Tổng hai số ghi trên hai viên bi là một số lẻ”;
\(F:\) “Tổng hai số ghi trên hai viên bi là một số nguyên tố”.
\(G:\) “Tổng hai số ghi trên hai viên bi là một số lớn hơn 25”.
Có 12 kết quả đồng khả năng có thể của hành động trên.
Xác suất của biến cố \(E\) bằng \(0,25.\)
Xác suất xảy ra của biến cố \(E\) lớn hơn xác suất xảy ra của biến cố \(F.\)
Trong ba biến cố \(E,\;\,F,\;\,G\) thì khả năng xảy ra biến cố \(E\) là thấp nhất.
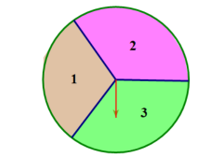
Một tấm bìa hình tròn được chia thành 3 hình quạt bằng nhau và được đánh số \(1;\;\,2;\;\,3\) (như hình vẽ). Xoay tấm bìa quanh tâm hình tròn hai lần và xem tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Tính xác suất của biến cố \(N:\) “Tổng số ghi được ở 2 lần quay không lớn hơn 4” (Kết quả ghi dưới dạng số thập phân, làm tròn kết quả đến hàng phần mười).
Một nhóm 40 người gồm 8 ông, 10 bà, 12 em gái và 10 em trai. Chọn ngẫu nhiên một người trong nhóm, tính xác suất để người được chọn có giới tính nữ. (Kết quả ghi dưới dạng số thập phân)
Trong túi đựng 50 viên kẹo giống hệt nhau, có hai màu vàng và hồng. Lấy ngẫu nhiên một viên kẹo từ túi đựng. Xét các biến cố:
\(A:\) “Lấy được viên kẹo màu hồng”; \(B:\) “Lấy được viên kẹo màu vàng”.
Biết rằng, \(P\left( A \right) = \frac{2}{3}P\left( B \right).\) Hỏi trong túi đựng có bao nhiêu viên kẹo màu hồng?
Một hộp đựng 35 viên bi có cùng kích thước và khối lượng với hai màu xanh và đen, trong đó số viên bi xanh gấp 4 lần số viên bi màu đen. Bình lấy ngẫu nhiên một viên bi trong hộp. Tính xác suất để Bình lấy được viên bi màu xanh. (Kết quả ghi dưới dạng số thập phân)
Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của biến cố “Số tự nhiên được viết ra là bội của 10”. (Kết quả ghi dưới dạng số thập phân)
