20 câu trắc nghiệm Toán 8 Cánh diều Ôn tập chương IV (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Cho các hình dưới đây.

Hình có dạng là hình chóp tam giác đều là
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Các mặt bên của hình chóp tam giác đều là hình gì?
Tam giác đều.
Tam giác nhọn.
Tam giác cân.
Tam giác vuông.
Cho hình chóp tứ giác đều \(S.ABCD\) như hình vẽ trên.
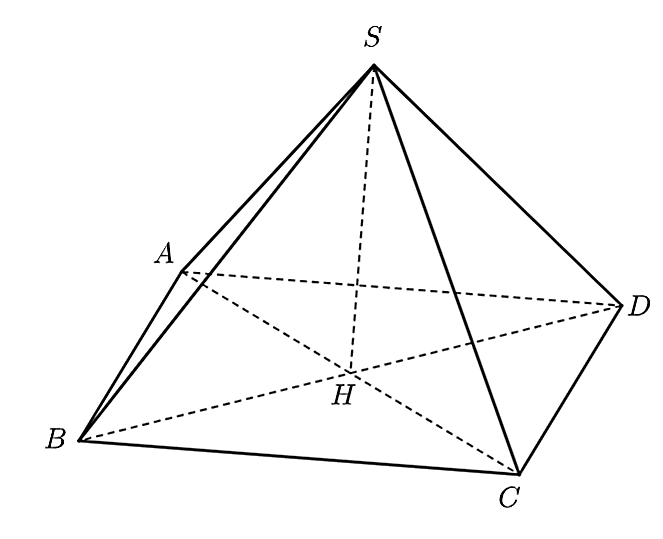
Khi đó, \(SH\) được gọi là
đường cao.
cạnh bên.
cạnh đáy.
đường chéo.
Hình chóp tam giác đều có
4 mặt, 4 cạnh.
6 mặt, 4 cạnh.
4 mặt, 6 cạnh.
6 mặt, 6 cạnh.
Diện tích xung quanh của hình chóp tứ giác đều là \({S_{xq}} = p.d\). Trong đó \(d\) là gì?
Chiều cao.
Trung đoạn.
Nửa chu vi đáy.
Cạnh đáy.
Thể tích của hình chóp là
tích nửa chu vi đáy và đường cao của hình chóp.
tích nửa chu vi đáy và trung đoạn.
một phần ba tích diện tích đáy và chiều cao.
một phần b tích diện tích đáy và trung đoạn.
Diện tích xung quanh của hình chóp tam giác đều là
Nửa chu vi đáy nhân với đường cao.
Chu vi đáy nhân với trung đoạn.
Nửa chu vi đáy nhân với trung đoạn.
Chu vi đáy nhân với chiều cao.
Cho các miếng bìa sau.

Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đường cao của hình chóp tam giác đều là
Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy.
Đoạn thẳng nối đỉnh của hình chóp và trung điểm của một cạnh đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm tùy ý nằm trong mặt đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm bất kì trên cạnh bên của hình chóp.
Một hình chóp tứ giác đều có diện tích đáy bằng \(30\,\;{\rm{c}}{{\rm{m}}^2}\) và chiều cao bằng \(5\;\,{\rm{cm}}{\rm{.}}\) Thể tích hình chóp tứ giác đều đó bằng
\(150\,\;{\rm{c}}{{\rm{m}}^2}.\)
\(150\;\,{\rm{c}}{{\rm{m}}^3}.\)
\(50\;\,{\rm{c}}{{\rm{m}}^3}.\)
\(50\;\,{\rm{c}}{{\rm{m}}^2}.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)
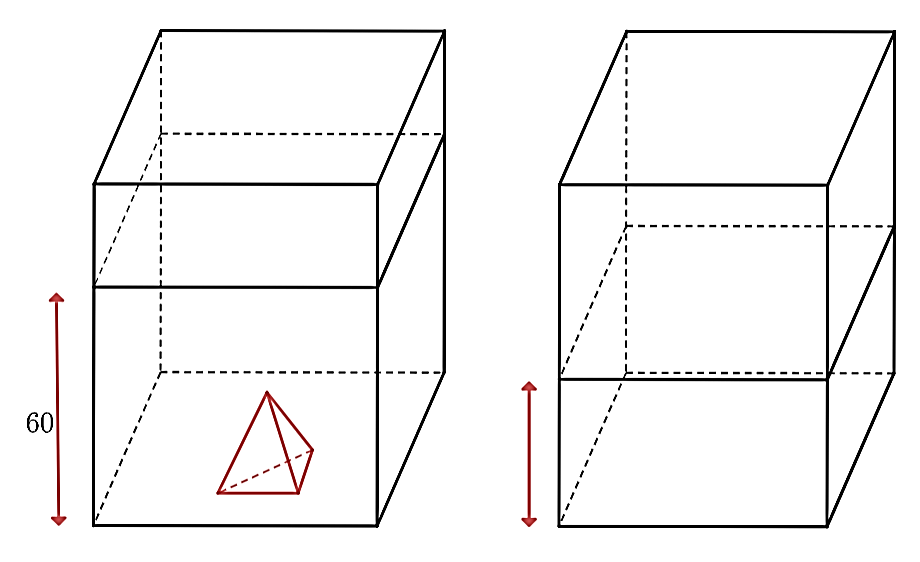
Khi đó,
a) Thể tích khối chóp tam giác đều là \(2{\rm{ }}700{\rm{ c}}{{\rm{m}}^3}.\)
b) Thể tích lượng nước đổ vào là \(108{\rm{ 000}}\,\,{\rm{c}}{{\rm{m}}^3}.\)
c) Diện tích đáy của bể là \(180{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
d) Khi khối đá được lấy ra thì mực nước của bể lớn hơn 58 m.
Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm,}}\) chiều cao \({\rm{2,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\)
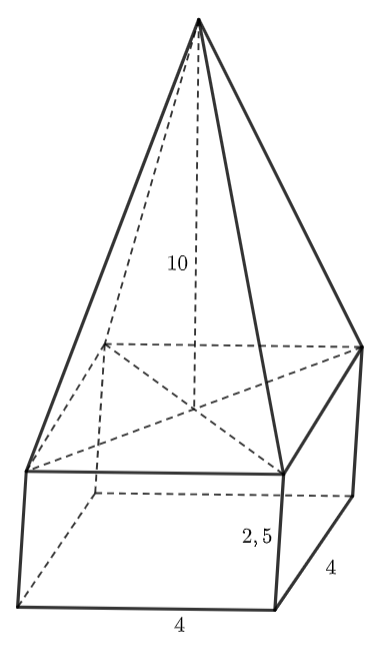
Khi đó,
a) Thể tích phần khối bê tông dạng hình hộp chữ nhật là \(40{\rm{ d}}{{\rm{m}}^{\rm{3}}}.\)
b) Thể tích phần khối bê tông dạng hình chóp lớn hơn \(50{\rm{ d}}{{\rm{m}}^{\rm{3}}}.\)
c) Tỉ lệ thể tích khối bê tông dạng hình hộp chữ nhật so với khối bê tông hình chóp là \(\frac{3}{4}.\)
d) Thể tích cả khối bê tông lớn hơn \(95{\rm{ d}}{{\rm{m}}^{\rm{3}}}.\)
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (được minh họa bằng hình chóp \(S.ABC\) có \(H\) là trung điểm \(AB\) và \(G\) là trọng tâm mặt đáy. ).
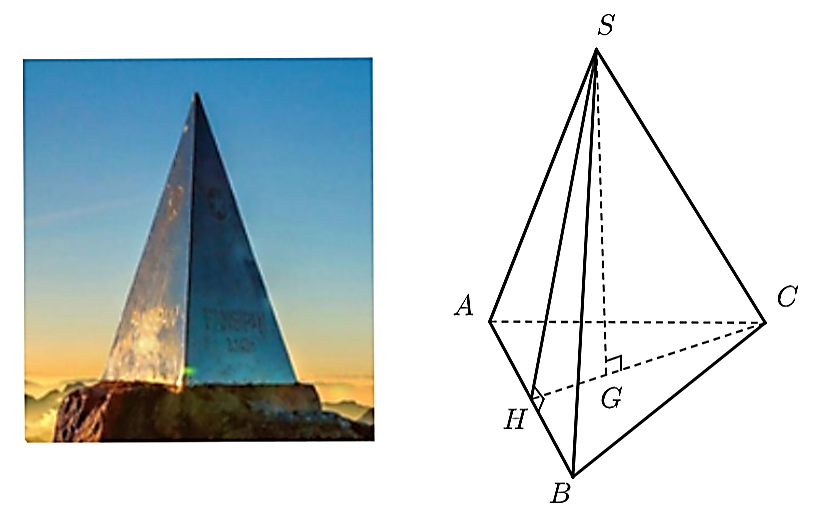
a) \(HA = HB = 30{\rm{ cm}}{\rm{.}}\)
b) \(CH = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
c) \(SH = 30\sqrt 3 {\rm{ cm}}{\rm{.}}\)
d) Diện tích xung quanh của hình chóp lớn hơn \(8\,530\,\,{{\rm{m}}^2}.\)
Một khối gỗ (như hình vẽ) gồm đế là hình lập phương có cạnh \(18\;\,{\rm{cm}}\) và phần trên là một hình chóp tứ giác đều:
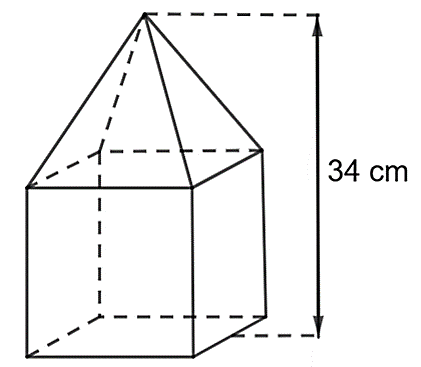
a)Chiều cao của hình chóp tứ giác đều bằng \(16\;\,{\rm{cm}}{\rm{.}}\)
b)Thể tích đế khối gỗ là \(5\;\,832\;\,{\rm{c}}{{\rm{m}}^3}.\)
c)Thể tích phần trên của khối gỗ là \(1\;\,728\;\;{\rm{c}}{{\rm{m}}^3}.\)
d)Thể tích của khối gỗ nhỏ hơn \(7\;\,{\rm{d}}{{\rm{m}}^3}.\)
Cho hình chóp tam giác đều \(S.ABC\) như hình vẽ:
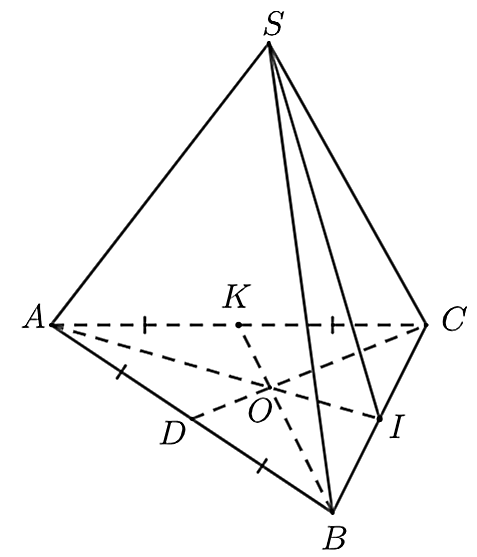
Biết rằng \(AB = 12\;{\rm{cm,}}\;\,SI = \frac{4}{3}AB.\) Khi đó:
a)\(O\) là trọng tâm của tam giác \(ABC.\)
b)\(I\) là trung điểm của \(BC.\)
c)\(SI\) là chiều cao hình chóp \(S.ABC.\)
d)Diện tích xung quanh của hình chóp \(S.ABC\) bằng \(144\;{\rm{c}}{{\rm{m}}^2}.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Một hình chóp tam giác đều có thể tích là \({V_1}.\) Nếu tăng chiều cao của hình chóp đó lên 3 lần và giữ nguyên độ dài cạnh của tam giác đáy thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)
Một hình chóp tứ giác đều có thể tích là \({V_1}.\) Nếu giữ nguyên chiều cao của hình chóp đó và tăng độ dài cạnh đáy lên 5 lần thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)
Một chiếc gàu có dạng hình chóp tam giác đều và một chiếc bình có dạng hình lăng trụ đứng tam giác có cùng diện tích đáy. Người ta đổ 15 gàu nước vào bình và đo được mực nước trong bình tăng thêm \(2,5\,\;{\rm{m}}{\rm{.}}\) Hỏi chiều cao của chiếc gàu đó bằng bao nhiêu \({\rm{m?}}\)
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao \(21{\rm{ m,}}\) độ dài cạnh đáy là \(34{\rm{ m}}\).

Tính tổng diện tích của các tấm kính để phủ kín bốn mặt bên của bảo tàng này (đơn vị: m2).
(Các kết quả làm tròn đến hàng đơn vị)
Nhà bạn thu có một đèn trang trí có dạng hình chóp tam giác đều như hình bẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng \(20{\rm{ cm}}\). Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.
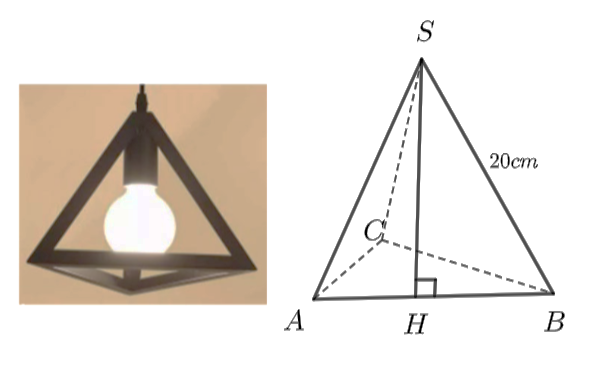
Tính diện tích giấy màu mà bạn Thu sử dụng (đơn vị: cm2, coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
